Banach lattice

A vector lattice that is at the same time a Banach space with a norm which satisfies the monotonicity condition:

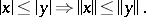A Banach lattice is also called a KB-lineal, whereas an arbitrary normed lattice, i.e. a vector lattice with a monotone norm, is called a KN-lineal. When completing a normed lattice in norm, the order relations may be extended to the resulting Banach space so that it becomes a Banach lattice. If it is possible to introduce in a lattice a Banach topology which converts it to a Banach lattice, such a topology is unique. The simplest example of a Banach lattice is the space 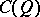of continuous functions on an arbitrary compact topological space 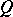with the natural (pointwise) order and with the ordinary (uniform) norm. Other examples of Banach lattices include 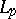spaces and Orlicz spaces (cf. Orlicz space). In Banach lattices convergence in norm is ()-convergence for convergence with a regulator. This is not true of normed lattices.

An important special case is a Banach lattice of bounded elements. If a lattice 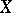contains a strong unit 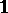, i.e. if for each 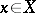there exists a 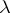such that 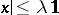, then the smallest 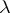for which this inequality is valid is taken as . The normed lattice thus obtained is called a normed lattice of bounded elements; if it is complete in norm, it is called a Banach lattice of bounded elements. In a Banach lattice (and even in a normed lattice) of bounded elements convergence in norm is identical with convergence with a regulator, while the boundedness of a set of elements in norm is identical with order boundedness. If a normed lattice of bounded elements is conditionally 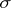-complete, it is complete in norm.

The space 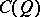is a Banach lattice of bounded elements in which the function 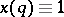is taken as the unit. For any Banach lattice 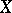of bounded elements there exists a compact Hausdorff space 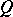such that is algebraically and lattice isomorphic to the space 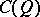. This is an abstract characterization of the Banach lattice of continuous functions on a compact Hausdorff space.

In any normed lattice an additive functional that is continuous in norm is regular and, moreover, is representable as the difference of two additive functionals which are continuous in norm. In a Banach lattice each positive additive functional is continuous in norm, which means that the classes of regular functionals and additive functionals which are continuous in norm coincide. The space 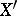which is dual in the sense of Banach to the normed lattice is a conditionally complete Banach lattice. In a normed lattice the Hahn–Banach theorem may be strengthened as follows: For any 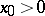there exists a positive additive functional , which is continuous in norm, such that , .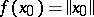

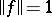References

[1]	B.Z. Vulikh, "Introduction to the theory of partially ordered spaces" , Wolters-Noordhoff (1967) (Translated from Russian)
[2]	M.M. Day, "Normed linear spaces" , Springer (1958)

Comments

Cf. Riesz space for the notion of "convergence with a regulator" . The terminology in the article above is from [1], and is not in general use in the Western literature.

A vector lattice (i.e. a real linear (partially) ordered vector space that is at the same time a lattice) is usually called a Riesz space. A norm 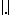on a Riesz space 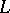is called a Riesz norm if

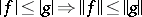whenever 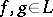(called the monotonicity condition, above). Here

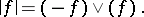A normed Riesz space is understood to mean a Riesz space provided with a Riesz norm. The definition of a Banach lattice can now be rephrased as follows: A Banach lattice is a normed Riesz space that is complete in the norm.

All (Riesz) norms on a Banach lattice are equivalent.

For a Banach lattice 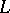the order dual space (cf. Riesz space) and norm dual space coincide (this is not true for normed Riesz spaces in general). A Banach lattice, required to be complete in norm, need not be Dedekind complete. However, any Banach lattice 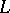(even, every normed Riesz space) can be regarded as a (Riesz) subspace of a Dedekind-complete Banach lattice (the bi-dual (in norm) of 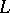, cf. Banach space).

References

[a1]	H.H. Schaefer, "Banach lattices and positive operators" , Springer (1974)
[a2]	W.A.J. Luxemburg, A.C. Zaanen, "Riesz spaces" , I , North-Holland (1971)
[a3]	J. Lindenstrauss, L. Tzafriri, "Classical Banach spaces" , 2 , Springer (1979)
[a4]	A.C. Zaanen, "Riesz spaces" , II , North-Holland (1983)