Difference between revisions of "Kodaira theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | k0556401.png | ||
| + | $#A+1 = 31 n = 1 | ||
| + | $#C+1 = 31 : ~/encyclopedia/old_files/data/K055/K.0505640 Kodaira theorem, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''Kodaira's vanishing theorem'' | ''Kodaira's vanishing theorem'' | ||
| − | A theorem on the vanishing of the cohomology groups | + | A theorem on the vanishing of the cohomology groups $ H ^ {i} ( X, {\mathcal O} ( L) ) $, |
| + | $ i < \mathop{\rm dim} X $, | ||
| + | where $ {\mathcal O} ( L) $ | ||
| + | is the sheaf of holomorphic sections of the [[Negative vector bundle|negative vector bundle]] $ L $ | ||
| + | of rank $ 1 $ | ||
| + | on a compact [[Complex manifold|complex manifold]] $ X $. | ||
| + | An equivalent statement of Kodaira's vanishing theorem is that | ||
| − | + | $$ | |
| + | H ^ {i} ( X, {\mathcal O} ( L \otimes K _ {X} ) ) = 0 ,\ \ | ||
| + | i > 0 , | ||
| + | $$ | ||
| − | for any [[Positive vector bundle|positive vector bundle]] of rank 1 (here | + | for any [[Positive vector bundle|positive vector bundle]] of rank 1 (here $ K _ {X} $ |
| + | denotes the canonical line bundle on $ X $). | ||
| + | In terms of divisors (cf. [[Divisor|Divisor]]) Kodaira's vanishing theorem is stated as the equation $ H ^ {i} ( X , {\mathcal O} _ {X} ( - D ) ) = 0 $ | ||
| + | for $ i < \mathop{\rm dim} X $ | ||
| + | and any divisor $ D $ | ||
| + | such that for some $ n \geq 1 $, | ||
| + | $ n D $ | ||
| + | is a hyperplane section in some projective imbedding of $ X $. | ||
The theorem was proved by transcendental methods by K. Kodaira [[#References|[1]]] (see also [[#References|[2]]]) as a generalization to arbitrary dimension of the classical theorem on the regularity of an adjoint system on an algebraic surface. There exists an example of a normal algebraic surface over a field of positive characteristic for which Kodaira's vanishing theorem is false [[#References|[4]]]. | The theorem was proved by transcendental methods by K. Kodaira [[#References|[1]]] (see also [[#References|[2]]]) as a generalization to arbitrary dimension of the classical theorem on the regularity of an adjoint system on an algebraic surface. There exists an example of a normal algebraic surface over a field of positive characteristic for which Kodaira's vanishing theorem is false [[#References|[4]]]. | ||
| Line 11: | Line 39: | ||
Kodaira's theorem also holds for holomorphic vector bundles of arbitrary rank that are negative in the sense of J. Nakano. The following result is also a generalization of Kodaira's theorem: | Kodaira's theorem also holds for holomorphic vector bundles of arbitrary rank that are negative in the sense of J. Nakano. The following result is also a generalization of Kodaira's theorem: | ||
| − | + | $$ | |
| + | H ^ {i} ( X , \Omega ^ {p} ( L) ) = 0 \ \ | ||
| + | \textrm{ for } \ | ||
| + | p + i \geq \mathop{\rm dim} X + r , | ||
| + | $$ | ||
| − | where | + | where $ L $ |
| + | is a weakly-positive vector bundle of rank $ r $ | ||
| + | on the compact complex manifold $ X $, | ||
| + | and $ \Omega ^ {p} ( L) = \Omega ^ {p} \otimes {\mathcal O} ( L) $ | ||
| + | is the sheaf of holomorphic forms (cf. [[Holomorphic form|Holomorphic form]]) of degree $ p $ | ||
| + | with values in $ L $. | ||
| + | For weakly-negative vector bundles $ L $, | ||
| + | vanishing takes place when $ p + i \leq \mathop{\rm dim} X - r $. | ||
| + | Analogues of these theorems have been obtained for weakly-complete manifolds $ X $, | ||
| + | that is, manifolds admitting a smooth [[Pluriharmonic function|pluriharmonic function]] $ \psi $ | ||
| + | such that the set $ \{ {x \in X } : {\psi ( x) < c } \} $ | ||
| + | is relatively compact in $ X $ | ||
| + | for all $ c \in \mathbf R $, | ||
| + | and for compact complex spaces $ X $ | ||
| + | having $ n = \mathop{\rm dim} X $ | ||
| + | algebraically-independent meromorphic functions [[#References|[5]]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> K. Kodaira, "On a differential geometric method in the theory of analytic stacks" ''Proc. Nat. Acad. Sci. USA'' , '''39''' (1953) pp. 1268–1273 {{MR|0066693}} {{ZBL|0053.11701}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) {{MR|0608414}} {{ZBL|0435.32004}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D. Mumford, "Pathologies III" ''Amer. J. Math.'' , '''89''' : 1 (1967) pp. 94–104 {{MR|0217091}} {{ZBL|0146.42403}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> O. Zariski, "Algebraic surfaces" , Springer (1971) {{MR|0469915}} {{ZBL|0219.14020}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A.L. Onishchik, "Pseudoconvexity in the theory of complex spaces" ''J. Soviet Math.'' , '''14''' : 4 (1980) pp. 1363–1407 ''Itogi Nauk. Algebra Topol. Geom.'' , '''15''' (1977) pp. 93–171 {{MR|}} {{ZBL|0449.32020}} </TD></TR></table> |
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| Line 26: | Line 71: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Raynaud, "Contre-example du "vanishing theorem" en caractéristique <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055640/k05564032.png" />" K.G. Ramanathan (ed.) , ''C.P. Ramanujam, a tribute'' , Springer (1978) pp. 273–278</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> E. Viehweg, "Vanishing theorems and positivity in algebraic fibre spaces" , ''Proc. Internat. Congress Mathematicians (Berkeley, 1986)'' , '''1''' , Amer. Math. Soc. (1987) pp. 682–688 {{MR|0934270}} {{ZBL|0685.14013}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Kollar, "Vanishing theorems for cohomology groups" S.J. Bloch (ed.) , ''Algebraic geometry (Bowdoin, 1985)'' , ''Proc. Symp. Pure Math.'' , '''46''' : 2 , Amer. Math. Soc. (1987) pp. 233–243 {{MR|0927959}} {{ZBL|0658.14012}} </TD></TR></table> |
Latest revision as of 22:14, 5 June 2020
Kodaira's vanishing theorem
A theorem on the vanishing of the cohomology groups $ H ^ {i} ( X, {\mathcal O} ( L) ) $, $ i < \mathop{\rm dim} X $, where $ {\mathcal O} ( L) $ is the sheaf of holomorphic sections of the negative vector bundle $ L $ of rank $ 1 $ on a compact complex manifold $ X $. An equivalent statement of Kodaira's vanishing theorem is that
$$ H ^ {i} ( X, {\mathcal O} ( L \otimes K _ {X} ) ) = 0 ,\ \ i > 0 , $$
for any positive vector bundle of rank 1 (here $ K _ {X} $ denotes the canonical line bundle on $ X $). In terms of divisors (cf. Divisor) Kodaira's vanishing theorem is stated as the equation $ H ^ {i} ( X , {\mathcal O} _ {X} ( - D ) ) = 0 $ for $ i < \mathop{\rm dim} X $ and any divisor $ D $ such that for some $ n \geq 1 $, $ n D $ is a hyperplane section in some projective imbedding of $ X $.
The theorem was proved by transcendental methods by K. Kodaira [1] (see also [2]) as a generalization to arbitrary dimension of the classical theorem on the regularity of an adjoint system on an algebraic surface. There exists an example of a normal algebraic surface over a field of positive characteristic for which Kodaira's vanishing theorem is false [4].
Kodaira's theorem also holds for holomorphic vector bundles of arbitrary rank that are negative in the sense of J. Nakano. The following result is also a generalization of Kodaira's theorem:
$$ H ^ {i} ( X , \Omega ^ {p} ( L) ) = 0 \ \ \textrm{ for } \ p + i \geq \mathop{\rm dim} X + r , $$
where $ L $ is a weakly-positive vector bundle of rank $ r $ on the compact complex manifold $ X $, and $ \Omega ^ {p} ( L) = \Omega ^ {p} \otimes {\mathcal O} ( L) $ is the sheaf of holomorphic forms (cf. Holomorphic form) of degree $ p $ with values in $ L $. For weakly-negative vector bundles $ L $, vanishing takes place when $ p + i \leq \mathop{\rm dim} X - r $. Analogues of these theorems have been obtained for weakly-complete manifolds $ X $, that is, manifolds admitting a smooth pluriharmonic function $ \psi $ such that the set $ \{ {x \in X } : {\psi ( x) < c } \} $ is relatively compact in $ X $ for all $ c \in \mathbf R $, and for compact complex spaces $ X $ having $ n = \mathop{\rm dim} X $ algebraically-independent meromorphic functions [5].
References
| [1] | K. Kodaira, "On a differential geometric method in the theory of analytic stacks" Proc. Nat. Acad. Sci. USA , 39 (1953) pp. 1268–1273 MR0066693 Zbl 0053.11701 |
| [2] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) MR0608414 Zbl 0435.32004 |
| [3] | D. Mumford, "Pathologies III" Amer. J. Math. , 89 : 1 (1967) pp. 94–104 MR0217091 Zbl 0146.42403 |
| [4] | O. Zariski, "Algebraic surfaces" , Springer (1971) MR0469915 Zbl 0219.14020 |
| [5] | A.L. Onishchik, "Pseudoconvexity in the theory of complex spaces" J. Soviet Math. , 14 : 4 (1980) pp. 1363–1407 Itogi Nauk. Algebra Topol. Geom. , 15 (1977) pp. 93–171 Zbl 0449.32020 |
Comments
Counterexamples to Kodaira's theorem for non-singular varieties over a field of positive characteristic were given by M. Raynaud [a1]. There exists a much stronger version of Kodaira's theorem, due to E. Viehweg and Y. Kawamata [a2].
Recently, many generalizations of Kodaira vanishing have been found, see [a3].
References
| [a1] | M. Raynaud, "Contre-example du "vanishing theorem" en caractéristique 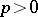 " K.G. Ramanathan (ed.) , C.P. Ramanujam, a tribute , Springer (1978) pp. 273–278 " K.G. Ramanathan (ed.) , C.P. Ramanujam, a tribute , Springer (1978) pp. 273–278 |
| [a2] | E. Viehweg, "Vanishing theorems and positivity in algebraic fibre spaces" , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , 1 , Amer. Math. Soc. (1987) pp. 682–688 MR0934270 Zbl 0685.14013 |
| [a3] | J. Kollar, "Vanishing theorems for cohomology groups" S.J. Bloch (ed.) , Algebraic geometry (Bowdoin, 1985) , Proc. Symp. Pure Math. , 46 : 2 , Amer. Math. Soc. (1987) pp. 233–243 MR0927959 Zbl 0658.14012 |
Kodaira theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kodaira_theorem&oldid=13756