Difference between revisions of "Hopf manifold"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | A | + | <!-- |
| + | h1102701.png | ||
| + | $#A+1 = 29 n = 1 | ||
| + | $#C+1 = 29 : ~/encyclopedia/old_files/data/H110/H.1100270 Hopf manifold | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | A complex Hopf manifold is a quotient of $ \mathbf C ^ {n} \setminus \{ 0 \} $ | ||
| + | by the infinite [[Cyclic group|cyclic group]] of holomorphic transformations generated by $ z \mapsto \lambda z $, | ||
| + | $ \lambda \in \mathbf C \setminus \{ 0 \} $, | ||
| + | $ | \lambda | \neq 1 $. | ||
| + | It is usually denoted by $ \mathbf C H _ \lambda ^ {n} $. | ||
| + | As a [[Differentiable manifold|differentiable manifold]], any $ \mathbf C H _ \lambda ^ {n} $ | ||
| + | is diffeomorphic to $ S ^ {2n - 1 } \times S ^ {1} $. | ||
| + | Consequently, when $ n \geq 2 $ | ||
| + | the first [[Betti number|Betti number]] $ b _ {1} ( \mathbf C H _ \lambda ^ {n} ) = 1 $; | ||
| + | hence, such $ \mathbf C H _ \lambda ^ {n} $ | ||
| + | provide examples of compact complex manifolds (cf. [[Complex manifold|Complex manifold]]) not admitting any [[Kähler metric|Kähler metric]] (note that, for $ n = 1 $, | ||
| + | $ \mathbf C H _ \lambda ^ {1} $ | ||
| + | is a $ 1 $- | ||
| + | dimensional [[Complex torus|complex torus]]). However, these manifolds do carry a particularly interesting class of Hermitian metrics (cf. [[Hermitian metric|Hermitian metric]]), namely locally conformal Kähler metrics (a Hermitian metric is locally conformal Kähler if its fundamental $ 2 $- | ||
| + | form $ \Omega $ | ||
| + | satisfies the integrability condition $ d \Omega = \omega \wedge \Omega $ | ||
| + | with a closed $ 1 $- | ||
| + | form $ \omega $, | ||
| + | called the Lee form). An example of such a metric is the projection of the following metric on $ \mathbf C ^ {n} \setminus \{ 0 \} $: | ||
| + | $ g _ {0} = | z | ^ {- 2 } \delta _ {jk } dz ^ {j} \otimes d {\overline{z}\; } ^ {k} $, | ||
| + | whose Lee form is $ \omega _ {0} = | z | ^ {- 2 } \sum ( z ^ {j} d {\overline{z}\; } ^ {j} + {\overline{z}\; } ^ {j} dz ^ {j} ) $. | ||
| + | It is parallel with respect to the [[Levi-Civita connection|Levi-Civita connection]] of $ g _ {0} $. | ||
| + | This originated the study of the more general class of generalized Hopf manifolds: locally conformal Kähler manifolds with parallel Lee form. Their geometry is closely related to Sasakian and Kählerian geometries. Generically, a compact generalized Hopf manifold arises as the total space of a flat, principal $ S ^ {1} $ | ||
| + | bundle over a compact Sasakian orbifold and, on the other hand, fibres into $ 1 $- | ||
| + | dimensional complex tori over a Kähler orbifold. | ||
I. Vaisman conjectured that a compact locally conformal Kähler manifold that is not globally conformal Kähler must have an odd Betti number. To date (1996), this has only been proved for generalized Hopf manifolds (see [[#References|[a5]]]). | I. Vaisman conjectured that a compact locally conformal Kähler manifold that is not globally conformal Kähler must have an odd Betti number. To date (1996), this has only been proved for generalized Hopf manifolds (see [[#References|[a5]]]). | ||
| − | It is rather difficult to characterize the Hopf manifolds among the locally conformal Kähler manifolds. However, in complex dimension | + | It is rather difficult to characterize the Hopf manifolds among the locally conformal Kähler manifolds. However, in complex dimension $ 2 $ |
| + | several such characterizations are available; for instance, the only compact complex surface with $ b _ {1} = 1 $ | ||
| + | and admitting conformally flat Hermitian metrics is $ \mathbf C H _ \lambda ^ {2} $( | ||
| + | cf. [[#References|[a4]]]; see also [[#References|[a1]]]). | ||
| − | By analogy, "real Hopf manifoldreal Hopf manifolds" were defined as (compact) quotients of | + | By analogy, "real Hopf manifoldreal Hopf manifolds" were defined as (compact) quotients of $ \mathbf R ^ {n} \setminus \{ 0 \} $ |
| + | by an appropriate group of conformal transformations (see [[#References|[a6]]] and [[#References|[a2]]]). Similarly, "quaternion Hopf manifoldquaternion Hopf manifolds" are defined as quotients of $ \mathbf H ^ {n} \setminus \{ 0 \} $( | ||
| + | see [[#References|[a3]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C.P. Boyer, "Conformal duality and compact complex surfaces" ''Math. Ann.'' , '''274''' (1986) pp. 517–526</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Gauduchon, "Structures de Weyl–Einstein, espaces de twisteurs et variétés de type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110270/h11027030.png" />" ''J. Reine Angew. Math.'' , '''455''' (1995) pp. 1–50</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> L. Ornea, P. Piccinni, "Locally conformal Kähler structures in quaternionic geometry" ''Trans. Amer. Math. Soc.'' , '''349''' (1997) pp. 641–655</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Pontecorvo, "Uniformization of conformally flat Hermitian surfaces" ''Diff. Geom. Appl.'' , '''3''' (1992) pp. 295–305</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> I. Vaisman, "Generalized Hopf manifolds" ''Geom. Dedicata'' , '''13''' (1982) pp. 231–255</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> I. Vaisman, C. Reischer, "Local similarity manifolds" ''Ann. Mat. Pura Appl.'' , '''35''' (1983) pp. 279–292</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> S. Dragomir, L. Ornea, "Locally conformal Kähler geometry" , Birkhäuser (1997)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C.P. Boyer, "Conformal duality and compact complex surfaces" ''Math. Ann.'' , '''274''' (1986) pp. 517–526</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Gauduchon, "Structures de Weyl–Einstein, espaces de twisteurs et variétés de type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110270/h11027030.png" />" ''J. Reine Angew. Math.'' , '''455''' (1995) pp. 1–50</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> L. Ornea, P. Piccinni, "Locally conformal Kähler structures in quaternionic geometry" ''Trans. Amer. Math. Soc.'' , '''349''' (1997) pp. 641–655</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Pontecorvo, "Uniformization of conformally flat Hermitian surfaces" ''Diff. Geom. Appl.'' , '''3''' (1992) pp. 295–305</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> I. Vaisman, "Generalized Hopf manifolds" ''Geom. Dedicata'' , '''13''' (1982) pp. 231–255</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> I. Vaisman, C. Reischer, "Local similarity manifolds" ''Ann. Mat. Pura Appl.'' , '''35''' (1983) pp. 279–292</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> S. Dragomir, L. Ornea, "Locally conformal Kähler geometry" , Birkhäuser (1997)</TD></TR></table> | ||
Latest revision as of 22:11, 5 June 2020
A complex Hopf manifold is a quotient of $ \mathbf C ^ {n} \setminus \{ 0 \} $
by the infinite cyclic group of holomorphic transformations generated by $ z \mapsto \lambda z $,
$ \lambda \in \mathbf C \setminus \{ 0 \} $,
$ | \lambda | \neq 1 $.
It is usually denoted by $ \mathbf C H _ \lambda ^ {n} $.
As a differentiable manifold, any $ \mathbf C H _ \lambda ^ {n} $
is diffeomorphic to $ S ^ {2n - 1 } \times S ^ {1} $.
Consequently, when $ n \geq 2 $
the first Betti number $ b _ {1} ( \mathbf C H _ \lambda ^ {n} ) = 1 $;
hence, such $ \mathbf C H _ \lambda ^ {n} $
provide examples of compact complex manifolds (cf. Complex manifold) not admitting any Kähler metric (note that, for $ n = 1 $,
$ \mathbf C H _ \lambda ^ {1} $
is a $ 1 $-
dimensional complex torus). However, these manifolds do carry a particularly interesting class of Hermitian metrics (cf. Hermitian metric), namely locally conformal Kähler metrics (a Hermitian metric is locally conformal Kähler if its fundamental $ 2 $-
form $ \Omega $
satisfies the integrability condition $ d \Omega = \omega \wedge \Omega $
with a closed $ 1 $-
form $ \omega $,
called the Lee form). An example of such a metric is the projection of the following metric on $ \mathbf C ^ {n} \setminus \{ 0 \} $:
$ g _ {0} = | z | ^ {- 2 } \delta _ {jk } dz ^ {j} \otimes d {\overline{z}\; } ^ {k} $,
whose Lee form is $ \omega _ {0} = | z | ^ {- 2 } \sum ( z ^ {j} d {\overline{z}\; } ^ {j} + {\overline{z}\; } ^ {j} dz ^ {j} ) $.
It is parallel with respect to the Levi-Civita connection of $ g _ {0} $.
This originated the study of the more general class of generalized Hopf manifolds: locally conformal Kähler manifolds with parallel Lee form. Their geometry is closely related to Sasakian and Kählerian geometries. Generically, a compact generalized Hopf manifold arises as the total space of a flat, principal $ S ^ {1} $
bundle over a compact Sasakian orbifold and, on the other hand, fibres into $ 1 $-
dimensional complex tori over a Kähler orbifold.
I. Vaisman conjectured that a compact locally conformal Kähler manifold that is not globally conformal Kähler must have an odd Betti number. To date (1996), this has only been proved for generalized Hopf manifolds (see [a5]).
It is rather difficult to characterize the Hopf manifolds among the locally conformal Kähler manifolds. However, in complex dimension $ 2 $ several such characterizations are available; for instance, the only compact complex surface with $ b _ {1} = 1 $ and admitting conformally flat Hermitian metrics is $ \mathbf C H _ \lambda ^ {2} $( cf. [a4]; see also [a1]).
By analogy, "real Hopf manifoldreal Hopf manifolds" were defined as (compact) quotients of $ \mathbf R ^ {n} \setminus \{ 0 \} $ by an appropriate group of conformal transformations (see [a6] and [a2]). Similarly, "quaternion Hopf manifoldquaternion Hopf manifolds" are defined as quotients of $ \mathbf H ^ {n} \setminus \{ 0 \} $( see [a3]).
References
| [a1] | C.P. Boyer, "Conformal duality and compact complex surfaces" Math. Ann. , 274 (1986) pp. 517–526 |
| [a2] | P. Gauduchon, "Structures de Weyl–Einstein, espaces de twisteurs et variétés de type 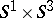 " J. Reine Angew. Math. , 455 (1995) pp. 1–50 " J. Reine Angew. Math. , 455 (1995) pp. 1–50 |
| [a3] | L. Ornea, P. Piccinni, "Locally conformal Kähler structures in quaternionic geometry" Trans. Amer. Math. Soc. , 349 (1997) pp. 641–655 |
| [a4] | M. Pontecorvo, "Uniformization of conformally flat Hermitian surfaces" Diff. Geom. Appl. , 3 (1992) pp. 295–305 |
| [a5] | I. Vaisman, "Generalized Hopf manifolds" Geom. Dedicata , 13 (1982) pp. 231–255 |
| [a6] | I. Vaisman, C. Reischer, "Local similarity manifolds" Ann. Mat. Pura Appl. , 35 (1983) pp. 279–292 |
| [a7] | S. Dragomir, L. Ornea, "Locally conformal Kähler geometry" , Birkhäuser (1997) |
Hopf manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hopf_manifold&oldid=18689