Difference between revisions of "Crystallographic group"
(Remove spurious bold italic markup) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | c0271901.png | ||
| + | $#A+1 = 108 n = 2 | ||
| + | $#C+1 = 108 : ~/encyclopedia/old_files/data/C027/C.0207190 Crystallographic group | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A discrete group of motions of an $ n $- | |
| + | dimensional Euclidean space $ E ^ {n} $ | ||
| + | having a bounded [[Fundamental domain|fundamental domain]]. Two crystallographic groups are said to be equivalent if they are conjugate in the group of affine transformations of $ E ^ {n} $. | ||
| + | |||
| + | The origin of the theory of crystallographic groups is connected with the study of the symmetry of ornaments $ ( n = 2) $ | ||
| + | and the structure of crystals $ ( n = 3) $. | ||
| + | A classification of all planar (two-dimensional) and spatial (three-dimensional) crystallographic groups was achieved at the end of the 19th century by E.S. Fedorov and somewhat later by A. Schoenflies (see [[#References|[2]]], [[#References|[3]]], and also [[#References|[6]]], [[#References|[7]]], [[#References|[9]]]). Up to equivalence, there are 17 planar and 219 spatial crystallographic groups; if, however, the spatial groups are considered up to conjugacy with respect to orientation-preserving affine transformations, their number is 230. In 1910, L. Bieberbach investigated crystallographic groups of arbitrary dimension . In particular, he proved the following theorems: | ||
| + | |||
| + | 1) Any $ n $- | ||
| + | dimensional crystallographic group $ \Gamma $ | ||
| + | contains $ n $ | ||
| + | linearly independent parallel translations; the group $ G $ | ||
| + | of linear parts of the transformations from $ \Gamma $ | ||
| + | is finite. (For $ n = 3 $ | ||
| + | this was proved in [[#References|[3]]].) | ||
2) Two crystallographic groups are equivalent if and only if they are isomorphic as abstract groups. | 2) Two crystallographic groups are equivalent if and only if they are isomorphic as abstract groups. | ||
| − | 3) For any | + | 3) For any $ n $, |
| + | there are — up to equivalence — only finitely many $ n $- | ||
| + | dimensional crystallographic groups (this is a solution to Hilbert's 18th problem). | ||
| − | Theorem 1 yields the following description of the structure of crystallographic groups as abstract groups. Let | + | Theorem 1 yields the following description of the structure of crystallographic groups as abstract groups. Let $ L $ |
| + | be the set of all parallel translations in a crystallographic group $ \Gamma $. | ||
| + | Then $ L $ | ||
| + | is a normal subgroup of finite index, isomorphic to $ \mathbf Z ^ {n} $, | ||
| + | and is its own centralizer in $ \Gamma $. | ||
| + | The existence of a normal subgroup $ L $ | ||
| + | of an abstract group $ \Gamma $ | ||
| + | possessing these properties is a sufficient condition for $ \Gamma $ | ||
| + | to be isomorphic to a crystallographic group [[#References|[7]]]. | ||
| − | The group | + | The group $ G $ |
| + | of linear parts of a crystallographic group $ \Gamma $ | ||
| + | preserves the lattice $ L $; | ||
| + | in other words, relative to a basis of $ L $ | ||
| + | the transformations in $ G $ | ||
| + | are represented by matrices with integer entries. | ||
| − | In order to specify a crystallographic group | + | In order to specify a crystallographic group $ \Gamma $ |
| + | it is necessary to specify — in addition to $ G $ | ||
| + | and $ L $— | ||
| + | a vector $ a ( g) $ | ||
| + | for each $ g \in G $ | ||
| + | such that the transformation | ||
| − | + | $$ | |
| + | x \mapsto gx + a ( g),\ \ | ||
| + | x \in E ^ {n} , | ||
| + | $$ | ||
| − | belongs to | + | belongs to $ \Gamma $. |
| + | The vector $ a ( g) $ | ||
| + | is defined up to addition by a vector from $ L $. | ||
| + | The mapping | ||
| − | + | $$ | |
| + | \alpha : \ | ||
| + | g \mapsto a ( g) + L | ||
| + | $$ | ||
| − | is a one-dimensional cocycle on | + | is a one-dimensional cocycle on $ G $ |
| + | with values in $ V/L $, | ||
| + | where $ V $ | ||
| + | is the vector space associated with $ E ^ {n} $. | ||
| − | Any triple | + | Any triple $ \{ G, L, \alpha \} $, |
| + | where $ G \subset \mathop{\rm GL} ( V) $ | ||
| + | is a finite linear group, $ L $ | ||
| + | is a $ G $- | ||
| + | invariant lattice and $ \alpha $ | ||
| + | a one-dimensional cocycle on $ G $ | ||
| + | with values in $ V/L $, | ||
| + | corresponds as just described with some crystallographic group. Under this correspondence, two triples $ \{ G, L, \alpha _ {1} \} $ | ||
| + | and $ \{ G, L, \alpha _ {2} \} $, | ||
| + | where $ \alpha _ {1} $ | ||
| + | and $ \alpha _ {2} $ | ||
| + | are cohomologous cocycles, correspond to equivalent crystallographic groups. To the zero cohomology class corresponds the split (or symmorphic) crystallographic group, which, relative to a suitable choice of an origin, is the set of all transformations | ||
| − | + | $$ | |
| + | x \mapsto gx + a \ ( x \in E ^ {n} ), | ||
| + | $$ | ||
| − | where | + | where $ g \in G, a \in L $. |
| − | In matrix interpretation, the description of all | + | In matrix interpretation, the description of all $ n $- |
| + | dimensional crystallographic groups reduces to the description of all finite groups of square matrices of order $ n $ | ||
| + | with integer entries (up to conjugacy in the group $ \mathop{\rm GL} _ {n} ( \mathbf Z ) $) | ||
| + | and, for each such group $ G $, | ||
| + | to the computation of the cohomology group $ H ^ {1} ( G, \mathbf R ^ {n} / \mathbf Z ^ {n} ) $. | ||
| − | Two cohomology classes define equivalent crystallographic groups if and only if they are transformed into one another by the normalizer of | + | Two cohomology classes define equivalent crystallographic groups if and only if they are transformed into one another by the normalizer of $ G $ |
| + | in $ \mathop{\rm GL} _ {n} ( \mathbf Z ) $. | ||
| + | Bieberbach's theorem 2 and a result due to H. Zassenhaus [[#References|[7]]] imply that the natural homomorphism | ||
| − | + | $$ | |
| + | H ^ {1} ( G, \mathbf R ^ {n} / \mathbf Z ^ {n} ) \rightarrow \ | ||
| + | H ^ {2} ( G, \mathbf Z ^ {n} ) | ||
| + | $$ | ||
| − | is an isomorphism. This is readily deduced from the exact cohomology sequence of | + | is an isomorphism. This is readily deduced from the exact cohomology sequence of $ G $. |
| − | Two crystallographic groups belong to the same class (arithmetical class) if their groups of linear parts are conjugate in | + | Two crystallographic groups belong to the same class (arithmetical class) if their groups of linear parts are conjugate in $ \mathop{\rm GL} _ {n} ( \mathbf R ) $( |
| + | in $ \mathop{\rm GL} _ {n} ( \mathbf Z ) $). | ||
| + | For $ n = 3 $ | ||
| + | there are 32 classes and 73 arithmetical classes of crystallographic groups. | ||
| − | Among the finite groups of matrices with integer entries one can single out the lattice symmetry groups, i.e. the groups of all orthogonal transformations that preserve some fixed lattice in a vector space (and are presented relative to a basis of this lattice). In 1848, A. Bravais determined all possible | + | Among the finite groups of matrices with integer entries one can single out the lattice symmetry groups, i.e. the groups of all orthogonal transformations that preserve some fixed lattice in a vector space (and are presented relative to a basis of this lattice). In 1848, A. Bravais determined all possible $ 3 $- |
| + | dimensional lattice symmetry groups and accordingly divided all $ 3 $- | ||
| + | dimensional lattices into 14 types (known as Bravais types). The subgroups of $ \mathop{\rm GL} _ {n} ( \mathbf Z ) $ | ||
| + | that are lattice symmetry groups are called Bravais subgroups. | ||
| − | The Bravais subgroups may also be interpreted as stabilizer subgroups for the natural action of | + | The Bravais subgroups may also be interpreted as stabilizer subgroups for the natural action of $ \mathop{\rm GL} _ {n} ( \mathbf Z ) $ |
| + | on the set of positive-definite quadratic forms in $ n $ | ||
| + | variables. They may therefore be determined using reduction theory (see [[#References|[11]]] and [[Quadratic forms, reduction of|Quadratic forms, reduction of]]). Every maximal finite subgroup of $ \mathop{\rm GL} _ {n} ( \mathbf Z ) $ | ||
| + | is a Bravais subgroup (but the converse is not true). | ||
| − | The following table lists the number of finite subgroups in | + | The following table lists the number of finite subgroups in $ \mathop{\rm GL} _ {n} ( \mathbf Z ) $( |
| + | up to conjugacy).<table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ n $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1">Number of maximal finite subgroups</td> <td colname="3" style="background-color:white;" colspan="1">Number of Bravais subgroups</td> <td colname="4" style="background-color:white;" colspan="1">Number of finite subgroups</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">1</td> <td colname="2" style="background-color:white;" colspan="1">1</td> <td colname="3" style="background-color:white;" colspan="1">1</td> <td colname="4" style="background-color:white;" colspan="1">2</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">2</td> <td colname="2" style="background-color:white;" colspan="1">2</td> <td colname="3" style="background-color:white;" colspan="1">5</td> <td colname="4" style="background-color:white;" colspan="1">13</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">3</td> <td colname="2" style="background-color:white;" colspan="1">4</td> <td colname="3" style="background-color:white;" colspan="1">14</td> <td colname="4" style="background-color:white;" colspan="1">73</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">4</td> <td colname="2" style="background-color:white;" colspan="1">9</td> <td colname="3" style="background-color:white;" colspan="1">64</td> <td colname="4" style="background-color:white;" colspan="1">710</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">5</td> <td colname="2" style="background-color:white;" colspan="1">17</td> <td colname="3" style="background-color:white;" colspan="1">?</td> <td colname="4" style="background-color:white;" colspan="1">?</td> </tr> </tbody> </table> | ||
</td></tr> </table> | </td></tr> </table> | ||
| − | An intersection of Bravais subgroups is again a Bravais subgroup. The smallest Bravais subgroup | + | An intersection of Bravais subgroups is again a Bravais subgroup. The smallest Bravais subgroup $ \widehat{G} $ |
| + | containing the group $ G $ | ||
| + | of linear parts of a crystallographic group $ \Gamma $, | ||
| + | up to conjugacy in $ \mathop{\rm GL} _ {n} ( \mathbf R ) $( | ||
| + | in $ \mathop{\rm GL} _ {n} ( \mathbf Z ) $), | ||
| + | is known as the geometrical (arithmetical) holohedry of $ \Gamma $. | ||
| + | If $ \Gamma $ | ||
| + | is a crystallographic group in general position, in the sense that there is no affine transformation mapping it onto a crystallographic group whose lattice of parallel translations has lower symmetry, then $ \widehat{G} $ | ||
| + | is the lattice symmetry group of parallel translations of $ \Gamma $. | ||
| + | Two crystallographic groups belong to the same syngony (Bravais type) if their geometrical (arithmetical) holohedries coincide. For $ n = 3 $ | ||
| + | there are 7 syngonies and 14 Bravais types of crystallographic groups. | ||
==Linear representations of crystallographic groups.== | ==Linear representations of crystallographic groups.== | ||
| − | The irreducible finite-dimensional complex linear representations of a crystallographic group | + | The irreducible finite-dimensional complex linear representations of a crystallographic group $ \Gamma $ |
| + | are described as follows. Let $ \chi $ | ||
| + | be some character (a homomorphism into the multiplicative group of complex numbers) of the group $ L $, | ||
| + | put | ||
| − | + | $$ | |
| + | \Gamma _ \chi = \ | ||
| + | \{ {\gamma \in \Gamma } : { | ||
| + | \chi ( \gamma l \gamma ^ {-} 1) = | ||
| + | \chi ( l) \textrm{ for } \textrm{ all } l \in L } \} | ||
| + | $$ | ||
| − | and let | + | and let $ \sigma $ |
| + | be an irreducible representation of $ \Gamma _ \chi $ | ||
| + | such that $ \sigma ( l) = \chi ( l) \cdot 1 $, | ||
| + | where $ l \in L $. | ||
| + | Then the representation of $ \Gamma $ | ||
| + | induced by the representation $ \sigma $ | ||
| + | of its subgroup $ \Gamma _ \chi $( | ||
| + | see [[Induced representation|Induced representation]]) is irreducible. All irreducible representations of $ \Gamma $ | ||
| + | are obtained in this way (see [[#References|[9]]], [[#References|[10]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1a]</TD> <TD valign="top"> A. Bravais, "Abhandlung über die systeme von regelmässig auf seiner Ebene oder Raum vertheilten Punkten" , Teubner (1897)</TD></TR><TR><TD valign="top">[1b]</TD> <TD valign="top"> A. Bravais, "Abhandlung über symmetrische Polyeder" , Teubner (1890)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E.S. Fedorov, "The symmetry and structure of crystals. Fundamental works" , Moscow (1949) pp. 111–255 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A. Schoenflies, "Kristallsysteme und Kristallstruktur" , Teubner (1891)</TD></TR><TR><TD valign="top">[4a]</TD> <TD valign="top"> L. Bieberbach, "Ueber die Bewegungsgruppen der Euklidischen Räume I" ''Math. Ann.'' , '''70''' (1911) pp. 297–336</TD></TR><TR><TD valign="top">[4b]</TD> <TD valign="top"> L. Bieberbach, "Ueber die Bewegungsgruppen der Euklidischen Räume II" ''Math. Ann.'' , '''72''' (1912) pp. 400–412</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B. Delone, N. Padurov, A. Aleksandrov, "Mathematical foundation for the lattice analysis of crystals" , Moscow-Leningrad (1934) (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A.V. Shubnikov, "An atlas of crystallographic symmetry groups" , Moscow-Leningrad (1946) (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> H. Zassenhaus, "Ueber ein Algorithmus zur Bestimmung der Raumgruppen" ''Comm. Math. Helv.'' , '''21''' (1948) pp. 117–141</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A.I. Mal'tsev, "Classical algebra" , ''Selected works'' , '''1''' , Moscow (1976) pp. 371–375 (In Russian) {{MR|}} {{ZBL|0422.01024}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> G.Ya. Lyubarskii, "Anwendung der Gruppentheorie in der Physik" , Deutsch. Verlag Wissenschaft. (1962) (Translated from Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> D.K. Faddeev, "Tables of the fundamental unitary representations of Fedorov groups" , Moscow-Leningrad (1961) (In Russian) {{MR|158025}} {{ZBL|}} </TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> B.N. Delone, R.V. Galiulin, M.I. Shtrogrin, "On the Bravais types of lattices" ''J. Soviet Math.'' , '''4''' : 1 (1975) pp. 79–156 ''Itogi Nauki i Tekhn. Sovrem. Probl. Mat.'' , '''2''' (1973) pp. 119–254 {{MR|}} {{ZBL|0334.50005}} </TD></TR></table> | <table><TR><TD valign="top">[1a]</TD> <TD valign="top"> A. Bravais, "Abhandlung über die systeme von regelmässig auf seiner Ebene oder Raum vertheilten Punkten" , Teubner (1897)</TD></TR><TR><TD valign="top">[1b]</TD> <TD valign="top"> A. Bravais, "Abhandlung über symmetrische Polyeder" , Teubner (1890)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E.S. Fedorov, "The symmetry and structure of crystals. Fundamental works" , Moscow (1949) pp. 111–255 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A. Schoenflies, "Kristallsysteme und Kristallstruktur" , Teubner (1891)</TD></TR><TR><TD valign="top">[4a]</TD> <TD valign="top"> L. Bieberbach, "Ueber die Bewegungsgruppen der Euklidischen Räume I" ''Math. Ann.'' , '''70''' (1911) pp. 297–336</TD></TR><TR><TD valign="top">[4b]</TD> <TD valign="top"> L. Bieberbach, "Ueber die Bewegungsgruppen der Euklidischen Räume II" ''Math. Ann.'' , '''72''' (1912) pp. 400–412</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B. Delone, N. Padurov, A. Aleksandrov, "Mathematical foundation for the lattice analysis of crystals" , Moscow-Leningrad (1934) (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A.V. Shubnikov, "An atlas of crystallographic symmetry groups" , Moscow-Leningrad (1946) (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> H. Zassenhaus, "Ueber ein Algorithmus zur Bestimmung der Raumgruppen" ''Comm. Math. Helv.'' , '''21''' (1948) pp. 117–141</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A.I. Mal'tsev, "Classical algebra" , ''Selected works'' , '''1''' , Moscow (1976) pp. 371–375 (In Russian) {{MR|}} {{ZBL|0422.01024}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> G.Ya. Lyubarskii, "Anwendung der Gruppentheorie in der Physik" , Deutsch. Verlag Wissenschaft. (1962) (Translated from Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> D.K. Faddeev, "Tables of the fundamental unitary representations of Fedorov groups" , Moscow-Leningrad (1961) (In Russian) {{MR|158025}} {{ZBL|}} </TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> B.N. Delone, R.V. Galiulin, M.I. Shtrogrin, "On the Bravais types of lattices" ''J. Soviet Math.'' , '''4''' : 1 (1975) pp. 79–156 ''Itogi Nauki i Tekhn. Sovrem. Probl. Mat.'' , '''2''' (1973) pp. 119–254 {{MR|}} {{ZBL|0334.50005}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | Let | + | Let $ A $ |
| + | be the group of affine transformations of $ E ^ {n} $. | ||
| + | The translations in $ A $ | ||
| + | form a normal subgroup $ T $ | ||
| + | and the quotient $ A/T $ | ||
| + | is the group of linear transformations. Let $ G $ | ||
| + | be a subgroup of $ A $. | ||
| + | Then the translations in $ G $ | ||
| + | form a normal subgroup $ T \cap G $; | ||
| + | the quotient $ G/ ( T \cap G) \subset \mathop{\rm GL} ( E ^ {n} ) $ | ||
| + | is often called the point group of $ G $; | ||
| + | this is called the group of linear parts above. | ||
Fedorov obtained his classification results during 1885–1889, whereas Schoenflies obtained a classification around 1891. The correct list of 230 groups was found only after comparing the lists of Fedorov and Schoenflies (see [[#References|[a1]]] for historical and other remarks). The book [[#References|[a2]]] by L. Sohnke was known to both. | Fedorov obtained his classification results during 1885–1889, whereas Schoenflies obtained a classification around 1891. The correct list of 230 groups was found only after comparing the lists of Fedorov and Schoenflies (see [[#References|[a1]]] for historical and other remarks). The book [[#References|[a2]]] by L. Sohnke was known to both. | ||
| − | For maximal finite subgroups of | + | For maximal finite subgroups of $ \mathop{\rm GL} ( n, \mathbf Z ) $ |
| + | for $ n = 5, 6, 7 $ | ||
| + | one may consult [[#References|[a3]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.L.E. Schwartzenberger, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027190/c027190109.png" />-dimensional crystallography" , Pitman (1980)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L. Sohnke, "Entwicklung einer Theorie der Kristallstruktur" , Teubner (1879)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Plesken, M. Post, "On maximal finite irreducible subgroups of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027190/c027190110.png" /> I, II" ''Math. Computation'' , '''31''' (1977) pp. 536–551; 552–573</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Klemm, "Symmetrien von Ornamenten und Kristallen" , Springer (1982) {{MR|0663004}} {{ZBL|0482.20034}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J.J. Burkhardt, "Die Bewegungsgruppen der Kristallographie" , Birkhäuser (1947)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.L.E. Schwartzenberger, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027190/c027190109.png" />-dimensional crystallography" , Pitman (1980)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L. Sohnke, "Entwicklung einer Theorie der Kristallstruktur" , Teubner (1879)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Plesken, M. Post, "On maximal finite irreducible subgroups of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027190/c027190110.png" /> I, II" ''Math. Computation'' , '''31''' (1977) pp. 536–551; 552–573</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Klemm, "Symmetrien von Ornamenten und Kristallen" , Springer (1982) {{MR|0663004}} {{ZBL|0482.20034}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J.J. Burkhardt, "Die Bewegungsgruppen der Kristallographie" , Birkhäuser (1947)</TD></TR></table> | ||
Revision as of 17:31, 5 June 2020
A discrete group of motions of an $ n $-
dimensional Euclidean space $ E ^ {n} $
having a bounded fundamental domain. Two crystallographic groups are said to be equivalent if they are conjugate in the group of affine transformations of $ E ^ {n} $.
The origin of the theory of crystallographic groups is connected with the study of the symmetry of ornaments $ ( n = 2) $ and the structure of crystals $ ( n = 3) $. A classification of all planar (two-dimensional) and spatial (three-dimensional) crystallographic groups was achieved at the end of the 19th century by E.S. Fedorov and somewhat later by A. Schoenflies (see [2], [3], and also [6], [7], [9]). Up to equivalence, there are 17 planar and 219 spatial crystallographic groups; if, however, the spatial groups are considered up to conjugacy with respect to orientation-preserving affine transformations, their number is 230. In 1910, L. Bieberbach investigated crystallographic groups of arbitrary dimension . In particular, he proved the following theorems:
1) Any $ n $- dimensional crystallographic group $ \Gamma $ contains $ n $ linearly independent parallel translations; the group $ G $ of linear parts of the transformations from $ \Gamma $ is finite. (For $ n = 3 $ this was proved in [3].)
2) Two crystallographic groups are equivalent if and only if they are isomorphic as abstract groups.
3) For any $ n $, there are — up to equivalence — only finitely many $ n $- dimensional crystallographic groups (this is a solution to Hilbert's 18th problem).
Theorem 1 yields the following description of the structure of crystallographic groups as abstract groups. Let $ L $ be the set of all parallel translations in a crystallographic group $ \Gamma $. Then $ L $ is a normal subgroup of finite index, isomorphic to $ \mathbf Z ^ {n} $, and is its own centralizer in $ \Gamma $. The existence of a normal subgroup $ L $ of an abstract group $ \Gamma $ possessing these properties is a sufficient condition for $ \Gamma $ to be isomorphic to a crystallographic group [7].
The group $ G $ of linear parts of a crystallographic group $ \Gamma $ preserves the lattice $ L $; in other words, relative to a basis of $ L $ the transformations in $ G $ are represented by matrices with integer entries.
In order to specify a crystallographic group $ \Gamma $ it is necessary to specify — in addition to $ G $ and $ L $— a vector $ a ( g) $ for each $ g \in G $ such that the transformation
$$ x \mapsto gx + a ( g),\ \ x \in E ^ {n} , $$
belongs to $ \Gamma $. The vector $ a ( g) $ is defined up to addition by a vector from $ L $. The mapping
$$ \alpha : \ g \mapsto a ( g) + L $$
is a one-dimensional cocycle on $ G $ with values in $ V/L $, where $ V $ is the vector space associated with $ E ^ {n} $.
Any triple $ \{ G, L, \alpha \} $, where $ G \subset \mathop{\rm GL} ( V) $ is a finite linear group, $ L $ is a $ G $- invariant lattice and $ \alpha $ a one-dimensional cocycle on $ G $ with values in $ V/L $, corresponds as just described with some crystallographic group. Under this correspondence, two triples $ \{ G, L, \alpha _ {1} \} $ and $ \{ G, L, \alpha _ {2} \} $, where $ \alpha _ {1} $ and $ \alpha _ {2} $ are cohomologous cocycles, correspond to equivalent crystallographic groups. To the zero cohomology class corresponds the split (or symmorphic) crystallographic group, which, relative to a suitable choice of an origin, is the set of all transformations
$$ x \mapsto gx + a \ ( x \in E ^ {n} ), $$
where $ g \in G, a \in L $.
In matrix interpretation, the description of all $ n $- dimensional crystallographic groups reduces to the description of all finite groups of square matrices of order $ n $ with integer entries (up to conjugacy in the group $ \mathop{\rm GL} _ {n} ( \mathbf Z ) $) and, for each such group $ G $, to the computation of the cohomology group $ H ^ {1} ( G, \mathbf R ^ {n} / \mathbf Z ^ {n} ) $.
Two cohomology classes define equivalent crystallographic groups if and only if they are transformed into one another by the normalizer of $ G $ in $ \mathop{\rm GL} _ {n} ( \mathbf Z ) $. Bieberbach's theorem 2 and a result due to H. Zassenhaus [7] imply that the natural homomorphism
$$ H ^ {1} ( G, \mathbf R ^ {n} / \mathbf Z ^ {n} ) \rightarrow \ H ^ {2} ( G, \mathbf Z ^ {n} ) $$
is an isomorphism. This is readily deduced from the exact cohomology sequence of $ G $.
Two crystallographic groups belong to the same class (arithmetical class) if their groups of linear parts are conjugate in $ \mathop{\rm GL} _ {n} ( \mathbf R ) $( in $ \mathop{\rm GL} _ {n} ( \mathbf Z ) $). For $ n = 3 $ there are 32 classes and 73 arithmetical classes of crystallographic groups.
Among the finite groups of matrices with integer entries one can single out the lattice symmetry groups, i.e. the groups of all orthogonal transformations that preserve some fixed lattice in a vector space (and are presented relative to a basis of this lattice). In 1848, A. Bravais determined all possible $ 3 $- dimensional lattice symmetry groups and accordingly divided all $ 3 $- dimensional lattices into 14 types (known as Bravais types). The subgroups of $ \mathop{\rm GL} _ {n} ( \mathbf Z ) $ that are lattice symmetry groups are called Bravais subgroups.
The Bravais subgroups may also be interpreted as stabilizer subgroups for the natural action of $ \mathop{\rm GL} _ {n} ( \mathbf Z ) $ on the set of positive-definite quadratic forms in $ n $ variables. They may therefore be determined using reduction theory (see [11] and Quadratic forms, reduction of). Every maximal finite subgroup of $ \mathop{\rm GL} _ {n} ( \mathbf Z ) $ is a Bravais subgroup (but the converse is not true).
The following table lists the number of finite subgroups in $ \mathop{\rm GL} _ {n} ( \mathbf Z ) $(
up to conjugacy).
<tbody> </tbody>
|
An intersection of Bravais subgroups is again a Bravais subgroup. The smallest Bravais subgroup $ \widehat{G} $ containing the group $ G $ of linear parts of a crystallographic group $ \Gamma $, up to conjugacy in $ \mathop{\rm GL} _ {n} ( \mathbf R ) $( in $ \mathop{\rm GL} _ {n} ( \mathbf Z ) $), is known as the geometrical (arithmetical) holohedry of $ \Gamma $. If $ \Gamma $ is a crystallographic group in general position, in the sense that there is no affine transformation mapping it onto a crystallographic group whose lattice of parallel translations has lower symmetry, then $ \widehat{G} $ is the lattice symmetry group of parallel translations of $ \Gamma $. Two crystallographic groups belong to the same syngony (Bravais type) if their geometrical (arithmetical) holohedries coincide. For $ n = 3 $ there are 7 syngonies and 14 Bravais types of crystallographic groups.
Linear representations of crystallographic groups.
The irreducible finite-dimensional complex linear representations of a crystallographic group $ \Gamma $ are described as follows. Let $ \chi $ be some character (a homomorphism into the multiplicative group of complex numbers) of the group $ L $, put
$$ \Gamma _ \chi = \ \{ {\gamma \in \Gamma } : { \chi ( \gamma l \gamma ^ {-} 1) = \chi ( l) \textrm{ for } \textrm{ all } l \in L } \} $$
and let $ \sigma $ be an irreducible representation of $ \Gamma _ \chi $ such that $ \sigma ( l) = \chi ( l) \cdot 1 $, where $ l \in L $. Then the representation of $ \Gamma $ induced by the representation $ \sigma $ of its subgroup $ \Gamma _ \chi $( see Induced representation) is irreducible. All irreducible representations of $ \Gamma $ are obtained in this way (see [9], [10]).
References
| [1a] | A. Bravais, "Abhandlung über die systeme von regelmässig auf seiner Ebene oder Raum vertheilten Punkten" , Teubner (1897) |
| [1b] | A. Bravais, "Abhandlung über symmetrische Polyeder" , Teubner (1890) |
| [2] | E.S. Fedorov, "The symmetry and structure of crystals. Fundamental works" , Moscow (1949) pp. 111–255 (In Russian) |
| [3] | A. Schoenflies, "Kristallsysteme und Kristallstruktur" , Teubner (1891) |
| [4a] | L. Bieberbach, "Ueber die Bewegungsgruppen der Euklidischen Räume I" Math. Ann. , 70 (1911) pp. 297–336 |
| [4b] | L. Bieberbach, "Ueber die Bewegungsgruppen der Euklidischen Räume II" Math. Ann. , 72 (1912) pp. 400–412 |
| [5] | B. Delone, N. Padurov, A. Aleksandrov, "Mathematical foundation for the lattice analysis of crystals" , Moscow-Leningrad (1934) (In Russian) |
| [6] | A.V. Shubnikov, "An atlas of crystallographic symmetry groups" , Moscow-Leningrad (1946) (In Russian) |
| [7] | H. Zassenhaus, "Ueber ein Algorithmus zur Bestimmung der Raumgruppen" Comm. Math. Helv. , 21 (1948) pp. 117–141 |
| [8] | A.I. Mal'tsev, "Classical algebra" , Selected works , 1 , Moscow (1976) pp. 371–375 (In Russian) Zbl 0422.01024 |
| [9] | G.Ya. Lyubarskii, "Anwendung der Gruppentheorie in der Physik" , Deutsch. Verlag Wissenschaft. (1962) (Translated from Russian) |
| [10] | D.K. Faddeev, "Tables of the fundamental unitary representations of Fedorov groups" , Moscow-Leningrad (1961) (In Russian) MR158025 |
| [11] | B.N. Delone, R.V. Galiulin, M.I. Shtrogrin, "On the Bravais types of lattices" J. Soviet Math. , 4 : 1 (1975) pp. 79–156 Itogi Nauki i Tekhn. Sovrem. Probl. Mat. , 2 (1973) pp. 119–254 Zbl 0334.50005 |
Comments
Let $ A $ be the group of affine transformations of $ E ^ {n} $. The translations in $ A $ form a normal subgroup $ T $ and the quotient $ A/T $ is the group of linear transformations. Let $ G $ be a subgroup of $ A $. Then the translations in $ G $ form a normal subgroup $ T \cap G $; the quotient $ G/ ( T \cap G) \subset \mathop{\rm GL} ( E ^ {n} ) $ is often called the point group of $ G $; this is called the group of linear parts above.
Fedorov obtained his classification results during 1885–1889, whereas Schoenflies obtained a classification around 1891. The correct list of 230 groups was found only after comparing the lists of Fedorov and Schoenflies (see [a1] for historical and other remarks). The book [a2] by L. Sohnke was known to both.
For maximal finite subgroups of $ \mathop{\rm GL} ( n, \mathbf Z ) $ for $ n = 5, 6, 7 $ one may consult [a3].
References
| [a1] | R.L.E. Schwartzenberger, "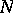 -dimensional crystallography" , Pitman (1980) -dimensional crystallography" , Pitman (1980) |
| [a2] | L. Sohnke, "Entwicklung einer Theorie der Kristallstruktur" , Teubner (1879) |
| [a3] | W. Plesken, M. Post, "On maximal finite irreducible subgroups of 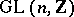 I, II" Math. Computation , 31 (1977) pp. 536–551; 552–573 I, II" Math. Computation , 31 (1977) pp. 536–551; 552–573 |
| [a4] | M. Klemm, "Symmetrien von Ornamenten und Kristallen" , Springer (1982) MR0663004 Zbl 0482.20034 |
| [a5] | J.J. Burkhardt, "Die Bewegungsgruppen der Kristallographie" , Birkhäuser (1947) |
Crystallographic group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Crystallographic_group&oldid=39414