Difference between revisions of "Bochner curvature tensor"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | b1106701.png | ||
| + | $#A+1 = 118 n = 7 | ||
| + | $#C+1 = 118 : ~/encyclopedia/old_files/data/B110/B.1100670 Bochner curvature tensor | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | In 1949, while studying the [[Betti number|Betti number]] of a [[Kähler manifold|Kähler manifold]], S. Bochner [[#References|[a1]]] (see also [[#References|[a26]]]), ad hoc and without giving any intrinsic geometric interpretation for its meaning or origin, introduced a new tensor as an analogue of the Weyl conformal curvature tensor in a [[Riemannian manifold|Riemannian manifold]]. In a complex local coordinate system in a $ 2n $- | |
| + | dimensional Kählerian manifold $ M ^ {2n } ( J _ \lambda ^ {k} ,g _ {\lambda \mu } ) $, | ||
| + | it is defined as follows: | ||
| − | + | $$ | |
| + | {\widetilde{B} } _ {jh ^ {*} lk ^ {*} } = R _ {jh ^ {*} lk ^ {*} } - | ||
| + | $$ | ||
| − | + | $$ | |
| + | - | ||
| + | { | ||
| + | \frac{1}{n + 2 } | ||
| + | } ( g _ {jk ^ {*} } R _ {h ^ {*} l } + g _ {lk ^ {*} } R _ {jh ^ {*} } + g _ {h ^ {*} l } R _ {jk ^ {*} } + g _ {jh ^ {*} } R _ {lk ^ {*} } ) + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | { | ||
| + | \frac{S}{2 ( n + 1 ) ( n + 2 ) } | ||
| + | } ( g _ {h ^ {*} l } g _ {jk ^ {*} } + g _ {jh ^ {*} } g _ {lk ^ {*} } ) , | ||
| + | $$ | ||
| − | + | where $ R _ {\lambda \mu \nu } ^ {k} $, | |
| + | $ R _ {\mu \nu } $ | ||
| + | and $ S $ | ||
| + | are the Riemannian curvature tensor (cf. [[Riemann tensor|Riemann tensor]]), the [[Ricci tensor|Ricci tensor]], and the [[Scalar curvature|scalar curvature]] tensor, respectively. This tensor is nowadays called the Bochner curvature tensor. | ||
| − | + | In 1967, S. Tachibana [[#References|[a16]]] gave a tensorial expression for $ {\widetilde{B} } $ | |
| + | in a real coordinate system in a complex $ m $- | ||
| + | dimensional ( $ m = 2n $) | ||
| + | Kähler manifold $ M ( J,g ) $, | ||
| + | as follows: | ||
| − | + | $$ | |
| + | B ( X,Y ) = R ( X,Y ) + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | { | ||
| + | \frac{1}{2 ( n + 2 ) } | ||
| + | } ( QY \wedge X - QX \wedge Y + QJY \wedge JX - | ||
| + | $$ | ||
| − | + | $$ | |
| + | - | ||
| + | {} QJX \wedge JY + 2g ( QJX,Y ) J + 2g ( JX,Y ) QJ ) - | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | - | ||
| + | { | ||
| + | \frac{S}{4 ( n + 1 ) ( n + 2 ) } | ||
| + | } ( Y \wedge X + JY \wedge JX + 2g ( JX,Y ) J ) , | ||
| + | $$ | ||
| + | |||
| + | $ X,Y,Z \in \mathfrak X ( M ) $( | ||
| + | here, $ \mathfrak X ( M ) $ | ||
| + | denotes the [[Lie algebra|Lie algebra]] of vector fields on $ M $), | ||
| + | where $ ( X \wedge Y ) Z = g ( Y,Z ) X - g ( X,Z ) Y $, | ||
| + | and $ R $, | ||
| + | $ Q $ | ||
| + | and $ S $ | ||
| + | are the Riemannian curvature tensor, the Ricci operator, and the scalar curvature on $ M $, | ||
| + | respectively. Bochner proved that $ B $ | ||
| + | has the components of $ {\widetilde{B} } $ | ||
| + | with respect to complex local coordinates. So, $ B $ | ||
| + | is also called the Bochner curvature tensor. Since then the tensors $ {\widetilde{B} } $ | ||
| + | and $ B $ | ||
| + | have been intensively studied on Kähler manifolds; see, e.g., [[#References|[a3]]], [[#References|[a16]]], [[#References|[a17]]], [[#References|[a22]]], [[#References|[a23]]], [[#References|[a24]]], [[#References|[a25]]], [[#References|[a26]]], [[#References|[a27]]], [[#References|[a28]]] (in particular, in [[#References|[a22]]] $ {\widetilde{B} } $ | ||
| + | is identified with the fourth-order Chern–Moser tensor [[#References|[a4]]] for CR-manifolds.) | ||
==Generalization.== | ==Generalization.== | ||
| − | M. Sitaramayya [[#References|[a15]]] and H. Mori [[#References|[a12]]] obtained a generalized Bochner curvature tensor | + | M. Sitaramayya [[#References|[a15]]] and H. Mori [[#References|[a12]]] obtained a generalized Bochner curvature tensor $ L _ {B} $ |
| + | as a component in its curvature tensor $ \mathbf L $ | ||
| + | by considering the decomposition theory of spaces of the generalized curvature tensor $ \mathbf L $ | ||
| + | on a real $ 2n $- | ||
| + | dimensional Kählerian vector space $ V $, | ||
| + | using the method of I.M. Singer and J.A. Thorpe [[#References|[a14]]] (see also [[#References|[a13]]]). If $ M $ | ||
| + | is a Kähler manifold and $ V = T _ {z} ( M ) $, | ||
| + | then $ L _ {B} = B $. | ||
| − | F. Tricerri and L. Vanhecke [[#References|[a21]]] generalized this notion, that is, they succeeded in defining the generalized Bochner curvature tensor | + | F. Tricerri and L. Vanhecke [[#References|[a21]]] generalized this notion, that is, they succeeded in defining the generalized Bochner curvature tensor $ B ( R ) $ |
| + | as a component of the element of spaces of arbitrary generalized curvature tensors $ R $ | ||
| + | on a real $ 2n $- | ||
| + | dimensional Hermitian vector space $ V $. | ||
| + | Of course, when $ M $ | ||
| + | is a Kähler manifold and $ V = T _ {z} ( M ) $, | ||
| + | $ B ( R ) = L _ {B} = B $. | ||
| + | Moreover, they also showed that, like the case of the Weyl tensor, $ B ( R ) $ | ||
| + | is invariant under conformal changes ( $ M ( g ) \rightarrow M ( {\widetilde{g} } ) $, | ||
| + | $ {\widetilde{g} } = e ^ \sigma g $, | ||
| + | where $ \sigma $ | ||
| + | is a $ C ^ \infty $- | ||
| + | function on $ M $) | ||
| + | in an arbitrary almost-Hermitian manifold $ M $. | ||
| + | In this context it means that they gave a geometrical interpretation of the Bochner curvature tensor. These results also show $ B ( R ) $ | ||
| + | to be a complete generalization of the Bochner curvature tensor on Kählerian manifolds to Hermitian manifolds (cf. also [[Hermitian structure|Hermitian structure]]). Some interesting applications for $ B ( R ) $ | ||
| + | have also been given. | ||
===Bochner curvature tensor on contact metric manifolds.=== | ===Bochner curvature tensor on contact metric manifolds.=== | ||
| − | In 1969, M. Matsumoto and G. Chūman [[#References|[a11]]] (see also [[#References|[a25]]]) defined on a | + | In 1969, M. Matsumoto and G. Chūman [[#References|[a11]]] (see also [[#References|[a25]]]) defined on a $ ( 2n + 1 ) $- |
| + | dimensional [[Sasakian manifold|Sasakian manifold]] $ M ( \phi, \xi, \eta,g ) $ | ||
| + | the contact Bochner curvature tensor, which is constructed from the Bochner curvature tensor in a Kählerian manifold by considering the Boothby–Wang fibering [[#References|[a2]]]. It is as follows: | ||
| − | + | $$ | |
| + | B ^ {c} ( X,Y ) = R ( X,Y ) + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | { | ||
| + | \frac{1}{2 ( n + 2 ) } | ||
| + | } ( QY \wedge X - QX \wedge Y + Q \phi Y \wedge \phi X - | ||
| + | $$ | ||
| − | + | $$ | |
| + | - | ||
| + | Q \phi X \wedge \phi Y + 2g ( Q \phi X,Y ) \phi + 2g ( \phi X,Y ) Q \phi + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | {} \eta ( Y ) QX \wedge \xi + \eta ( X ) \xi \wedge QY ) - | ||
| + | $$ | ||
| − | + | $$ | |
| + | - | ||
| + | { | ||
| + | \frac{k + 2n }{2 ( n + 2 ) } | ||
| + | } ( \phi Y \wedge \phi X + 2g ( \phi X,Y ) \phi ) - | ||
| + | $$ | ||
| − | + | $$ | |
| + | - | ||
| + | { | ||
| + | \frac{k - 4 }{2 ( n + 2 ) } | ||
| + | } Y \wedge X + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | { | ||
| + | \frac{k}{2 ( n + 2 ) } | ||
| + | } ( \eta ( Y ) \xi \wedge X + \eta ( X ) Y \wedge \xi ) , | ||
| + | $$ | ||
| − | where | + | where $ X,Y \in \mathfrak X ( M ) $, |
| + | $ k = { {( S + 2n ) } / {2 ( n + 1 ) } } $. | ||
| + | They called this tensor the $ C $- | ||
| + | Bochner tensor. Then they also proved that the $ C $- | ||
| + | Bochner tensor is invariant under $ D $- | ||
| + | homothetic deformations $ M ( \phi, \xi, \eta,g ) \rightarrow M ( \phi ^ {*} , \xi ^ {*} , \eta ^ {*} ,g ^ {*} ) $, | ||
| + | $ g ^ {*} = \alpha g + \alpha ( \alpha - 1 ) \eta \otimes \eta $, | ||
| + | $ \phi ^ {*} = \phi $, | ||
| + | $ \xi ^ {*} = \alpha ^ {- 1 } \xi $, | ||
| + | $ \eta ^ {*} = \alpha \eta $, | ||
| + | $ \alpha $ | ||
| + | a positive constant (see [[#References|[a19]]]), on a Sasakian manifold. After that many papers about $ B ^ {c} $ | ||
| + | on Sasakian manifolds were published; see, e.g., [[#References|[a5]]], [[#References|[a11]]], [[#References|[a25]]], [[#References|[a28]]]. | ||
| − | The tensor | + | The tensor $ B ^ {c} $ |
| + | is generally not invariant under $ D $- | ||
| + | homothetic deformations in more general manifolds, for example $ K $- | ||
| + | contact Riemannian manifolds and contact metric manifolds. So, a natural problem arises here: Is it possible to construct a "Bochner curvature tensor" for manifolds of more general classes than Sasakian manifolds? | ||
| − | In 1991, H. Endo [[#References|[a6]]] defined on a | + | In 1991, H. Endo [[#References|[a6]]] defined on a $ K $- |
| + | contact Riemannian manifold the $ E $- | ||
| + | contact Bochner curvature tensor, constructed from $ B ^ {c} $. | ||
| + | The $ E $- | ||
| + | contact Bochner curvature tensor is invariant under $ D $- | ||
| + | homothetic deformations on a $ K $- | ||
| + | contact Riemannian manifold and becomes $ B ^ {c} $ | ||
| + | on a Sasakian manifold. He also showed that a $ K $- | ||
| + | contact Riemannian manifold with vanishing $ E $- | ||
| + | contact Bochner curvature tensor is Sasakian. Moreover, in 1993 he constructed [[#References|[a7]]] on a manifold of more general class than $ K $- | ||
| + | contact Riemannian manifolds (to wit, a contact metric manifold), an extended contact Bochner curvature tensor by using a new tensor $ B ^ {es } $ | ||
| + | which modified $ B ^ {c} $. | ||
| + | It is called the $ EK $- | ||
| + | contact Bochner curvature tensor. Of course, the $ EK $- | ||
| + | contact Bochner curvature tensor coincides with $ B ^ {c} $ | ||
| + | on a Sasakian manifold and is invariant under $ D $- | ||
| + | homothetic deformations on a contact metric manifold. Furthermore, he proved that contact metric manifolds with vanishing $ EK $- | ||
| + | contact Bochner curvature tensor are Sasakian (see [[#References|[a8]]] for another study on $ B ^ {es } $). | ||
| − | ===Bochner curvature tensor on almost- | + | ===Bochner curvature tensor on almost- $ C ( \alpha ) $manifolds.=== |
| − | D. Janssens and L. Vanhecke [[#References|[a10]]] defined a Bochner curvature tensor on a class of almost-contact metric manifolds, i.e., almost- | + | D. Janssens and L. Vanhecke [[#References|[a10]]] defined a Bochner curvature tensor on a class of almost-contact metric manifolds, i.e., almost- $ C ( \alpha ) $ |
| + | manifolds, containing Sasakian manifolds, Kemmotsu manifolds, and co-symplectic manifolds (cf. [[#References|[a10]]]) with a decomposition theory of spaces of a class of the generalized curvature tensor on a real vector space. Some geometrical applications were also given. | ||
===Modified contact Bochner curvature tensor on almost co-symplectic manifolds.=== | ===Modified contact Bochner curvature tensor on almost co-symplectic manifolds.=== | ||
| − | Endo [[#References|[a9]]] considered a tensor which modifies | + | Endo [[#References|[a9]]] considered a tensor which modifies $ B ^ {c} $ |
| + | and introduced a new modified contact Bochner curvature tensor which is invariant with respect to $ D $- | ||
| + | homothetic deformations on an almost co-symplectic manifold $ M $. | ||
| + | He called it the $ AC $- | ||
| + | contact Bochner curvature tensor. If $ M $ | ||
| + | is a co-symplectic manifold, the $ AC $- | ||
| + | contact Bochner curvature turns into the main part of $ B ^ {c} $. | ||
| + | He also studied almost co-symplectic manifolds with vanishing $ AC $- | ||
| + | contact Bochner curvature tensor. | ||
| − | ===Bochner-type curvature tensor on the space defined by | + | ===Bochner-type curvature tensor on the space defined by $ \eta = 0 $.=== |
| − | In 1988, S. Tanno [[#References|[a20]]] defined on a contact metric manifold | + | In 1988, S. Tanno [[#References|[a20]]] defined on a contact metric manifold $ M $ |
| + | the Bochner-type curvature tensor ( $ B _ {zxy } ^ {u} $) | ||
| + | for the space defined by $ \eta = 0 $, | ||
| + | in such a way that its change under gauge transformations ( $ \eta \rightarrow {\widetilde \eta } = \sigma \eta $, | ||
| + | $ \sigma = { \mathop{\rm exp} } ( 2 \alpha ) $ | ||
| + | is a positive function on $ M $) | ||
| + | is natural; it has a generalized form of the Chern–Moser–Tanaka invariant [[#References|[a4]]], [[#References|[a18]]] ( $ ( B _ {zxy } ^ {u} ) $ | ||
| + | is not a tensor on $ M $). | ||
| + | From this he obtained a relation between $ ( B _ {zxy } ^ {u} ) $ | ||
| + | and the $ CR $- | ||
| + | structure corresponding to $ ( \eta, \phi ) $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Bochner, "Curvature and Betti numbers II" ''Ann. of Math.'' , '''50''' (1949) pp. 77–93</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W.M. Boothby, H.C. Wang, "On contact manifolds" ''Ann. of Math.'' , '''68''' (1958) pp. 721–734</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> B.Y. Chen, K. Yano, "Manifolds with vanishing Weyl or Bochner curvature tensor" ''J. Math. Soc. Japan'' , '''27''' (1975) pp. 106–112</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> S.S. Chern, J.K. Moser, "Real hypersurfaces in complex manifolds" ''Acta Math.'' , '''133''' (1974) pp. 219–271</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H. Endo, "On anti-invariant submanifolds in Sasakian manifolds with vanishing contact Bochner curvature tensor" ''Publ. Math. Debrecen'' , '''38''' (1991) pp. 263–271</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> H. Endo, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110670/b110670124.png" />-contact Riemannian manifolds with vanishing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110670/b110670125.png" />-contact Bochner curvature tensor" ''Colloq. Math.'' , '''62''' (1991) pp. 293–297</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> H. Endo, "On an extended contact Bochner curvature tensor on contact metric manifolds" ''Colloq. Math.'' , '''65''' (1993) pp. 33–41</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> H. Endo, "On certain tensor fields on contact metric manifolds. II" ''Publ. Math. Debrecen'' , '''44''' (1994) pp. 157–166</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> H. Endo, "On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110670/b110670126.png" />-contact Bochner curvature tensor field on almost cosymplectic manifolds" ''Publ. Inst. Math. (Beograd) (N.S.)'' , '''56''' (1994) pp. 102–110</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> D. Janssens, L. Vanhecke, "Almost contact structures and curvature tensors" ''Kodai Math. J.'' , '''4''' (1981) pp. 1–27</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> M. Matsumoto, G. Chūman, "On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110670/b110670127.png" />-Bochner curvature tensor" ''TRU. Math.'' , '''5''' (1967) pp. 21–30</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> H. Mori, "On the decomposition of generalized <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110670/b110670128.png" />-curvature tensor fields" ''Tôhoku Math. J.'' , '''25''' (1973) pp. 225–235</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> K. Nomizu, "On the decomposition of generalized curvature tensor fields" , ''Differential Geometry (In Honour of K. Yano)'' , Kinokuniya (1972) pp. 335–345</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> I.M. Singer, J.A. Thorpe, "The curvature of 4-dimensional Einstein spaces" , ''Global Analysis (In Honour of K. Kodaira)'' , Univ. Tokyo Press (1969) pp. 355–365</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> M. Sitaramayya, "Curvature tensors in Kähler manifolds" ''Trans. Amer. Math. Soc.'' , '''183''' (1973) pp. 341–353</TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> S. Tachibana, "On the Bochner curvature tensor" ''Natur. Sci. Rep. Ochanomizu Univ.'' , '''18''' (1967) pp. 15–19</TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> S. Tachibana, R.C. Liu, "Notes on Kaehlerian metrics with vanishing Bochner curvature tensor" ''Kōdai Math. Sem. Rep.'' , '''22''' (1970) pp. 313–321</TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> N. Tanaka, "On non-degenerate real hypersurfaces, graded Lie algebras and Cartan connections" ''Japan. J. Math. (N.S.)'' , '''2''' (1976) pp. 131–190</TD></TR><TR><TD valign="top">[a19]</TD> <TD valign="top"> S. Tanno, "Partially conformal transformations with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110670/b110670129.png" />-dimensional distributions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110670/b110670130.png" />-dimensional Riemannian manifolds" ''Tôhoku Math. J.'' , '''17''' (1965) pp. 358–409</TD></TR><TR><TD valign="top">[a20]</TD> <TD valign="top"> S. Tanno, "The Bochner type curvature tensor of contact Riemannian structure" ''Hokkaido Math. J.'' , '''19''' (1990) pp. 55–66</TD></TR><TR><TD valign="top">[a21]</TD> <TD valign="top"> F. Tricerri, L. Vanhecke, "Curvature tensors on almost Hermitian manifolds" ''Trans. Amer. Math. Soc.'' , '''267''' (1981) pp. 365–398</TD></TR><TR><TD valign="top">[a22]</TD> <TD valign="top"> S.M. Webster, "On the pseudo-conformal geometry of a Kaehler manifold" ''Math. Z.'' , '''157''' (1977) pp. 265–270</TD></TR><TR><TD valign="top">[a23]</TD> <TD valign="top"> K. Yano, "Manifolds and submanifolds with vanishing Weyl or Bochner curvature tensor" , ''Proc. Symp. Pure Math.'' , '''27''' , Amer. Math. Soc. (1975) pp. 253–262</TD></TR><TR><TD valign="top">[a24]</TD> <TD valign="top"> K. Yano, "Differential geometry of totally real submanifolds" , ''Topics in Differential Geometry'' , Acad. Press (1976) pp. 173–184</TD></TR><TR><TD valign="top">[a25]</TD> <TD valign="top"> K. Yano, "Anti-invariant submanifolds of a Sasakian manifold with vanishing contact Bochner curvature tensor" ''J. Diff. Geom.'' , '''12''' (1977) pp. 153–170</TD></TR><TR><TD valign="top">[a26]</TD> <TD valign="top"> K. Yano, S. Bochner, "Curvature and Betti numbers" , ''Annals of Math. Stud.'' , '''32''' , Princeton Univ. Press (1953)</TD></TR><TR><TD valign="top">[a27]</TD> <TD valign="top"> K. Yano, S. Ishihara, "Kaehlerian manifolds with constant scalar curvature whose Bochner curvature tensor vanishes" ''Hokkaido Math. J.'' , '''3''' (1974) pp. 297–304</TD></TR><TR><TD valign="top">[a28]</TD> <TD valign="top"> K. Yano, M. Kon, "Structures on manifolds" , World Sci. (1984)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Bochner, "Curvature and Betti numbers II" ''Ann. of Math.'' , '''50''' (1949) pp. 77–93</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W.M. Boothby, H.C. Wang, "On contact manifolds" ''Ann. of Math.'' , '''68''' (1958) pp. 721–734</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> B.Y. Chen, K. Yano, "Manifolds with vanishing Weyl or Bochner curvature tensor" ''J. Math. Soc. Japan'' , '''27''' (1975) pp. 106–112</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> S.S. Chern, J.K. Moser, "Real hypersurfaces in complex manifolds" ''Acta Math.'' , '''133''' (1974) pp. 219–271</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H. Endo, "On anti-invariant submanifolds in Sasakian manifolds with vanishing contact Bochner curvature tensor" ''Publ. Math. Debrecen'' , '''38''' (1991) pp. 263–271</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> H. Endo, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110670/b110670124.png" />-contact Riemannian manifolds with vanishing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110670/b110670125.png" />-contact Bochner curvature tensor" ''Colloq. Math.'' , '''62''' (1991) pp. 293–297</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> H. Endo, "On an extended contact Bochner curvature tensor on contact metric manifolds" ''Colloq. Math.'' , '''65''' (1993) pp. 33–41</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> H. Endo, "On certain tensor fields on contact metric manifolds. II" ''Publ. Math. Debrecen'' , '''44''' (1994) pp. 157–166</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> H. Endo, "On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110670/b110670126.png" />-contact Bochner curvature tensor field on almost cosymplectic manifolds" ''Publ. Inst. Math. (Beograd) (N.S.)'' , '''56''' (1994) pp. 102–110</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> D. Janssens, L. Vanhecke, "Almost contact structures and curvature tensors" ''Kodai Math. J.'' , '''4''' (1981) pp. 1–27</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> M. Matsumoto, G. Chūman, "On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110670/b110670127.png" />-Bochner curvature tensor" ''TRU. Math.'' , '''5''' (1967) pp. 21–30</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> H. Mori, "On the decomposition of generalized <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110670/b110670128.png" />-curvature tensor fields" ''Tôhoku Math. J.'' , '''25''' (1973) pp. 225–235</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> K. Nomizu, "On the decomposition of generalized curvature tensor fields" , ''Differential Geometry (In Honour of K. Yano)'' , Kinokuniya (1972) pp. 335–345</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> I.M. Singer, J.A. Thorpe, "The curvature of 4-dimensional Einstein spaces" , ''Global Analysis (In Honour of K. Kodaira)'' , Univ. Tokyo Press (1969) pp. 355–365</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> M. Sitaramayya, "Curvature tensors in Kähler manifolds" ''Trans. Amer. Math. Soc.'' , '''183''' (1973) pp. 341–353</TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> S. Tachibana, "On the Bochner curvature tensor" ''Natur. Sci. Rep. Ochanomizu Univ.'' , '''18''' (1967) pp. 15–19</TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> S. Tachibana, R.C. Liu, "Notes on Kaehlerian metrics with vanishing Bochner curvature tensor" ''Kōdai Math. Sem. Rep.'' , '''22''' (1970) pp. 313–321</TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> N. Tanaka, "On non-degenerate real hypersurfaces, graded Lie algebras and Cartan connections" ''Japan. J. Math. (N.S.)'' , '''2''' (1976) pp. 131–190</TD></TR><TR><TD valign="top">[a19]</TD> <TD valign="top"> S. Tanno, "Partially conformal transformations with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110670/b110670129.png" />-dimensional distributions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110670/b110670130.png" />-dimensional Riemannian manifolds" ''Tôhoku Math. J.'' , '''17''' (1965) pp. 358–409</TD></TR><TR><TD valign="top">[a20]</TD> <TD valign="top"> S. Tanno, "The Bochner type curvature tensor of contact Riemannian structure" ''Hokkaido Math. J.'' , '''19''' (1990) pp. 55–66</TD></TR><TR><TD valign="top">[a21]</TD> <TD valign="top"> F. Tricerri, L. Vanhecke, "Curvature tensors on almost Hermitian manifolds" ''Trans. Amer. Math. Soc.'' , '''267''' (1981) pp. 365–398</TD></TR><TR><TD valign="top">[a22]</TD> <TD valign="top"> S.M. Webster, "On the pseudo-conformal geometry of a Kaehler manifold" ''Math. Z.'' , '''157''' (1977) pp. 265–270</TD></TR><TR><TD valign="top">[a23]</TD> <TD valign="top"> K. Yano, "Manifolds and submanifolds with vanishing Weyl or Bochner curvature tensor" , ''Proc. Symp. Pure Math.'' , '''27''' , Amer. Math. Soc. (1975) pp. 253–262</TD></TR><TR><TD valign="top">[a24]</TD> <TD valign="top"> K. Yano, "Differential geometry of totally real submanifolds" , ''Topics in Differential Geometry'' , Acad. Press (1976) pp. 173–184</TD></TR><TR><TD valign="top">[a25]</TD> <TD valign="top"> K. Yano, "Anti-invariant submanifolds of a Sasakian manifold with vanishing contact Bochner curvature tensor" ''J. Diff. Geom.'' , '''12''' (1977) pp. 153–170</TD></TR><TR><TD valign="top">[a26]</TD> <TD valign="top"> K. Yano, S. Bochner, "Curvature and Betti numbers" , ''Annals of Math. Stud.'' , '''32''' , Princeton Univ. Press (1953)</TD></TR><TR><TD valign="top">[a27]</TD> <TD valign="top"> K. Yano, S. Ishihara, "Kaehlerian manifolds with constant scalar curvature whose Bochner curvature tensor vanishes" ''Hokkaido Math. J.'' , '''3''' (1974) pp. 297–304</TD></TR><TR><TD valign="top">[a28]</TD> <TD valign="top"> K. Yano, M. Kon, "Structures on manifolds" , World Sci. (1984)</TD></TR></table> | ||
Revision as of 10:59, 29 May 2020
In 1949, while studying the Betti number of a Kähler manifold, S. Bochner [a1] (see also [a26]), ad hoc and without giving any intrinsic geometric interpretation for its meaning or origin, introduced a new tensor as an analogue of the Weyl conformal curvature tensor in a Riemannian manifold. In a complex local coordinate system in a $ 2n $-
dimensional Kählerian manifold $ M ^ {2n } ( J _ \lambda ^ {k} ,g _ {\lambda \mu } ) $,
it is defined as follows:
$$ {\widetilde{B} } _ {jh ^ {*} lk ^ {*} } = R _ {jh ^ {*} lk ^ {*} } - $$
$$ - { \frac{1}{n + 2 } } ( g _ {jk ^ {*} } R _ {h ^ {*} l } + g _ {lk ^ {*} } R _ {jh ^ {*} } + g _ {h ^ {*} l } R _ {jk ^ {*} } + g _ {jh ^ {*} } R _ {lk ^ {*} } ) + $$
$$ + { \frac{S}{2 ( n + 1 ) ( n + 2 ) } } ( g _ {h ^ {*} l } g _ {jk ^ {*} } + g _ {jh ^ {*} } g _ {lk ^ {*} } ) , $$
where $ R _ {\lambda \mu \nu } ^ {k} $, $ R _ {\mu \nu } $ and $ S $ are the Riemannian curvature tensor (cf. Riemann tensor), the Ricci tensor, and the scalar curvature tensor, respectively. This tensor is nowadays called the Bochner curvature tensor.
In 1967, S. Tachibana [a16] gave a tensorial expression for $ {\widetilde{B} } $ in a real coordinate system in a complex $ m $- dimensional ( $ m = 2n $) Kähler manifold $ M ( J,g ) $, as follows:
$$ B ( X,Y ) = R ( X,Y ) + $$
$$ + { \frac{1}{2 ( n + 2 ) } } ( QY \wedge X - QX \wedge Y + QJY \wedge JX - $$
$$ - {} QJX \wedge JY + 2g ( QJX,Y ) J + 2g ( JX,Y ) QJ ) - $$
$$ - { \frac{S}{4 ( n + 1 ) ( n + 2 ) } } ( Y \wedge X + JY \wedge JX + 2g ( JX,Y ) J ) , $$
$ X,Y,Z \in \mathfrak X ( M ) $( here, $ \mathfrak X ( M ) $ denotes the Lie algebra of vector fields on $ M $), where $ ( X \wedge Y ) Z = g ( Y,Z ) X - g ( X,Z ) Y $, and $ R $, $ Q $ and $ S $ are the Riemannian curvature tensor, the Ricci operator, and the scalar curvature on $ M $, respectively. Bochner proved that $ B $ has the components of $ {\widetilde{B} } $ with respect to complex local coordinates. So, $ B $ is also called the Bochner curvature tensor. Since then the tensors $ {\widetilde{B} } $ and $ B $ have been intensively studied on Kähler manifolds; see, e.g., [a3], [a16], [a17], [a22], [a23], [a24], [a25], [a26], [a27], [a28] (in particular, in [a22] $ {\widetilde{B} } $ is identified with the fourth-order Chern–Moser tensor [a4] for CR-manifolds.)
Generalization.
M. Sitaramayya [a15] and H. Mori [a12] obtained a generalized Bochner curvature tensor $ L _ {B} $ as a component in its curvature tensor $ \mathbf L $ by considering the decomposition theory of spaces of the generalized curvature tensor $ \mathbf L $ on a real $ 2n $- dimensional Kählerian vector space $ V $, using the method of I.M. Singer and J.A. Thorpe [a14] (see also [a13]). If $ M $ is a Kähler manifold and $ V = T _ {z} ( M ) $, then $ L _ {B} = B $.
F. Tricerri and L. Vanhecke [a21] generalized this notion, that is, they succeeded in defining the generalized Bochner curvature tensor $ B ( R ) $ as a component of the element of spaces of arbitrary generalized curvature tensors $ R $ on a real $ 2n $- dimensional Hermitian vector space $ V $. Of course, when $ M $ is a Kähler manifold and $ V = T _ {z} ( M ) $, $ B ( R ) = L _ {B} = B $. Moreover, they also showed that, like the case of the Weyl tensor, $ B ( R ) $ is invariant under conformal changes ( $ M ( g ) \rightarrow M ( {\widetilde{g} } ) $, $ {\widetilde{g} } = e ^ \sigma g $, where $ \sigma $ is a $ C ^ \infty $- function on $ M $) in an arbitrary almost-Hermitian manifold $ M $. In this context it means that they gave a geometrical interpretation of the Bochner curvature tensor. These results also show $ B ( R ) $ to be a complete generalization of the Bochner curvature tensor on Kählerian manifolds to Hermitian manifolds (cf. also Hermitian structure). Some interesting applications for $ B ( R ) $ have also been given.
Bochner curvature tensor on contact metric manifolds.
In 1969, M. Matsumoto and G. Chūman [a11] (see also [a25]) defined on a $ ( 2n + 1 ) $- dimensional Sasakian manifold $ M ( \phi, \xi, \eta,g ) $ the contact Bochner curvature tensor, which is constructed from the Bochner curvature tensor in a Kählerian manifold by considering the Boothby–Wang fibering [a2]. It is as follows:
$$ B ^ {c} ( X,Y ) = R ( X,Y ) + $$
$$ + { \frac{1}{2 ( n + 2 ) } } ( QY \wedge X - QX \wedge Y + Q \phi Y \wedge \phi X - $$
$$ - Q \phi X \wedge \phi Y + 2g ( Q \phi X,Y ) \phi + 2g ( \phi X,Y ) Q \phi + $$
$$ + {} \eta ( Y ) QX \wedge \xi + \eta ( X ) \xi \wedge QY ) - $$
$$ - { \frac{k + 2n }{2 ( n + 2 ) } } ( \phi Y \wedge \phi X + 2g ( \phi X,Y ) \phi ) - $$
$$ - { \frac{k - 4 }{2 ( n + 2 ) } } Y \wedge X + $$
$$ + { \frac{k}{2 ( n + 2 ) } } ( \eta ( Y ) \xi \wedge X + \eta ( X ) Y \wedge \xi ) , $$
where $ X,Y \in \mathfrak X ( M ) $, $ k = { {( S + 2n ) } / {2 ( n + 1 ) } } $. They called this tensor the $ C $- Bochner tensor. Then they also proved that the $ C $- Bochner tensor is invariant under $ D $- homothetic deformations $ M ( \phi, \xi, \eta,g ) \rightarrow M ( \phi ^ {*} , \xi ^ {*} , \eta ^ {*} ,g ^ {*} ) $, $ g ^ {*} = \alpha g + \alpha ( \alpha - 1 ) \eta \otimes \eta $, $ \phi ^ {*} = \phi $, $ \xi ^ {*} = \alpha ^ {- 1 } \xi $, $ \eta ^ {*} = \alpha \eta $, $ \alpha $ a positive constant (see [a19]), on a Sasakian manifold. After that many papers about $ B ^ {c} $ on Sasakian manifolds were published; see, e.g., [a5], [a11], [a25], [a28].
The tensor $ B ^ {c} $ is generally not invariant under $ D $- homothetic deformations in more general manifolds, for example $ K $- contact Riemannian manifolds and contact metric manifolds. So, a natural problem arises here: Is it possible to construct a "Bochner curvature tensor" for manifolds of more general classes than Sasakian manifolds?
In 1991, H. Endo [a6] defined on a $ K $- contact Riemannian manifold the $ E $- contact Bochner curvature tensor, constructed from $ B ^ {c} $. The $ E $- contact Bochner curvature tensor is invariant under $ D $- homothetic deformations on a $ K $- contact Riemannian manifold and becomes $ B ^ {c} $ on a Sasakian manifold. He also showed that a $ K $- contact Riemannian manifold with vanishing $ E $- contact Bochner curvature tensor is Sasakian. Moreover, in 1993 he constructed [a7] on a manifold of more general class than $ K $- contact Riemannian manifolds (to wit, a contact metric manifold), an extended contact Bochner curvature tensor by using a new tensor $ B ^ {es } $ which modified $ B ^ {c} $. It is called the $ EK $- contact Bochner curvature tensor. Of course, the $ EK $- contact Bochner curvature tensor coincides with $ B ^ {c} $ on a Sasakian manifold and is invariant under $ D $- homothetic deformations on a contact metric manifold. Furthermore, he proved that contact metric manifolds with vanishing $ EK $- contact Bochner curvature tensor are Sasakian (see [a8] for another study on $ B ^ {es } $).
Bochner curvature tensor on almost- $ C ( \alpha ) $manifolds.
D. Janssens and L. Vanhecke [a10] defined a Bochner curvature tensor on a class of almost-contact metric manifolds, i.e., almost- $ C ( \alpha ) $ manifolds, containing Sasakian manifolds, Kemmotsu manifolds, and co-symplectic manifolds (cf. [a10]) with a decomposition theory of spaces of a class of the generalized curvature tensor on a real vector space. Some geometrical applications were also given.
Modified contact Bochner curvature tensor on almost co-symplectic manifolds.
Endo [a9] considered a tensor which modifies $ B ^ {c} $ and introduced a new modified contact Bochner curvature tensor which is invariant with respect to $ D $- homothetic deformations on an almost co-symplectic manifold $ M $. He called it the $ AC $- contact Bochner curvature tensor. If $ M $ is a co-symplectic manifold, the $ AC $- contact Bochner curvature turns into the main part of $ B ^ {c} $. He also studied almost co-symplectic manifolds with vanishing $ AC $- contact Bochner curvature tensor.
Bochner-type curvature tensor on the space defined by $ \eta = 0 $.
In 1988, S. Tanno [a20] defined on a contact metric manifold $ M $ the Bochner-type curvature tensor ( $ B _ {zxy } ^ {u} $) for the space defined by $ \eta = 0 $, in such a way that its change under gauge transformations ( $ \eta \rightarrow {\widetilde \eta } = \sigma \eta $, $ \sigma = { \mathop{\rm exp} } ( 2 \alpha ) $ is a positive function on $ M $) is natural; it has a generalized form of the Chern–Moser–Tanaka invariant [a4], [a18] ( $ ( B _ {zxy } ^ {u} ) $ is not a tensor on $ M $). From this he obtained a relation between $ ( B _ {zxy } ^ {u} ) $ and the $ CR $- structure corresponding to $ ( \eta, \phi ) $.
References
| [a1] | S. Bochner, "Curvature and Betti numbers II" Ann. of Math. , 50 (1949) pp. 77–93 |
| [a2] | W.M. Boothby, H.C. Wang, "On contact manifolds" Ann. of Math. , 68 (1958) pp. 721–734 |
| [a3] | B.Y. Chen, K. Yano, "Manifolds with vanishing Weyl or Bochner curvature tensor" J. Math. Soc. Japan , 27 (1975) pp. 106–112 |
| [a4] | S.S. Chern, J.K. Moser, "Real hypersurfaces in complex manifolds" Acta Math. , 133 (1974) pp. 219–271 |
| [a5] | H. Endo, "On anti-invariant submanifolds in Sasakian manifolds with vanishing contact Bochner curvature tensor" Publ. Math. Debrecen , 38 (1991) pp. 263–271 |
| [a6] | H. Endo, "On 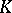 -contact Riemannian manifolds with vanishing -contact Riemannian manifolds with vanishing 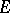 -contact Bochner curvature tensor" Colloq. Math. , 62 (1991) pp. 293–297 -contact Bochner curvature tensor" Colloq. Math. , 62 (1991) pp. 293–297 |
| [a7] | H. Endo, "On an extended contact Bochner curvature tensor on contact metric manifolds" Colloq. Math. , 65 (1993) pp. 33–41 |
| [a8] | H. Endo, "On certain tensor fields on contact metric manifolds. II" Publ. Math. Debrecen , 44 (1994) pp. 157–166 |
| [a9] | H. Endo, "On the 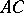 -contact Bochner curvature tensor field on almost cosymplectic manifolds" Publ. Inst. Math. (Beograd) (N.S.) , 56 (1994) pp. 102–110 -contact Bochner curvature tensor field on almost cosymplectic manifolds" Publ. Inst. Math. (Beograd) (N.S.) , 56 (1994) pp. 102–110 |
| [a10] | D. Janssens, L. Vanhecke, "Almost contact structures and curvature tensors" Kodai Math. J. , 4 (1981) pp. 1–27 |
| [a11] | M. Matsumoto, G. Chūman, "On the 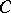 -Bochner curvature tensor" TRU. Math. , 5 (1967) pp. 21–30 -Bochner curvature tensor" TRU. Math. , 5 (1967) pp. 21–30 |
| [a12] | H. Mori, "On the decomposition of generalized 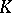 -curvature tensor fields" Tôhoku Math. J. , 25 (1973) pp. 225–235 -curvature tensor fields" Tôhoku Math. J. , 25 (1973) pp. 225–235 |
| [a13] | K. Nomizu, "On the decomposition of generalized curvature tensor fields" , Differential Geometry (In Honour of K. Yano) , Kinokuniya (1972) pp. 335–345 |
| [a14] | I.M. Singer, J.A. Thorpe, "The curvature of 4-dimensional Einstein spaces" , Global Analysis (In Honour of K. Kodaira) , Univ. Tokyo Press (1969) pp. 355–365 |
| [a15] | M. Sitaramayya, "Curvature tensors in Kähler manifolds" Trans. Amer. Math. Soc. , 183 (1973) pp. 341–353 |
| [a16] | S. Tachibana, "On the Bochner curvature tensor" Natur. Sci. Rep. Ochanomizu Univ. , 18 (1967) pp. 15–19 |
| [a17] | S. Tachibana, R.C. Liu, "Notes on Kaehlerian metrics with vanishing Bochner curvature tensor" Kōdai Math. Sem. Rep. , 22 (1970) pp. 313–321 |
| [a18] | N. Tanaka, "On non-degenerate real hypersurfaces, graded Lie algebras and Cartan connections" Japan. J. Math. (N.S.) , 2 (1976) pp. 131–190 |
| [a19] | S. Tanno, "Partially conformal transformations with respect to 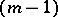 -dimensional distributions of -dimensional distributions of 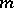 -dimensional Riemannian manifolds" Tôhoku Math. J. , 17 (1965) pp. 358–409 -dimensional Riemannian manifolds" Tôhoku Math. J. , 17 (1965) pp. 358–409 |
| [a20] | S. Tanno, "The Bochner type curvature tensor of contact Riemannian structure" Hokkaido Math. J. , 19 (1990) pp. 55–66 |
| [a21] | F. Tricerri, L. Vanhecke, "Curvature tensors on almost Hermitian manifolds" Trans. Amer. Math. Soc. , 267 (1981) pp. 365–398 |
| [a22] | S.M. Webster, "On the pseudo-conformal geometry of a Kaehler manifold" Math. Z. , 157 (1977) pp. 265–270 |
| [a23] | K. Yano, "Manifolds and submanifolds with vanishing Weyl or Bochner curvature tensor" , Proc. Symp. Pure Math. , 27 , Amer. Math. Soc. (1975) pp. 253–262 |
| [a24] | K. Yano, "Differential geometry of totally real submanifolds" , Topics in Differential Geometry , Acad. Press (1976) pp. 173–184 |
| [a25] | K. Yano, "Anti-invariant submanifolds of a Sasakian manifold with vanishing contact Bochner curvature tensor" J. Diff. Geom. , 12 (1977) pp. 153–170 |
| [a26] | K. Yano, S. Bochner, "Curvature and Betti numbers" , Annals of Math. Stud. , 32 , Princeton Univ. Press (1953) |
| [a27] | K. Yano, S. Ishihara, "Kaehlerian manifolds with constant scalar curvature whose Bochner curvature tensor vanishes" Hokkaido Math. J. , 3 (1974) pp. 297–304 |
| [a28] | K. Yano, M. Kon, "Structures on manifolds" , World Sci. (1984) |
Bochner curvature tensor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bochner_curvature_tensor&oldid=18427