Difference between revisions of "Birch-Tate conjecture"
Ulf Rehmann (talk | contribs) m (moved Birch–Tate conjecture to Birch-Tate conjecture: ascii title) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | b1105601.png | ||
| + | $#A+1 = 53 n = 8 | ||
| + | $#C+1 = 53 : ~/encyclopedia/old_files/data/B110/B.1100560 Birch\ANDTate conjecture | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Let $ {\mathcal O} _ {F} $ | |
| + | be the ring of integers of an algebraic number [[Field|field]] $ F $( | ||
| + | cf. also [[Algebraic number|Algebraic number]]). The Milnor $ K $- | ||
| + | group $ K _ {2} ( {\mathcal O} _ {F} ) $, | ||
| + | which is also called the tame kernel of $ F $, | ||
| + | is an [[Abelian group|Abelian group]] of finite order. | ||
| − | + | Let $ \zeta _ {F} $ | |
| + | denote the [[Dedekind zeta-function|Dedekind zeta-function]] of $ F $. | ||
| + | If $ F $ | ||
| + | is totally real, then $ \zeta _ {F} ( - 1 ) $ | ||
| + | is a non-zero rational number, and the Birch–Tate conjecture is about a relationship between $ \zeta _ {F} ( - 1 ) $ | ||
| + | and the order of $ K _ {2} ( {\mathcal O} _ {F} ) $. | ||
| − | + | Specifically, let $ w _ {2} ( F ) $ | |
| + | be the largest natural number $ N $ | ||
| + | such that the [[Galois group|Galois group]] of the cyclotomic extension over $ F $ | ||
| + | obtained by adjoining the $ N $ | ||
| + | th roots of unity to $ F $, | ||
| + | is an elementary Abelian $ 2 $- | ||
| + | group (cf. [[P-group| $ p $- | ||
| + | group]]). Then $ w _ {2} ( F ) \cdot \zeta _ {F} ( - 1 ) $ | ||
| + | is a rational integer, and the Birch–Tate conjecture states that if $ F $ | ||
| + | is a totally real number field, then | ||
| − | + | $$ | |
| + | \# K _ {2} ( {\mathcal O} _ {F} ) = \left | {w _ {2} ( F ) \cdot \zeta _ {F} ( - 1 ) } \right | . | ||
| + | $$ | ||
| − | + | A numerical example is as follows. For $ F = \mathbf Q $ | |
| + | one has $ w _ {2} ( \mathbf Q ) = 24 $, | ||
| + | $ \zeta _ {\mathbf Q} ( - 1 ) = - {1 / {12 } } $; | ||
| + | so it is predicted by the conjecture that the order of $ K _ {2} ( \mathbf Z ) $ | ||
| + | is $ 2 $, | ||
| + | which is correct. | ||
| − | + | What is known for totally real number fields $ F $? | |
| − | + | By work on the main conjecture of Iwasawa theory [[#References|[a6]]], the Birch–Tate conjecture was confirmed up to $ 2 $- | |
| + | torsion for Abelian extensions $ F $ | ||
| + | of $ \mathbf Q $. | ||
| − | + | Subsequently, [[#References|[a7]]], the Birch–Tate conjecture was confirmed up to $ 2 $- | |
| + | torsion for arbitrary totally real number fields $ F $. | ||
| − | + | Moreover, [[#References|[a7]]] (see the footnote on page 499) together with [[#References|[a4]]], also the $ 2 $- | |
| + | part of the Birch–Tate conjecture is confirmed for Abelian extensions $ F $ | ||
| + | of $ \mathbf Q $. | ||
| − | The Birch–Tate conjecture is related to the Lichtenbaum conjectures [[#References|[a5]]] for totally real number fields | + | By the above, all that is left to be considered is the $ 2 $- |
| + | part of the Birch–Tate conjecture for non-Abelian extensions $ F $ | ||
| + | of $ \mathbf Q $. | ||
| + | In this regard, for extensions $ F $ | ||
| + | of $ \mathbf Q $ | ||
| + | for which the $ 2 $- | ||
| + | primary subgroup of $ K _ {2} ( {\mathcal O} _ {F} ) $ | ||
| + | is elementary Abelian, the $ 2 $- | ||
| + | part of the Birch–Tate conjecture has been confirmed [[#References|[a3]]]. | ||
| + | |||
| + | In addition, explicit examples of families of non-Abelian extensions $ F $ | ||
| + | of $ \mathbf Q $ | ||
| + | for which the $ 2 $- | ||
| + | part of the Birch–Tate conjecture holds, have been given in [[#References|[a1]]], [[#References|[a2]]]. | ||
| + | |||
| + | The Birch–Tate conjecture is related to the Lichtenbaum conjectures [[#References|[a5]]] for totally real number fields $ F $. | ||
| + | For every odd natural number $ m $, | ||
| + | the Lichtenbaum conjectures express, up to $ 2 $- | ||
| + | torsion, the ratio of the orders of $ K _ {2m } ( {\mathcal O} _ {F} ) $ | ||
| + | and $ K _ {2m+1 } ( {\mathcal O} _ {F} ) $ | ||
| + | in terms of the value of the zeta-function $ \zeta _ {F} $ | ||
| + | at $ - m $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.E. Conner, J. Hurrelbrink, "Class number parity" , ''Pure Math.'' , '''8''' , World Sci. (1988)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Hurrelbrink, "Class numbers, units, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110560/b11056055.png" />" J.F. Jardine (ed.) V. Snaith (ed.) , ''Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110560/b11056056.png" />-theory: Connection with Geometry and Topology'' , ''NATO ASI Ser. C'' , '''279''' , Kluwer Acad. Publ. (1989) pp. 87–102</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Kolster, "The structure of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110560/b11056057.png" />-Sylow subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110560/b11056058.png" /> I" ''Comment. Math. Helv.'' , '''61''' (1986) pp. 376–388</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Kolster, "A relation between the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110560/b11056059.png" />-primary parts of the main conjecture and the Birch–Tate conjecture" ''Canad. Math. Bull.'' , '''32''' : 2 (1989) pp. 248–251</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> S. Lichtenbaum, "Values of zeta functions, étale cohomology, and algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110560/b11056060.png" />-theory" H. Bass (ed.) , ''Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110560/b11056061.png" />-theory II'' , ''Lecture Notes in Mathematics'' , '''342''' , Springer (1973) pp. 489–501</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> B. Mazur, A. Wiles, "Class fields of abelian extensions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110560/b11056062.png" />" ''Invent. Math.'' , '''76''' (1984) pp. 179–330</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> A. Wiles, "The Iwasawa conjecture for totally real fields" ''Ann. of Math.'' , '''131''' (1990) pp. 493–540</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.E. Conner, J. Hurrelbrink, "Class number parity" , ''Pure Math.'' , '''8''' , World Sci. (1988)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Hurrelbrink, "Class numbers, units, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110560/b11056055.png" />" J.F. Jardine (ed.) V. Snaith (ed.) , ''Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110560/b11056056.png" />-theory: Connection with Geometry and Topology'' , ''NATO ASI Ser. C'' , '''279''' , Kluwer Acad. Publ. (1989) pp. 87–102</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Kolster, "The structure of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110560/b11056057.png" />-Sylow subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110560/b11056058.png" /> I" ''Comment. Math. Helv.'' , '''61''' (1986) pp. 376–388</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Kolster, "A relation between the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110560/b11056059.png" />-primary parts of the main conjecture and the Birch–Tate conjecture" ''Canad. Math. Bull.'' , '''32''' : 2 (1989) pp. 248–251</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> S. Lichtenbaum, "Values of zeta functions, étale cohomology, and algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110560/b11056060.png" />-theory" H. Bass (ed.) , ''Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110560/b11056061.png" />-theory II'' , ''Lecture Notes in Mathematics'' , '''342''' , Springer (1973) pp. 489–501</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> B. Mazur, A. Wiles, "Class fields of abelian extensions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110560/b11056062.png" />" ''Invent. Math.'' , '''76''' (1984) pp. 179–330</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> A. Wiles, "The Iwasawa conjecture for totally real fields" ''Ann. of Math.'' , '''131''' (1990) pp. 493–540</TD></TR></table> | ||
Revision as of 10:59, 29 May 2020
Let $ {\mathcal O} _ {F} $
be the ring of integers of an algebraic number field $ F $(
cf. also Algebraic number). The Milnor $ K $-
group $ K _ {2} ( {\mathcal O} _ {F} ) $,
which is also called the tame kernel of $ F $,
is an Abelian group of finite order.
Let $ \zeta _ {F} $ denote the Dedekind zeta-function of $ F $. If $ F $ is totally real, then $ \zeta _ {F} ( - 1 ) $ is a non-zero rational number, and the Birch–Tate conjecture is about a relationship between $ \zeta _ {F} ( - 1 ) $ and the order of $ K _ {2} ( {\mathcal O} _ {F} ) $.
Specifically, let $ w _ {2} ( F ) $ be the largest natural number $ N $ such that the Galois group of the cyclotomic extension over $ F $ obtained by adjoining the $ N $ th roots of unity to $ F $, is an elementary Abelian $ 2 $- group (cf. $ p $- group). Then $ w _ {2} ( F ) \cdot \zeta _ {F} ( - 1 ) $ is a rational integer, and the Birch–Tate conjecture states that if $ F $ is a totally real number field, then
$$ \# K _ {2} ( {\mathcal O} _ {F} ) = \left | {w _ {2} ( F ) \cdot \zeta _ {F} ( - 1 ) } \right | . $$
A numerical example is as follows. For $ F = \mathbf Q $ one has $ w _ {2} ( \mathbf Q ) = 24 $, $ \zeta _ {\mathbf Q} ( - 1 ) = - {1 / {12 } } $; so it is predicted by the conjecture that the order of $ K _ {2} ( \mathbf Z ) $ is $ 2 $, which is correct.
What is known for totally real number fields $ F $?
By work on the main conjecture of Iwasawa theory [a6], the Birch–Tate conjecture was confirmed up to $ 2 $- torsion for Abelian extensions $ F $ of $ \mathbf Q $.
Subsequently, [a7], the Birch–Tate conjecture was confirmed up to $ 2 $- torsion for arbitrary totally real number fields $ F $.
Moreover, [a7] (see the footnote on page 499) together with [a4], also the $ 2 $- part of the Birch–Tate conjecture is confirmed for Abelian extensions $ F $ of $ \mathbf Q $.
By the above, all that is left to be considered is the $ 2 $- part of the Birch–Tate conjecture for non-Abelian extensions $ F $ of $ \mathbf Q $. In this regard, for extensions $ F $ of $ \mathbf Q $ for which the $ 2 $- primary subgroup of $ K _ {2} ( {\mathcal O} _ {F} ) $ is elementary Abelian, the $ 2 $- part of the Birch–Tate conjecture has been confirmed [a3].
In addition, explicit examples of families of non-Abelian extensions $ F $ of $ \mathbf Q $ for which the $ 2 $- part of the Birch–Tate conjecture holds, have been given in [a1], [a2].
The Birch–Tate conjecture is related to the Lichtenbaum conjectures [a5] for totally real number fields $ F $. For every odd natural number $ m $, the Lichtenbaum conjectures express, up to $ 2 $- torsion, the ratio of the orders of $ K _ {2m } ( {\mathcal O} _ {F} ) $ and $ K _ {2m+1 } ( {\mathcal O} _ {F} ) $ in terms of the value of the zeta-function $ \zeta _ {F} $ at $ - m $.
References
| [a1] | P.E. Conner, J. Hurrelbrink, "Class number parity" , Pure Math. , 8 , World Sci. (1988) |
| [a2] | J. Hurrelbrink, "Class numbers, units, and 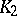 " J.F. Jardine (ed.) V. Snaith (ed.) , Algebraic " J.F. Jardine (ed.) V. Snaith (ed.) , Algebraic 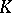 -theory: Connection with Geometry and Topology , NATO ASI Ser. C , 279 , Kluwer Acad. Publ. (1989) pp. 87–102 -theory: Connection with Geometry and Topology , NATO ASI Ser. C , 279 , Kluwer Acad. Publ. (1989) pp. 87–102 |
| [a3] | M. Kolster, "The structure of the  -Sylow subgroup of -Sylow subgroup of 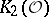 I" Comment. Math. Helv. , 61 (1986) pp. 376–388 I" Comment. Math. Helv. , 61 (1986) pp. 376–388 |
| [a4] | M. Kolster, "A relation between the  -primary parts of the main conjecture and the Birch–Tate conjecture" Canad. Math. Bull. , 32 : 2 (1989) pp. 248–251 -primary parts of the main conjecture and the Birch–Tate conjecture" Canad. Math. Bull. , 32 : 2 (1989) pp. 248–251 |
| [a5] | S. Lichtenbaum, "Values of zeta functions, étale cohomology, and algebraic 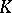 -theory" H. Bass (ed.) , Algebraic -theory" H. Bass (ed.) , Algebraic 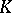 -theory II , Lecture Notes in Mathematics , 342 , Springer (1973) pp. 489–501 -theory II , Lecture Notes in Mathematics , 342 , Springer (1973) pp. 489–501 |
| [a6] | B. Mazur, A. Wiles, "Class fields of abelian extensions of 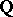 " Invent. Math. , 76 (1984) pp. 179–330 " Invent. Math. , 76 (1984) pp. 179–330 |
| [a7] | A. Wiles, "The Iwasawa conjecture for totally real fields" Ann. of Math. , 131 (1990) pp. 493–540 |
Birch-Tate conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Birch-Tate_conjecture&oldid=22123