Difference between revisions of "P-space"
(→-space in the sense of Morita.: cf Morita conjectures) |
(Add section: P-space in the sense of Arkhangel'skii. Points to feathered space.) |
||
| Line 4: | Line 4: | ||
Non-Archimedean ordered fields are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002012.png" />-spaces, in their order topology; thus, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002013.png" />-spaces occur in non-standard analysis. Another source of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002014.png" />-spaces is formed by the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002015.png" />-metrizable spaces of [[#References|[a5]]]. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002016.png" /> is a regular cardinal number (cf. also [[Cardinal number|Cardinal number]]), then an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002018.png" />-metrizable space is a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002019.png" /> with a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002020.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002021.png" /> to the ordinal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002022.png" /> that acts like a [[Metric|metric]]: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002023.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002024.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002025.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002026.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002027.png" /> is called an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002029.png" />-metric. A topology is formed, as for a [[Metric space|metric space]], using <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002030.png" />-balls: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002031.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002032.png" />. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002033.png" />-metrizable spaces are exactly the strongly zero-dimensional metric spaces [[#References|[a8]]] (cf. also [[Zero-dimensional space|Zero-dimensional space]]). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002034.png" /> is uncountable, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002035.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002036.png" />-space (and conversely). | Non-Archimedean ordered fields are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002012.png" />-spaces, in their order topology; thus, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002013.png" />-spaces occur in non-standard analysis. Another source of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002014.png" />-spaces is formed by the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002015.png" />-metrizable spaces of [[#References|[a5]]]. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002016.png" /> is a regular cardinal number (cf. also [[Cardinal number|Cardinal number]]), then an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002018.png" />-metrizable space is a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002019.png" /> with a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002020.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002021.png" /> to the ordinal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002022.png" /> that acts like a [[Metric|metric]]: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002023.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002024.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002025.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002026.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002027.png" /> is called an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002029.png" />-metric. A topology is formed, as for a [[Metric space|metric space]], using <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002030.png" />-balls: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002031.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002032.png" />. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002033.png" />-metrizable spaces are exactly the strongly zero-dimensional metric spaces [[#References|[a8]]] (cf. also [[Zero-dimensional space|Zero-dimensional space]]). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002034.png" /> is uncountable, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002035.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002036.png" />-space (and conversely). | ||
| − | One also employs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002037.png" />-spaces in the investigation of | + | One also employs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002037.png" />-spaces in the investigation of [[box product]]s [[#References|[a7]]]. If a product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002038.png" /> is endowed with the box topology, then the equivalence relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002039.png" /> defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002040.png" /> being finite defines a quotient space of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002041.png" />, denoted <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002042.png" />, that is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002043.png" />-space. The quotient mapping is open and the box product and its quotient share many properties. |
==<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002044.png" />-space in the sense of Morita.== | ==<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002044.png" />-space in the sense of Morita.== | ||
| Line 12: | Line 12: | ||
There is a characterization of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002062.png" />-spaces in terms of topological games [[#References|[a6]]]; let two players, I and II, play the following game on a topological space: player I chooses open sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002063.png" /> and player II chooses closed sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002064.png" />, with the proviso that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002065.png" />. Player II wins the play if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002066.png" />. One can show that Player II has a winning strategy if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002067.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002068.png" />-space. | There is a characterization of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002062.png" />-spaces in terms of topological games [[#References|[a6]]]; let two players, I and II, play the following game on a topological space: player I chooses open sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002063.png" /> and player II chooses closed sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002064.png" />, with the proviso that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002065.png" />. Player II wins the play if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002066.png" />. One can show that Player II has a winning strategy if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002067.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002068.png" />-space. | ||
| + | |||
| + | ==$P$-space in the sense of Arkhangel'skii.== | ||
| + | A completely-regular Hausdorff space having a [[feathering]] in some Hausdorff compactification: a [[feathered space]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K. Chiba, T.C. Przymusiński, M.E. Rudin, "Normality of products and Morita's conjectures" ''Topol. Appl.'' , '''22''' (1986) pp. 19–32</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L. Gillman, M. Henriksen, "Concerning rings of continuous functions" ''Trans. Amer. Math. Soc.'' , '''77''' (1954) pp. 340–362</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> K. Morita, "Products of normal spaces with metric spaces" ''Math. Ann.'' , '''154''' (1964) pp. 365–382</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> K. Morita, "Some problems on normality of products of spaces" J. Novák (ed.) , ''Proc. Fourth Prague Topological Symp. (Prague, August 1976)'' , Soc. Czech. Math. and Physicists , Prague (1977) pp. 296–297 (Part B: Contributed papers)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> R. Sikorski, "Remarks on some topological spaces of high power" ''Fundam. Math.'' , '''37''' (1950) pp. 125–136</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> R. Telgárski, "A characterization of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002069.png" />-spaces" ''Proc. Japan Acad.'' , '''51''' (1975) pp. 802–807</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> S.W. Williams, "Box products" K. Kunen (ed.) J.E. Vaughan (ed.) , ''Handbook of Set Theoretic Topology'' , North-Holland (1984) pp. Chap. 4; 169–200</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> J. de Groot, "Non-Archimedean metrics in topology" ''Proc. Amer. Math. Soc.'' , '''7''' (1956) pp. 948–953</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K. Chiba, T.C. Przymusiński, M.E. Rudin, "Normality of products and Morita's conjectures" ''Topol. Appl.'' , '''22''' (1986) pp. 19–32</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L. Gillman, M. Henriksen, "Concerning rings of continuous functions" ''Trans. Amer. Math. Soc.'' , '''77''' (1954) pp. 340–362</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> K. Morita, "Products of normal spaces with metric spaces" ''Math. Ann.'' , '''154''' (1964) pp. 365–382</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> K. Morita, "Some problems on normality of products of spaces" J. Novák (ed.) , ''Proc. Fourth Prague Topological Symp. (Prague, August 1976)'' , Soc. Czech. Math. and Physicists , Prague (1977) pp. 296–297 (Part B: Contributed papers)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> R. Sikorski, "Remarks on some topological spaces of high power" ''Fundam. Math.'' , '''37''' (1950) pp. 125–136</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> R. Telgárski, "A characterization of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002069.png" />-spaces" ''Proc. Japan Acad.'' , '''51''' (1975) pp. 802–807</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> S.W. Williams, "Box products" K. Kunen (ed.) J.E. Vaughan (ed.) , ''Handbook of Set Theoretic Topology'' , North-Holland (1984) pp. Chap. 4; 169–200</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> J. de Groot, "Non-Archimedean metrics in topology" ''Proc. Amer. Math. Soc.'' , '''7''' (1956) pp. 948–953</TD></TR></table> | ||
Revision as of 20:03, 23 September 2017
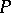 -space in the sense of Gillman–Henriksen.
-space in the sense of Gillman–Henriksen.
A 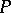 -space as defined in [a2] is a completely-regular space in which every point is a
-space as defined in [a2] is a completely-regular space in which every point is a  -point, i.e., every fixed prime ideal in the ring
-point, i.e., every fixed prime ideal in the ring  of real-valued continuous functions is maximal (cf. also Maximal ideal; Prime ideal); this is equivalent to saying that every
of real-valued continuous functions is maximal (cf. also Maximal ideal; Prime ideal); this is equivalent to saying that every  -subset is open (cf. also Set of type
-subset is open (cf. also Set of type  (
(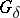 )). The latter condition is used to define
)). The latter condition is used to define  -spaces among general topological spaces. In [a5] these spaces were called
-spaces among general topological spaces. In [a5] these spaces were called 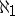 -additive, because countable unions of closed sets are closed.
-additive, because countable unions of closed sets are closed.
Non-Archimedean ordered fields are 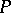 -spaces, in their order topology; thus,
-spaces, in their order topology; thus,  -spaces occur in non-standard analysis. Another source of
-spaces occur in non-standard analysis. Another source of 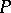 -spaces is formed by the
-spaces is formed by the 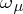 -metrizable spaces of [a5]. If
-metrizable spaces of [a5]. If  is a regular cardinal number (cf. also Cardinal number), then an
is a regular cardinal number (cf. also Cardinal number), then an  -metrizable space is a set
-metrizable space is a set  with a mapping
with a mapping 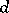 from
from 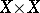 to the ordinal
to the ordinal  that acts like a metric:
that acts like a metric:  if and only if
if and only if 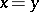 ;
; 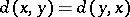 and
and  ;
; 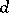 is called an
is called an 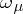 -metric. A topology is formed, as for a metric space, using
-metric. A topology is formed, as for a metric space, using  -balls:
-balls: 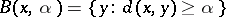 , where
, where  . The
. The  -metrizable spaces are exactly the strongly zero-dimensional metric spaces [a8] (cf. also Zero-dimensional space). If
-metrizable spaces are exactly the strongly zero-dimensional metric spaces [a8] (cf. also Zero-dimensional space). If  is uncountable, then
is uncountable, then 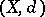 is a
is a 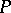 -space (and conversely).
-space (and conversely).
One also employs  -spaces in the investigation of box products [a7]. If a product
-spaces in the investigation of box products [a7]. If a product  is endowed with the box topology, then the equivalence relation
is endowed with the box topology, then the equivalence relation  defined by
defined by  being finite defines a quotient space of
being finite defines a quotient space of  , denoted
, denoted 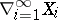 , that is a
, that is a 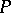 -space. The quotient mapping is open and the box product and its quotient share many properties.
-space. The quotient mapping is open and the box product and its quotient share many properties.
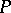 -space in the sense of Morita.
-space in the sense of Morita.
A 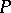 -space as defined in [a3] is a topological space
-space as defined in [a3] is a topological space  with the following covering property: Let
with the following covering property: Let  be a set and let
be a set and let 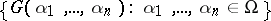 be a family of open sets (indexed by the set of finite sequences of elements of
be a family of open sets (indexed by the set of finite sequences of elements of  ). Then there is a family
). Then there is a family  of closed sets such that
of closed sets such that  and whenever a sequence
and whenever a sequence  satisfies
satisfies 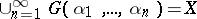 , then also
, then also 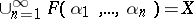 . K. Morita introduced
. K. Morita introduced 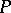 -spaces to characterize spaces whose products with all metrizable spaces are normal (cf. also Normal space): A space is a normal (paracompact)
-spaces to characterize spaces whose products with all metrizable spaces are normal (cf. also Normal space): A space is a normal (paracompact) 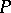 -space if and only if its product with every metrizable space is normal (paracompact, cf. also Paracompact space).
-space if and only if its product with every metrizable space is normal (paracompact, cf. also Paracompact space).
Morita [a4] conjectured that this characterization is symmetric in that a space is metrizable if and only if its product with every normal  -space is normal. K. Chiba, T.C. Przymusiński and M.E. Rudin [a1] showed that the conjecture is true if
-space is normal. K. Chiba, T.C. Przymusiński and M.E. Rudin [a1] showed that the conjecture is true if 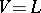 , i.e. Gödel's axiom of constructibility, holds (cf. also Gödel constructive set). These authors also showed that another conjecture of Morita is true without any extra set-theoretic axioms: If
, i.e. Gödel's axiom of constructibility, holds (cf. also Gödel constructive set). These authors also showed that another conjecture of Morita is true without any extra set-theoretic axioms: If 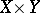 is normal for every normal space
is normal for every normal space 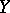 , then
, then 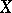 is discrete: cf. Morita conjectures.
is discrete: cf. Morita conjectures.
There is a characterization of 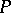 -spaces in terms of topological games [a6]; let two players, I and II, play the following game on a topological space: player I chooses open sets
-spaces in terms of topological games [a6]; let two players, I and II, play the following game on a topological space: player I chooses open sets 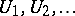 and player II chooses closed sets
and player II chooses closed sets 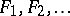 , with the proviso that
, with the proviso that 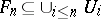 . Player II wins the play if
. Player II wins the play if  . One can show that Player II has a winning strategy if and only if
. One can show that Player II has a winning strategy if and only if  is a
is a 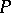 -space.
-space.
$P$-space in the sense of Arkhangel'skii.
A completely-regular Hausdorff space having a feathering in some Hausdorff compactification: a feathered space.
References
| [a1] | K. Chiba, T.C. Przymusiński, M.E. Rudin, "Normality of products and Morita's conjectures" Topol. Appl. , 22 (1986) pp. 19–32 |
| [a2] | L. Gillman, M. Henriksen, "Concerning rings of continuous functions" Trans. Amer. Math. Soc. , 77 (1954) pp. 340–362 |
| [a3] | K. Morita, "Products of normal spaces with metric spaces" Math. Ann. , 154 (1964) pp. 365–382 |
| [a4] | K. Morita, "Some problems on normality of products of spaces" J. Novák (ed.) , Proc. Fourth Prague Topological Symp. (Prague, August 1976) , Soc. Czech. Math. and Physicists , Prague (1977) pp. 296–297 (Part B: Contributed papers) |
| [a5] | R. Sikorski, "Remarks on some topological spaces of high power" Fundam. Math. , 37 (1950) pp. 125–136 |
| [a6] | R. Telgárski, "A characterization of  -spaces" Proc. Japan Acad. , 51 (1975) pp. 802–807 -spaces" Proc. Japan Acad. , 51 (1975) pp. 802–807 |
| [a7] | S.W. Williams, "Box products" K. Kunen (ed.) J.E. Vaughan (ed.) , Handbook of Set Theoretic Topology , North-Holland (1984) pp. Chap. 4; 169–200 |
| [a8] | J. de Groot, "Non-Archimedean metrics in topology" Proc. Amer. Math. Soc. , 7 (1956) pp. 948–953 |
P-space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=P-space&oldid=35013