Difference between revisions of "Wild knot"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| − | A knot | + | {{TEX|done}} |
| + | A knot $L$ in the Euclidean space $E^3$ (cf. [[Knot theory|Knot theory]]) such that there is no homeomorphism of $E^3$ onto itself under which $L$ would become a closed polygonal line consisting of a finite number of segments. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/w097980a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/w097980a.gif" /> | ||
| Line 5: | Line 6: | ||
Figure: w097980a | Figure: w097980a | ||
| − | Thus, knots containing the so-called Fox–Artin arcs — certain simple arcs obtained by a [[Wild imbedding|wild imbedding]] in | + | Thus, knots containing the so-called Fox–Artin arcs — certain simple arcs obtained by a [[Wild imbedding|wild imbedding]] in $E^3$ — are wild. For example, the fundamental group $\pi_1(E^3\setminus L)$ is non-trivial for the arc $L_1$ (Fig. a); this group is trivial for the arc $L_2$ (Fig. b), but $E^3\setminus L_2$ itself is not homeomorphic to the complement of a point in $E^3$. |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/w097980b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/w097980b.gif" /> | ||
Revision as of 08:57, 12 April 2014
A knot $L$ in the Euclidean space $E^3$ (cf. Knot theory) such that there is no homeomorphism of $E^3$ onto itself under which $L$ would become a closed polygonal line consisting of a finite number of segments.
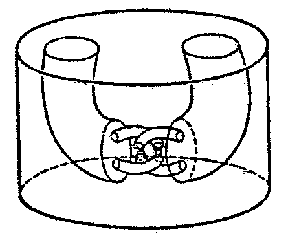
Figure: w097980a
Thus, knots containing the so-called Fox–Artin arcs — certain simple arcs obtained by a wild imbedding in $E^3$ — are wild. For example, the fundamental group $\pi_1(E^3\setminus L)$ is non-trivial for the arc $L_1$ (Fig. a); this group is trivial for the arc $L_2$ (Fig. b), but $E^3\setminus L_2$ itself is not homeomorphic to the complement of a point in $E^3$.
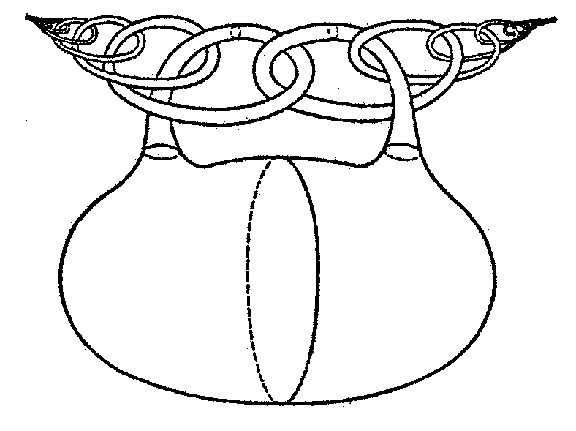
Figure: w097980b
For references see Wild sphere.
How to Cite This Entry:
Wild knot. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wild_knot&oldid=11381
Wild knot. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wild_knot&oldid=11381
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article