Difference between revisions of "Darboux theorem"
From Encyclopedia of Mathematics
(Importing text file) |
m |
||
| Line 1: | Line 1: | ||
| + | {{DEF}} | ||
| + | |||
| + | |||
If a real-valued function has a finite derivative at each point of an interval on the real axis, then, if the derivative assumes any two values on this interval, this derivative also assumes all the intermediate values on it. | If a real-valued function has a finite derivative at each point of an interval on the real axis, then, if the derivative assumes any two values on this interval, this derivative also assumes all the intermediate values on it. | ||
Revision as of 11:33, 28 April 2012
This page is deficient and requires revision. Please see Talk:Darboux theorem for further comments.
If a real-valued function has a finite derivative at each point of an interval on the real axis, then, if the derivative assumes any two values on this interval, this derivative also assumes all the intermediate values on it.
Comments
This is a kind of intermediate value theorem (for the derivative rather than the function). The following theorem holds for functions themselves: If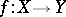 
is a continuous mapping between metric spaces, and if 
is a connected set, then 
is connected. (See, e.g., [a1].)
References
| [a1] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) |
How to Cite This Entry:
Darboux theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darboux_theorem&oldid=12655
Darboux theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darboux_theorem&oldid=12655
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article