Continuous mapping
A mapping 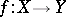 from a topological space
from a topological space  into a topological space
into a topological space  such that for every point
such that for every point 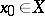 and for every neighbourhood
and for every neighbourhood 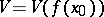 of its image
of its image  there is a neighbourhood
there is a neighbourhood 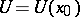 of
of  such the
such the 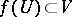 . This definition is a rephrasing of the neighbourhood definition of continuity of a function of a real variable (see Continuous function). There are many equivalent definitions of continuity. Thus, for the continuity of a mapping
. This definition is a rephrasing of the neighbourhood definition of continuity of a function of a real variable (see Continuous function). There are many equivalent definitions of continuity. Thus, for the continuity of a mapping 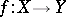 it is necessary and sufficient that any one of the following conditions holds:
it is necessary and sufficient that any one of the following conditions holds:
a) the inverse image 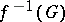 of every open set
of every open set 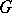 in
in 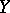 is open in
is open in 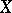 ;
;
b) the inverse image 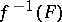 of every closed set
of every closed set 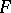 in
in 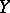 is closed in
is closed in 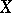 ;
;
c) 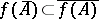 for every set
for every set 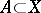 (the image of the closure is contained in the closure of the image).
(the image of the closure is contained in the closure of the image).
The concept of a continuous function, which was correctly stated already by B. Bolzano and A.L. Cauchy, played an important role in the mathematics of the 19th century. Weierstrass' function, which is nowhere differentiable, "Cantor's staircase" and Peano's curve pointed to the need of considering more special cases of continuity. The necessity of selecting special classes of mappings became even more urgent when continuous mappings of more general objects — topological spaces — were considered. One could mention the following important types of continuous mappings: topological mappings or homeomorphisms, perfect mappings, closed mappings, open mappings, and quotient mappings (cf. Homeomorphism; Closed mapping; Open mapping; Perfect mapping; Quotient mapping). If 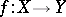 and
and 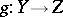 are two continuous mappings, then their composite
are two continuous mappings, then their composite 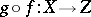 that is, the mapping
that is, the mapping 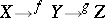 is also continuous. Every identity mapping
is also continuous. Every identity mapping 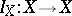 is evidently continuous. Therefore, topological spaces and continuous mappings form a category.
is evidently continuous. Therefore, topological spaces and continuous mappings form a category.
One of the aims of topology is the classification of both spaces and mappings. Its essence consists of the following: three fundamental and closely connected problems are selected. 1) In what case can every space of a certain fixed class  be mapped into some space of a class
be mapped into some space of a class  by a continuous mapping belonging to a class
by a continuous mapping belonging to a class  ? 2) By what intrinsic properties can one characterize spaces belonging to the class
? 2) By what intrinsic properties can one characterize spaces belonging to the class 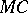 which contains the images of spaces in a class
which contains the images of spaces in a class  under continuous mappings in a class
under continuous mappings in a class 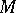 ? 3) Let
? 3) Let 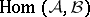 be the set of continuous mappings whose domains of definition are spaces in a class
be the set of continuous mappings whose domains of definition are spaces in a class 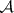 and whose ranges are spaces in a class
and whose ranges are spaces in a class  , and let
, and let 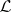 be some other class of mappings. What are the properties of mappings of the class
be some other class of mappings. What are the properties of mappings of the class 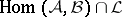 ?
?
These general statements comprise in particular, the following question: What topological properties are preserved by mappings of one kind or another under transition from a space to its image or inverse image? 1) Every  -dimensional space (in the sense of
-dimensional space (in the sense of 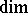 ) can be mapped essentially (see Essential mapping) onto an
) can be mapped essentially (see Essential mapping) onto an  -dimensional cube. 2) A pointwise-countable base is preserved under perfect (even under bifactorial) mappings. 3) Every closed mapping
-dimensional cube. 2) A pointwise-countable base is preserved under perfect (even under bifactorial) mappings. 3) Every closed mapping 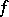 in the class
in the class 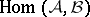 , where
, where 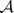 is the class of zero-dimensional spaces with a countable base and
is the class of zero-dimensional spaces with a countable base and 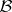 is the class of
is the class of  -dimensional spaces with a countable base, is at least
-dimensional spaces with a countable base, is at least 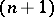 -fold.
-fold.
The first specific problems of this kind were solved at the beginning of the 20th century. Such are, for example, the representation of an arbitrary compactum as a continuous image of the Cantor perfect set (Aleksandrov's theorem); the characterization of metric spaces with a countable base as open continuous images of subspaces of the space of irrational numbers (Hausdorff's theorem); the description of locally connected continua as continuous images of an interval. The solution of these problem not only made it possible to answer questions about interrelationships between previously known spaces, but also led to the emergence of interesting new classes of spaces. Such are, for example, dyadic compacta, paracompact  -spaces, perfect
-spaces, perfect  -dimensional spaces, and pseudo-compact spaces.
-dimensional spaces, and pseudo-compact spaces.
The concept of a real-valued continuous function, that is, a continuous mapping of a topological space into 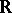 , which lies at the basis of the theory of functions, plays an important role also in general topology. Here one must mention first of all the Urysohn lemma, the Brouwer–Urysohn theorem on the extension of continuous functions from closed subsets of normal spaces, A.N. Tikhonov's definition of completely-regular spaces (cf. Completely-regular space), and the Stone–Weierstrass theorem. These and other investigations led to the creation of a theory of rings of continuous functions, the methods of which turned out to be quite fruitful in general topology.
, which lies at the basis of the theory of functions, plays an important role also in general topology. Here one must mention first of all the Urysohn lemma, the Brouwer–Urysohn theorem on the extension of continuous functions from closed subsets of normal spaces, A.N. Tikhonov's definition of completely-regular spaces (cf. Completely-regular space), and the Stone–Weierstrass theorem. These and other investigations led to the creation of a theory of rings of continuous functions, the methods of which turned out to be quite fruitful in general topology.
A substantial part of dimension theory is the study of the behaviour of dimensional characterizations of spaces under transition to an image or inverse image by mappings of one class or another. Here an important role is played by  -shifts,
-shifts,  -mappings,
-mappings, 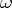 -mappings, essential mappings, finite-to-multiple mappings, countable-to-multiple mappings, zero-dimensional mappings,
-mappings, essential mappings, finite-to-multiple mappings, countable-to-multiple mappings, zero-dimensional mappings,  -dimensional mappings, etc. Here the method of continuous mappings leads to a mutual enrichment of and interrelations between domains of general topology of totally different origin, such as dimension theory, which has an intuitive geometric meaning, and the theory of cardinal invariants, which is abstract in character.
-dimensional mappings, etc. Here the method of continuous mappings leads to a mutual enrichment of and interrelations between domains of general topology of totally different origin, such as dimension theory, which has an intuitive geometric meaning, and the theory of cardinal invariants, which is abstract in character.
One of the characteristics of dimension is the possibility of extending a continuous mapping from a closed subset to an  -dimensional sphere. This is one of the versions of the theorem on the extension of mappings, which, like the fixed-point theorem closely connected with it, is of prime importance in branches of modern mathematics such as topology, algebra, function theory, functional analysis, and differential equations.
-dimensional sphere. This is one of the versions of the theorem on the extension of mappings, which, like the fixed-point theorem closely connected with it, is of prime importance in branches of modern mathematics such as topology, algebra, function theory, functional analysis, and differential equations.
One of the best studied classes of continuous mappings is that of the perfect irreducible mappings (cf. Perfect irreducible mapping). The theorem on the absolute of a regular space stimulated entire series of investigations in this domain. In particular, the concept of an absolute has been extended to the class of all Hausdorff spaces. Closely connected with the concept of a continuous mapping turned out to be that of a 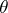 -proximity, which made it possible to given an intrinsic description of all perfect continuous inverse images of an arbitrary compactum. The extension of the theory of irreducible continuous mappings to the class of all Hausdorff spaces showed that continuous mappings are insufficient for the study of non-regular spaces and that is more natural to consider
-proximity, which made it possible to given an intrinsic description of all perfect continuous inverse images of an arbitrary compactum. The extension of the theory of irreducible continuous mappings to the class of all Hausdorff spaces showed that continuous mappings are insufficient for the study of non-regular spaces and that is more natural to consider 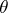 -continuous mappings in this case.
-continuous mappings in this case.
The selection of uniformly-continuous functions from the class of all numerical functions of one or several variables became one of the starting points of research leading to the notion of a uniform topology.
Continuous mappings of one type or another lie at the basis of the theory of retracts, splines and homology theory. A major role in modern mathematics is played by various aspects of the theory of multi-valued mappings (cf. Multi-valued mapping). Questions related to continuous mappings of Euclidean spaces are interesting by the wealth of ideas they contain.
References
| [1] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die allgemeine Topologie" , Deutsch. Verlag Wissenschaft. (1984) (Translated from Russian) |
| [2] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French) |
| [3] | J.L. Kelley, "General topology" , Springer (1975) |
| [4] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
| [5] | R.A. Aleksandryan, E.A. Mirzakhanyan, "General topology" , Moscow (1979) (In Russian) |
Comments
A mapping is called  -fold if every fibre of it has size at most
-fold if every fibre of it has size at most  (i.e. consists of at most
(i.e. consists of at most  points).
points).
The Brouwer–Urysohn theorem mentioned above is generally known as the Tietze–Urysohn theorem. H. Tietze proved it for metric spaces and P.S. Urysohn for normal spaces.
The statement that locally connected continua are continuous images of the unit interval is commonly known as the Hahn–Mazurkiewicz theorem.
More about rings of continuous functions can be found in [a1].
References
| [a1] | L. Gillman, M. Jerison, "Rings of continuous functions" , v. Nostrand-Reinhold (1960) |
Continuous mapping. V.V. Fedorchuk (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuous_mapping&oldid=16175