Watson transform
An integral transform $ g $
of a function $ f \in {L _ {2} } ( 0, \infty ) $,
defined as follows:
$$ \tag{1 } g( x) = \frac{d}{dx} \int\limits _ { 0 } ^ \infty \widetilde \omega ( xu) f( u) \frac{du}{u} . $$
Here $ x $ is a real variable, the kernel $ {\widetilde \omega } ( x) $ has the form
$$ \tag{2 } \widetilde \omega ( x) = \frac{x}{2 \pi } \mathop{\rm l}.i.m. _ {T \rightarrow \infty } \ \int\limits _ { -T}^ { T } \frac{\Omega \left ( \frac{1}{2} + it \right ) }{ \frac{1}{2} - it } x ^ {- ( t+ 1/2) } dt $$
(l.i.m. denotes the limit in the mean in $ L _ {2} $) and the function $ \Omega ( it + 1 / 2) $ satisfies the condition
$$ \Omega ( s) \Omega ( 1- s) = 1. $$
The following conditions are sufficient for the existence of the kernel $ {\widetilde \omega } ( x) $ and the inclusion $ {\widetilde \omega ( x) } / x \in {L _ {2} } ( 0, \infty ) $:
$$ \Omega \left ( \frac{1}{2} - it \right ) = \Omega \left ( \frac{1}{2} + it \right ) $$
and
$$ \frac{\Omega \left ( \frac{1}{2} + it \right ) }{ \frac{1}{2} - it } \in \ L _ {2} (- \infty , \infty ). $$
For a function $ f \in L _ {2} ( 0, \infty ) $, formula (1) defines the function $ g \in L _ {2} ( 0, \infty ) $ almost-everywhere. The inversion formula for the Watson transform (1) has the form
$$ f( x) = \frac{d}{dx} \int\limits _ { 0 } ^ \infty \widetilde \omega ( xu ) g( u) \frac{du}{u} . $$
Named after G.N. Watson [1], who was the first to study this transform.
References
| [1] | G.N. Watson, "General transforms" Proc. London Math. Soc. (2) , 35 (1933) pp. 156–199 |
Comments
Quite generally, let $ \psi $ be a Lebesgue-measure function in $ \mathbf R _ {>0} $ and let
$$ \phi = \int\limits _ { 0 } ^ { x } \psi ( x) dt . $$
The kernel $ \psi $( or $ \phi $) is called a generalized kernel, or kernel of a generalized transform, if
a) $ \psi ( x) $ is real valued on $ \mathbf R _ {>0} $;
b) $ x ^ {-1} \phi ( x) \in L _ {2} ( \mathbf R _ {>0 }) $;
c) $ \int _ {0} ^ \infty \phi ( xu ) \phi ( yu ) u ^ {-2} du = \min ( x, y) $.
The operator $ \Phi $ defined on $ L _ {2} ( \mathbf R _ {>0} ) $ by
$$ \Phi ( f )( x) = \frac{d}{dx} \int\limits _ { 0 } ^ \infty \frac{\phi ( xt) f( t) }{t} dt $$
is called a generalized transform or Watson transform.
References
| [a1] | G.O. Okikiolu, "Aspects of the theory of bounded operators in 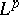 -spaces" , Acad. Press (1971) pp. §6.7 -spaces" , Acad. Press (1971) pp. §6.7 |
Watson transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Watson_transform&oldid=55217