Uniqueness properties of analytic functions
Properties of analytic functions that say that they are completely determined by their values on certain subsets of their domain of definition, or of its boundary; in this connection one may distinguish interior uniqueness properties and boundary uniqueness properties.
Interior uniqueness properties.
Let $ D $ be a domain in the complex plane $ \mathbf C = \mathbf C ^ {1} $. The classical interior uniqueness theorem for holomorphic (that is, single-valued analytic) functions on $ D $ states that if two holomorphic functions $ f ( z) $ and $ g ( z) $ in $ D $ coincide on some set $ E \subset D $ containing at least one limit point in $ D $, then $ f ( z) \equiv g ( z) $ everywhere in $ D $. In other words, if a holomorphic function $ f ( z) $ in $ D $ vanishes on a set $ E \subset D $ having at least one limit point in $ D $, then $ f ( z) \equiv 0 $. The proof of this interior uniqueness property of analytic functions shows that it is essentially a uniqueness property of power series in one complex variable $ z $. The uniqueness property remains valid for meromorphic functions $ f ( z) $ and $ g ( z) $ in $ D $ if one regards the poles of $ f ( z) $ and $ g ( z) $ as points at which the functions take the value $ \infty $.
In particular, if two analytic functions $ f ( z) $ and $ g ( z) $ coincide in an arbitrarily small neighbourhood of some point or on an arbitrarily small arc of some continuous curve, then $ f ( z) \equiv g ( z) $. Another corollary: The set of $ A $- points of an analytic function $ f ( z) $, that is, the set of points $ z $ at which $ f ( z) = A $, cannot have limit points inside the domain of definition $ D $, provided that $ f ( z) \not\equiv A $.
Two complete analytic functions in the sense of Weierstrass (cf. Complete analytic function) $ F ( z) $, $ G ( z) $ are, in general, multiple valued, and have the following interior uniqueness property: Let $ f ( z) $, $ g ( z) $ be single-valued elements, or branches, of $ F ( z) $ and $ G ( z) $, defined on domains $ D _ {1} $ and $ D _ {2} $, respectively, with $ D _ {1} \cap D _ {2} \neq \emptyset $. If $ f ( z) $ and $ g ( z) $ coincide on some set $ E \subset D _ {1} \cap D _ {2} $ having at least one limit point $ z _ {0} \in D _ {1} \cap D _ {2} $, then $ F ( z) $ and $ G ( z) $ have the same domain of existence and coincide everywhere as complete analytic functions.
These formulations of uniqueness properties do not carry over to the case of functions $ f ( z) $ of several complex variables $ z = ( z _ {1} \dots z _ {n} ) $, $ n > 1 $. For example, the analytic function $ f ( z) = z _ {1} z _ {2} $ is not identically zero, but vanishes on the analytic planes $ z _ {1} = 0 $ and $ z _ {2} = 0 $ of complex dimension $ n - 1 $. The following uniqueness properties hold for such functions:
1) If $ f ( z) $ is an analytic function on a domain $ D $ of the complex space $ \mathbf C ^ {n} $ and vanishes at all points of some non-empty open subset $ U \subset D $, then $ f ( z) \equiv 0 $ on $ D $.
2) If $ f ( z) $ is an analytic function on a domain $ D \subset \mathbf C ^ {n} $ that vanishes at some point $ z ^ {0} \in D $ together with all its partial derivatives $ \partial ^ {k} f / \partial z _ {1} ^ {k _ {1} } \dots \partial z _ {n} ^ {k _ {n} } $, $ k = k _ {1} + \dots + k _ {n} $; $ k _ {j} = 0 , 1 ,\dots $; $ j = 1 \dots n $, then $ f ( z) \equiv 0 $ on $ D $.
3) If $ f ( z) $ is an analytic function on a domain $ D \subset \mathbf C ^ {n} $ that vanishes in a real neighbourhood $ U _ \partial $ of a point $ z ^ {0} = x ^ {0} + iy ^ {0} \in D $, that is, on a set $ U _ \partial = \{ {z = x + iy \in \mathbf C ^ {n} } : {| x - x ^ {0} | < r, y = y ^ {0} } \} $, then $ f ( z) \equiv 0 $ on $ D $.
The difference between interior uniqueness properties in the cases $ n = 1 $ and $ n > 1 $ is caused by the different behaviour of power series in one and in several variables.
Boundary uniqueness properties.
The uniqueness theorem stated above for an analytic function $ f ( z) $ of a single complex variable admits several generalizations to the case when the zeros of $ f ( z) $ do not lie in the interior of the domain $ D $ of analyticity, but on its boundary $ \Gamma $. The most general and deepest boundary uniqueness theorems were obtained by N.N. Luzin and I.I. Privalov in 1925 (cf. also Luzin–Privalov theorems). Let $ D $ be a domain in the $ z $- plane bounded by a rectifiable curve $ \Gamma $, and let $ f ( z) $ be a meromorphic function in $ D $. Let $ \zeta _ {0} $ be a point of $ \Gamma $ at which the tangent to $ \Gamma $ exists; almost-all points of a rectifiable curve have this property. One says that $ f ( z) $ has an angular boundary value $ A $ at $ \zeta _ {0} $ if $ f ( z) $ tends to $ A $ as $ z $ tends to $ \zeta _ {0} $ remaining within the intersection of the domain $ D $ and the interior of any angle less than $ \pi $ with vertex $ \zeta _ {0} $ having the normal to $ \Gamma $ at $ \zeta _ {0} $ as its bisector.
The Luzin–Privalov boundary uniqueness theorem for angular boundary values then holds: If $ f ( z) $ is meromorphic in a domain $ D $ bounded by a rectifiable curve $ \Gamma $ and takes angular boundary values zero on a set $ E \subset \Gamma $ of positive Lebesgue measure, then $ f ( z) \equiv 0 $. In general, a meromorphic function need not have boundary values on $ \Gamma $. But for a fairly large class of meromorphic functions, for example, for functions of bounded characteristic, the existence of angular boundary values almost everywhere on $ \Gamma $ has been established.
Along with these, there are examples of bounded analytic functions in the unit disc $ D $ that converge to zero in all senses on a given set of points $ E $ of measure zero on the unit circle $ \Gamma $. Moreover, Luzin and Privalov have also constructed examples of analytic functions in the unit disc $ D $ having zero radial boundary values, that is, tending to zero along radii, everywhere on a set $ E \subset \Gamma $ of full measure $ 2 \pi $. It turns out that in uniqueness problems the concept of the Baire category of a set is also very important. In fact, there is a Luzin–Privalov boundary uniqueness theorem for radial boundary values: If the function $ f ( z) $ is meromorphic in the unit disc $ D $, has radial boundary values zero on a set $ E $ situated on an arc $ \sigma $ of the unit circle $ \Gamma $, and if $ E $ is metrically dense and of the second Baire category in $ \sigma $, then $ f ( z) \equiv 0 $. (A set $ E $ is called metrically dense in $ \sigma $ if the intersection of $ E $ with each subarc of $ \sigma $ has positive measure.)
See also Boundary properties of analytic functions; Limit set.
The investigation of boundary uniqueness properties of analytic functions of several complex variables has not yet achieved the same degree of completeness as for functions of a single variable (see [5], [6]).
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) pp. Chapt. 3 (Translated from Russian) |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) pp. Chapt. 2 (In Russian) |
| [3] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [4] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) |
| [5] | W. Rudin, "Function theory in the polydisc" , Benjamin (1969) |
| [6] | G.M. [G.M. Khenkin] Henkin, E.M. [E.M. Chirka] Čirka, "Boundary properties of holomorphic functions of several complex variables" J. Soviet Math. , 5 (1976) pp. 612–687 Itogi Nauk. Sovrem. Probl. Mat. , 4 (1975) pp. 13–142 |
| [7] | W. Rudin, "Function theory in the unit ball in 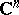 " , Springer (1980) " , Springer (1980) |
| [8] | P. Koosis, "Introduction to 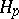 -spaces. With an appendix on Wolff's proof of the corona theorem" , Cambridge Univ. Press (1980) -spaces. With an appendix on Wolff's proof of the corona theorem" , Cambridge Univ. Press (1980) |
Comments
Analogues of the Luzin–Privalov examples of holomorphic functions, not identically equal to zero and with radial boundary values zero almost everywhere, have been found for the unit ball in $ \mathbf C ^ {n} $ too, see [a1].
References
| [a1] | M. Hakim, N. Sibony, "Boundary properties of holomorphic functions in the ball in 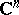 " Math. Ann. , 276 (1987) pp. 549–555 " Math. Ann. , 276 (1987) pp. 549–555 |
Uniqueness properties of analytic functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Uniqueness_properties_of_analytic_functions&oldid=49082