Unimodular element

unimodular vector

Let $ R $ be a ring with unit and $ M $ a right module over $ R $. An element $ x $ in $ M $ is called unimodular if $ \mathop{\rm ann} _ {R} ( x) = \{ {r \in R } : {xr = 0 } \} = 0 $ and the submodule $ \langle x \rangle $ generated by $ x $ has a complement $ N $ in $ M $, i.e. there is a submodule $ N \subset M $ such that $ \langle x \rangle \cap N = \{ 0 \} $, $ \langle x \rangle + N = M $, so that $ \langle x \rangle \oplus N = M $.

An element of a free module $ M $ that is part of a basis of $ M $ is unimodular. An element $ x \in M $ is unimodular if and only if there is a homomorphism of modules $ \rho : M \rightarrow R $ such that $ \rho ( x) = 1 $. A row (or column) of a unimodular matrix over $ R $ is unimodular. The question when the converse is true is important in algebraic $ K $- theory. Cf. also Stable rank.

References

[a1]	A.J. Hahn, O.T. O'Meara, "The classical groups and 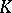-theory" , Springer (1989) pp. 9, §141ff MR1007302