Two-dimensional annulus
in topology
A topological image of the closed part of the plane comprised between two non-identical concentric circles. A two-dimensional annulus is an orientable two-dimensional manifold of genus zero with two boundary components.
Comments
Thus, a $ 2 $- dimensional annulus is homeomorphic to $ S ^ {1} \times I $, where $ S ^ {1} $ is the circle and $ I $ the interval. An $ n $- dimensional annulus is a space homeomorphic to $ S ^ {n-} 1 \times I $. The $ n $- dimensional annulus conjecture states that for any homeomorphism $ h: \mathbf R ^ {n} \rightarrow \mathbf R ^ {n} $ such that $ h( B ^ {n} ) \subset \mathop{\rm Int} ( B ^ {n} ) $, the interior of $ B ^ {n} $, the closed difference
$$ B ^ {n} \setminus h( \mathop{\rm Int} ( B ^ {n} )) $$
is homeomorphic to the annulus $ S ^ {n-} 1 \times I $. Here, $ B ^ {n} = \{ {x \in \mathbf R ^ {n} } : {\| x \| \leq 1 } \} $.
The stable homeomorphism conjecture asserts that any orientation-preserving homeomorphism $ h: \mathbf R ^ {n} \rightarrow \mathbf R ^ {n} $ can be written as a finite product, $ h = h _ {1} \dots h _ {m} $, where each $ h _ {i} $ is the identity on some open subset of $ \mathbf R ^ {n} $.
The stable homeomorphism conjecture for dimension $ n $ implies the annulus conjecture for dimension $ n $.
The stable homeomorphism conjecture (and hence the annulus conjecture) has finally been established for all $ n $: $ n= 1 $, classical; $ n= 2 $, [a6]; $ n= 3 $,
- $ n \geq 5 $,
[a3]; and, finally, $ n= 4 $, [a2], as an application of a special controlled $ h $- cobordism theorem in dimension $ 5 $, called the thin $ h $- cobordism theorem or Quinn's thin $ h $- cobordism theorem.
References
| [a1] | R.D. Edwards, "The solution of the 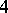 -dimensional annulus conjecture (after Frank Quinn)" Contemporary Math. , 35 (1984) pp. 211–264 -dimensional annulus conjecture (after Frank Quinn)" Contemporary Math. , 35 (1984) pp. 211–264 |
| [a2] | F. Quinn, "Ends of maps III: dimensions 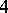 and and  " J. Diff. Geom. , 17 (1982) pp. 503–521 " J. Diff. Geom. , 17 (1982) pp. 503–521 |
| [a3] | R. Kirby, "Stable homeomorphisms and the annulus conjecture" Ann. of Math. , 89 (1969) pp. 575–582 |
| [a4a] | E.E. Moise, "Affine structures in  -manifolds I" Ann. of Math. , 54 (1951) pp. 506–533 -manifolds I" Ann. of Math. , 54 (1951) pp. 506–533 |
| [a4b] | E.E. Moise, "Affine structures in  -manifolds II, III" Ann. of Math. , 55 (1952) pp. 172–176; 203–222 -manifolds II, III" Ann. of Math. , 55 (1952) pp. 172–176; 203–222 |
| [a4c] | E.E. Moise, "Affine structures in  -manifolds IV" Ann. of Math. , 56 (1952) pp. 96–114 -manifolds IV" Ann. of Math. , 56 (1952) pp. 96–114 |
| [a5] | M. Brown, H. Gluck, "Stable structures on manifolds I-III" Ann. of Math. , 79 (1974) pp. 1–58 |
| [a6] | T. Radó, "Über den Begriff der Riemannsche Fläche" Acta Univ. Szeged , 2 (1924–1926) pp. 101–121 |
Two-dimensional annulus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Two-dimensional_annulus&oldid=49050