Transfinite diameter

of a compact set

A characteristic $ d = d ( E) $ of a compact set $ E $ in the complex plane serving as a geometric interpretation of the capacity of this set. Let $ E $ be a compact infinite set in the $ z $- plane. Then the quantity

$$ \tag{1 } d _ {n} ( E) = \ \left \{ \max _ {z _ {k} , z _ {l} \in E } \ \prod _ {1 \leq k < l \leq n } [ z _ {k} , z _ {l} ] \right \} ^ {2/[ n ( n - 1)] } , $$

$$ n = 2, 3 \dots $$

where $ [ a, b] = | a - b | $ is the Euclidean distance between $ a $ and $ b $, is called the $ n $- th diameter of $ E $. In particular, $ d _ {2} ( E) $ is the Euclidean diameter of $ E $. The points $ z _ {n,1} \dots z _ {n,n} $ of $ E $ for which the maximum on the right-hand side of (1) is realized are called the Fekete points (or Vandermonde nodes) for $ E $. The sequence of quantities $ d _ {n} ( E) $ is non-increasing: $ d _ {n + 1 } ( E) \leq d _ {n} ( E) $, $ n = 2, 3 \dots $ so that the following limit exists:

$$ \lim\limits _ {n \rightarrow \infty } d _ {n} ( E) = d ( E). $$

The quantity $ d ( E) $ is also called the transfinite diameter of $ E $. If $ E $ is a finite set, then one has $ d ( E) = 0 $. The transfinite diameter $ d ( E) $, the Chebyshev constant $ \tau ( E) $ and the capacity $ C ( E) $ are equal:

$$ d ( E) = \tau ( E) = C ( E). $$

The transfinite diameter of a set $ E $ has the following properties: 1) if $ E _ {1} \subset E $, then $ d ( E _ {1} ) \leq d ( E) $; 2) if $ a $ is a fixed complex number and $ E _ {1} = \{ {w } : {w = az, z \in E } \} $, then $ d ( E _ {1} ) = | a | d ( E) $; 3) if $ E _ \epsilon $ is the set of points at a distance at most $ \epsilon $ from $ E $, then $ \lim\limits _ {\epsilon \rightarrow 0 } d ( E _ \epsilon ) = d ( E) $; 4) if $ E ^ {*} $ is the set of roots of the equation

$$ Q ( z) = z ^ {k} + a _ {1} z ^ {k - 1 } + \dots + a _ {k} = w, $$

where $ Q ( z) $ is a given polynomial and $ w $ runs through $ E $, then $ d ( E ^ {*} ) = \{ d ( E) \} ^ {1/k} $. The transfinite diameter of a circle is equal to its radius; the transfinite diameter of a line segment is equal to a quarter of its length.

Let $ E $ be a bounded continuum and let $ D $ be the component of the complement of $ E $ with respect to the extended plane that contains the point $ \infty $. Then the transfinite diameter of $ E $ is equal to the conformal radius of $ D $( with respect to $ \infty $; cf. Conformal radius of a domain).

The corresponding notions for sets in the hyperbolic and elliptic planes are defined as follows. Consider as a model of the hyperbolic plane the disc $ | z | < 1 $ with metric defined by the line element $ ds _ {h} = | dz |/( 1 - | z | ^ {2} ) $ and suppose that $ E $ is a closed infinite set in $ | z | < 1 $. Then the $ n $- th hyperbolic diameter $ d _ {n,h} ( E) $ of $ E $ is defined by (1) in which

$$ \tag{2 } [ a, b] = \ \left | \frac{a - b }{1 - \overline{a}\; b } \ \right | $$

is the hyperbolic pseudo-distance between $ a $ and $ b $, that is, $ [ a, b] = \mathop{\rm tanh} \rho _ {h} ( a, b) $, where $ \rho _ {h} ( a, b) $ is the hyperbolic distance between $ a $ and $ b $ in $ | z | < 1 $( see Hyperbolic metric). As in the Euclidean case, the sequence $ d _ {n,h} ( E) $ is non-increasing and the following limit exists:

$$ \lim\limits _ {n \rightarrow \infty } d _ {n,h} ( E) = d _ {h} ( E). $$

It is called the hyperbolic transfinite diameter of $ E $. Define the hyperbolic Chebyshev constant $ \tau _ {h} ( E) $ and the hyperbolic capacity $ C _ {h} ( E) $ of $ E $ via the hyperbolic pseudo-distance (2) between the points of $ | z | < 1 $ by analogy with the Chebyshev constant $ \tau ( E) $ and capacity $ C ( E) $ defined via the Euclidean distance between points of the $ z $- plane. Then one obtains

$$ d _ {h} ( E) = \tau _ {h} ( E) = C _ {h} ( E). $$

The hyperbolic transfinite diameter is invariant under the full group of hyperbolic isometries. If $ E $ is a continuum, then there is a simple relationship between the hyperbolic transfinite diameter $ d _ {n} ( E) $ and conformal mapping. Namely, let $ E $ be a continuum in the disc $ | z | < 1 $ such that the complement of $ E $ with respect to this disc is conformally equivalent to the annulus $ r < | w | < 1 $, $ 0 < r < 1 $. Then $ r = d _ {n} ( E) $.

Consider as a model of the elliptic plane the extended complex $ z $- plane with the metric of its Riemann sphere $ K $ of diameter 1, tangent to the $ z $- plane at the point $ z = 0 $, that is, the metric defined by the line element

$$ ds _ {e} = \ \frac{| dz | }{1 + | z | ^ {2} } ; $$

furthermore, let the points $ z $ and $ z ^ {*} = - 1/z $ be identified; these correspond to diametrically-opposite points of $ K $ under stereographic projection of the extended $ z $- plane onto $ K $. Let $ E $ be a closed infinite set in the extended $ z $- plane, $ E \cap E ^ {*} = \emptyset $, where $ E ^ {*} = \{ {- 1/z } : {z \in E } \} $. Then the $ n $- th elliptic diameter $ d _ {n,e} ( E) $ of $ E $ is defined by (1), in which

$$ \tag{3 } [ a, b] = \ \left | \frac{a - b }{1 + \overline{a}\; b } \ \right | $$

is the elliptic pseudo-distance between points $ a $ and $ b $ of $ E $, that is, $ [ a, b] = \mathop{\rm tan} \rho _ {e} ( a, b) $, where $ \rho _ {e} ( a, b) $( $ < \pi /2 $) is the elliptic distance between $ a $ and $ b $. As in the previous cases, the sequence $ d _ {n,e} ( E) $ is non-increasing and the following limit, called the elliptic transfinite diameter of $ E $, exists:

$$ \lim\limits _ {n \rightarrow \infty } d _ {n,e} ( E) = d _ {e} ( E). $$

Define the elliptic Chebyshev constant $ \tau _ {e} ( E) $ and the elliptic capacity $ C _ {e} ( E) $ of $ E $ via the elliptic pseudo-distance (3). Then one obtains:

$$ d _ {e} ( E) = \tau _ {e} ( E) = C _ {e} ( E). $$

The elliptic transfinite diameter $ d _ {e} ( E) $ is invariant under the group of fractional-linear transformations

$$ z \rightarrow \ \frac{pz + q }{- \overline{q}\; z + p } ,\ \ | p | ^ {2} + | q | ^ {2} = 1, $$

of the extended $ z $- plane onto itself, supplemented by the group of reflections in the elliptic lines. The first of these groups is isomorphic to the group of reflections of $ K $ about planes passing through its centre. With this definition the elliptic transfinite diameter of $ E $ is related to conformal mapping in the following way. If $ E $ is a continuum in the extended $ z $- plane, $ E \cap E ^ {*} = \emptyset $, and the complement of $ E \cup E ^ {*} $ with respect to the extended plane is conformally equivalent to the annulus $ r < | w | < 1/r $, $ 0 < r < 1 $, then $ r = d _ {e} ( E) $.

The notion of the transfinite diameter can be generalized to compacta $ E $ in a multi-dimensional Euclidean space $ \mathbf R ^ {m} $, $ m \geq 2 $, and is connected with potential theory. Let, for points $ x \in \mathbf R ^ {m} $,

$$ H (| x |) = \ \left \{ \begin{array}{ll} \mathop{\rm ln} { \frac{1}{| x | } } & \textrm{ for } m = 2, \\ { \frac{1}{| x | ^ {m - 2 } } } & \textrm{ for } m \geq 3, \\ \end{array} \right .$$

be a fundamental solution of the Laplace equation, and for the set of points $ ( x _ {j} ) _ {j = 1 } ^ {n} \subset E $, let

$$ \chi _ {n} ( E) = \ \inf \left \{ { { \frac{2}{n ( n - 1) } } \sum _ {\begin{array}{c} j, k = 1 \\ j < k \end{array} } ^ { n } H (| x _ {j} - x _ {k} |) } : { ( x _ {j} ) _ {j = 1 } ^ {n} \subset E } \right \} . $$

Then for $ m = 2 $ one has

$$ d ( E) = C ( E) = \ \mathop{\rm exp} \left ( - \lim\limits _ {n \rightarrow \infty } \chi _ {n} ( E) \right ) ; $$

while for $ m \geq 3 $ it is expedient (see [4]) to take

$$ d ( E) = C ( E) = \ { \frac{1}{\lim\limits _ {n \rightarrow \infty } \chi _ {n} ( E) } } . $$

References

[1]	M. Fekete, "Ueber die Verteilung der Wurzeln bei gewissen algebraischen Gleichungen mit ganzzahligen Koeffizienten" Math. Z. , 17 (1923) pp. 228–249
[2]	G. Pólya, G. Szegö, "Ueber den transfiniten Durchmesser (Kapazitätskonstante) von ebenen und räumlichen Punktmengen" J. Reine Angew. Math. , 165 (1931) pp. 4–49
[3]	G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)
[4]	L. Carleson, "Selected problems on exceptional sets" , v. Nostrand (1967)
[5]	V.I. Smirnov, A.N. Lebedev, "Functions of a complex variable" , M.I.T. (1968) (Translated from Russian)
[6]	M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1959)
[7]	R. Kühnau, "Geometrie der konformen Abbildung auf der hyperbolischen und der elliptischen Ebene" , Deutsch. Verlag Wissenschaft. (1974)

Comments

Outer radius is another term for transfinite diameter. See [a1] for a survey on connections between transfinite diameter, Robin constant and capacity in $ \mathbf R ^ {2} $ or $ \mathbf R ^ {n} $.

The notion of transfinite diameter also makes good sense in several complex variables, if interpreted in the correct way: (1) with $ [ a, b] = | a- b | $ is a root of a Vandermondian determinant:

$$ d _ {n} ( E) = ( \max _ {x ^ {( n ) } \in E ^ {n} } | V ( x ^ {(n)} ) | ) ^ {2/n( n- 1) } , $$

where

$$ V( x ^ {(n)} ) = \mathop{\rm det} [ x _ {i} ^ {j} ] _ {\begin{array} {c} i = 1 \dots n \\ j= 0 \dots n- 1 \end{array} } . $$

In $ \mathbf C ^ {n} $, let $ e _ {1} \dots e _ {m _ {n} } $ be an ordered system of monomials of degree $ \leq n $ and let $ x ^ {(n)} $ be a point in $ E ^ {m _ {n} } \subset \mathbf C ^ {m _ {n} } $. Then $ V ( x ^ {(n)} ) $ is defined as $ \mathop{\rm det} [ e _ {i} ( x _ {j} )] $, $ x ^ {n} = ( x _ {1} \dots x _ {m _ {n} } ) $, and $ d _ {n} ( E) = ( \max _ {x ^ {(n)} \in E ^ {m _ {n} } } V( x ^ {(n)} ) ) ^ {1/ \mathop{\rm deg} V( x ^ {n} ) } $. The related capacity is the one associated to the complex Monge–Ampère operator.

References

[a1]	R.E. Kleinman, "On a unified characterization of capacity" J. Král (ed.) J. Lukeš (ed.) J. Veselý (ed.) , Potential theory. Survey and problems (Prague, 1987) , Lect. notes in math. , 1344 , Plenum (1988) pp. 103–120
[a2]	M. Klimek, "Pluripotential theory" , Cambridge Univ. Press (1991)
[a3]	J. Siciak, "Extremal plurisubharmonic functions and capacities in 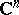" , Sophia Kokyuroku in Math. , 14 , Dept. Math. Sophia Univ. Tokyo (1982)