Totally-irreducible set

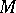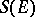A set of linear operators (cf. Linear operator) on a locally convex topological vector space that is everywhere dense in the algebra of all weakly-continuous linear operators on (cf. Weak topology); in this context 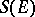is considered with the weak operator topology. The concept of a totally-irreducible set, initially introduced for Banach spaces, also proved useful in the theory of group representations, mainly for semi-simple Lie groups. If 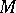is a totally-irreducible set, it is also topologically irreducible, i.e. any closed subspace of 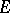which is invariant with respect to coincides with zero or with the entire space 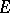. 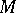If is a totally-irreducible set, its commutator subset in 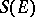consists of the operators that are multiples of the identity. The property of total irreducibility is equivalent to that of topological irreducibility in the following cases: 1) 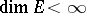; or 2) 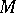is a semi-group of unitary operators on a Hilbert space.

References

[1]	D.P. Zhelobenko, "Harmonic analysis of functions on semi-simple complex Lie groups" , Moscow (1974) (In Russian)

Comments

A set 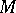of operators on a vector space is algebraically irreducible if there are no proper subspaces of 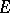(i.e. except 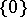and 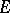) that are invariant under all 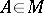. Cf. also Irreducible representation. A totally-irreducible set is also called completely irreducible.

The link between topological irreducibility and algebraic irreducibility and the statement that the commutator subset of consists of multiples of the identity is provided by the Schur lemma. For a finite-dimensional space 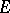over a field 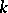, the algebraic (or topological) irreducibility of a set of operators implies that the commutator subset in 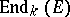is a division algebra over 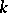in general, and equal to 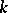if 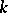is algebraically closed. If 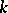is not algebraically closed, this need not be the case. E.g., if , the commutant of an irreducible representation of a group can be 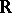, 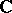or the four-dimensional algebra of quaternions over 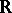. Thus, the statement above about the equivalence for finite-dimensional 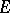between algebraic irreducibility (or, what is the same in this case, topological irreducibility) holds for algebraically closed ground fields but it does not hold for a non-algebraically closed ground field. For instance, if 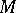is the collection of operators

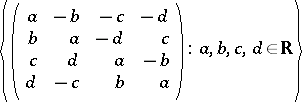(the left regular representation of the quaternion algebra on itself), then 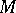is algebraically irreducible, but its commutant algebra is the four-dimensional algebra of all matrices of the form

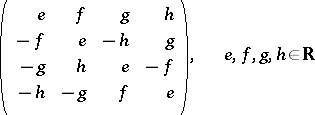(another copy inside 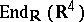of the quaternion algebra, corresponding to the right regular representation).

References

[a1]	O. Bratteli, D.W. Robinson, "Operator algebras and quantum statistical mechanics" , 1 , Springer (1979) pp. 47
[a2]	J. Dixmier, "Les 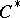-algèbres et leur représentations" , Gauthier-Villars (1964) pp. §2.3