Sturm-Liouville problem
A problem generated by the following equation, where $ x $
varies in a given finite or infinite interval $ ( a, b) $,
$$ \tag{1 } - \frac{d}{dx} \left ( p( x) \frac{dy}{dx} \right ) + l( x) y = \lambda r( x) y, $$
together with some boundary conditions, where $ p( x) $ and $ r( x) $ are positive, $ l( x) $ is real and $ \lambda $ is a complex parameter. Serious studies of this problem were started by J.Ch. Sturm and J. Liouville. The methods and notions that originated during studies of the Sturm–Liouville problem played an important role in the development of many directions in mathematics and physics. It was and remains a constant source of new ideas and problems in the spectral theory of operators and in related problems in analysis. Recently it gained even greater significance, when its relation to certain non-linear evolution equations of mathematical physics were discovered.
If $ p( x) $ is differentiable and $ p( x) r( x) $ is twice differentiable, then, by a substitution, equation (1) can be reduced to (see [1])
$$ \tag{2 } - y ^ {\prime\prime} + q( x) y = \lambda y. $$
It is customary to distinguish between regular and singular problems. A Sturm–Liouville problem for equation (2) is called regular if the interval $ ( a, b) $ in which $ x $ varies is finite and if the function $ q( x) $ is summable on the entire interval $ ( a, b) $. If the interval $ ( a, b) $ is infinite or if $ q( x) $ is not summable (or both), then the problem is called singular.
Below the following possibilities will be considered in some detail: 1) the interval $ ( a, b) $ is finite (in this case, without loss of generality, one may assume $ a= 0 $ and $ b= \pi $); 2) $ a= 0 $, $ b= \infty $; or 3) $ a= - \infty $, $ b = \infty $.
$ 1 $. Consider the problem given on the interval $ [ 0, \pi ] $ by equation (2) and the separated boundary conditions
$$ \tag{3 } y ^ \prime ( 0) - hy( 0) = 0,\ \ y ^ \prime ( \pi ) + Hy ( \pi ) = 0, $$
where $ q( x) $ is a real summable function on $ [ 0, \pi ] $, $ h $ and $ H $ are arbitrary finite or infinite fixed real numbers and $ \lambda $ is a complex parameter. If $ h = \infty $ $ ( H = \infty ) $, then the first (second) condition in (3) is replaced by $ y( 0) = 0 $ $ ( y( \pi ) = 0) $. To be specific it is further assumed that all numbers occurring in the boundary conditions are finite.
The number $ \lambda _ {0} $ is called an eigenvalue for the problem (2), (3) if for $ \lambda = \lambda _ {0} $ equation (2) has a non-trivial solution $ y _ {0} ( x) \not\equiv 0 $ that satisfies (3); the function $ y _ {0} ( x) $ is then called the eigenfunction corresponding to the eigenvalue $ \lambda _ {0} $.
The eigenvalues for the boundary value problem (2), (3) are real; to the distinct eigenvalues correspond linearly independent eigenfunctions (since $ q( x) $ and the numbers $ h, H $ are real, the eigenfunctions for the problem (2), (3) can be chosen to be real); eigenfunctions $ y _ {1} ( x) $ and $ y _ {2} ( x) $ corresponding to different eigenvalues are unique and orthogonal, i.e. $ \int _ {0} ^ \pi y _ {1} ( x) y _ {2} ( x) dx = 0 $.
There exists an unboundedly-increasing sequence of eigenvalues $ \lambda _ {0} , \lambda _ {1} ,\dots $ for the boundary value problem (2), (3); moreover, the eigenfunction $ y _ {n} ( x) $ corresponding to the eigenvalue $ \lambda _ {n} $ has precisely $ n $ zeros in the interval $ ( 0, \pi ) $.
Let $ W _ {2} ^ {m} [ 0, \pi ] $ be the Sobolev space of complex-valued functions on the interval $ [ 0, \pi ] $ that have $ m- 1 $ absolutely-continuous derivatives and with $ m $- th derivatives summable on $ [ 0, \pi ] $. If $ q \in W _ {2} ^ {m} [ 0, \pi ] $, then the eigenvalues $ \lambda _ {n} $ of the boundary value problem (2), (3) for large $ n $ satisfy the following asymptotic equation (see [4]):
$$ \sqrt {\lambda _ {n} } = n + \sum _ {1\leq 2j+ 1\leq m+ 2 } \frac{c _ {2j+1} }{n ^ {2j+1}} + $$
$$ + \frac{(- 1) ^ {m-1} }{2 ^ {m+2}} \left ( S _ {m} ( n) + \frac{\widetilde{S} _ {m} ( n) }{n} \right ) \frac{1}{n ^ {m+1} } + \frac{\delta _ {n} }{n ^ {m+2} } + \frac{\epsilon _ {n} ( h, H) }{n ^ {m+2} } , $$
where $ c _ {2j+1} $ are numbers independent of $ n $,
$$ c _ {1} = \frac{1} \pi \left ( h + H + \frac{1}{2} \int\limits _ { 0 } ^ \pi q( t) dt \right ) , $$
$$ S _ {m} ( n) = \frac{2} \pi \int\limits _ { 0 } ^ \pi q ^ {(m)} ( t) \sin \left \{ 2nt - \frac \pi {2} ( m+ 1) \right \} dt, $$
$$ \widetilde{S} _ {m} ( n) = \frac{2} \pi \int\limits _ { 0 } ^ \pi q ^ {(m)} ( t) ( 2h- c _ {1} t) \sin \left \{ 2nt - \frac \pi {2} ( m+ 2) \right \} dt, $$
$ \delta _ {n} $ does not depend on $ h, H $, and
$$ \sum_{n=0}^ \infty | \delta _ {n} | ^ {2} < \infty ,\ \ \sum_{n=0}^ \infty | \epsilon _ {n} ( h, H) | ^ {2} < \infty . $$
The above implies, in particular, that if $ q \in W _ {2} ^ {1} [ 0, \pi ] $, then
$$ \lambda _ {n} = n ^ {2} + c + \frac{\gamma _ {n} }{n} , $$
where
$$ c = \frac{2} \pi \left ( h+ H+ \frac{1}{2} \int\limits _ { 0 } ^ \pi q( t) dt \right ) ,\ \ \sum_{n=0}^ \infty | \gamma _ {n} | ^ {2} < \infty . $$
Thus, the series $ \sum_{n=0}^ \infty ( \lambda _ {n} - n ^ {2} - c) $ is convergent. Its sum is called the regularized trace of the problem (2), (3) (see [13]):
$$ \sum_{n=0}^ \infty ( \lambda - n ^ {2} - c) = \ \frac{q( 0)+ q( \pi ) }{4} - \frac{( h+ H) ^ {2} }{2} + hH - \frac{c}{2} . $$
Let $ v _ {0} ( x), v _ {1} ( x) \dots $ be the orthonormal eigenfunctions of the problem (2), (3) corresponding to the eigenvalues $ \lambda _ {0} , \lambda _ {1} ,\dots $. For any function $ f \in L _ {2} [ 0, \pi ] $ the so-called Parseval equality holds:
$$ \int\limits _ { 0 } ^ \pi | f( x) | ^ {2} dx = \sum_{n=0}^ \infty | a _ {n} | ^ {2} , $$
where
$$ a _ {n} = \int\limits _ { 0 } ^ \pi f( x) v _ {n} ( x) dx, $$
and the following formula for eigenfunction expansion is valid:
$$ \tag{4 } f( x) = \sum_{n=0}^ \infty a _ {n} v _ {n} ( x), $$
where the series converges in the metric of $ L _ {2} [ 0, \pi ] $. Completeness and expansion theorems for a regular Sturm–Liouville problem were first proved by V.A. Steklov [14].
If the function $ f $ has a continuous second derivative and satisfies the boundary conditions (3), then the following assertions hold (see [15]):
a) the series (4) converges absolutely and uniformly on $ [ 0, \pi ] $ to $ f( x) $;
b) the once-differentiated series (4) converges absolutely and uniformly on $ [ 0, \pi ] $ to $ f ^ { \prime } ( x) $;
c) at any point where $ f ^ { \prime\prime } ( x) $ satisfies some local condition of expansion in a Fourier series (e.g. is of bounded variation), the twice-differentiated series (4) converges to $ f ^ { \prime\prime } ( x) $.
For any function $ f \in L _ {1} [ 0, \pi ] $ the series (4) is uniformly equiconvergent with the Fourier cosine series of $ f $, i.e.
$$ \lim\limits _ {N \rightarrow \infty } \sup _ {0 \leq x \leq \pi } | V _ {N,f} ( x) - c _ {N,f} ( x) | = 0, $$
where
$$ V _ {N,f} ( x) = \int\limits _ { 0 } ^ \pi f( t) \sum_{n=0}^ { N } v _ {n} ( x) v _ {n} ( t) dt, $$
$$ c _ {N,f} ( x) = \int\limits _ { 0 } ^ \pi f( t) \left \{ \frac{1} \pi + \frac{2} \pi \sum_{n=1}^N \cos nx \cos nt \right \} dt. $$
This means that the expansion of $ f $ with respect to the eigenfunctions of the boundary value problem (2), (3) converges under the same conditions as the expansion of $ f $ in a Fourier cosine series (see [1], [4]).
$ 2 $. The differential equation (2) is considered on the half-line $ 0 \leq x < \infty $ with a boundary condition at zero:
$$ \tag{5 } y ^ \prime ( 0) - hy( 0) = 0. $$
The function $ q $ is assumed to be real and summable on any finite subinterval of $ [ 0, \infty ) $ and $ h $ is assumed to be real.
Let $ \phi ( x, \lambda ) $ be a solution of (2) with the initial conditions $ y( 0) = 1 $, $ y ^ \prime ( 0) = h $( so that $ \phi ( x, \lambda ) $ satisfies also the boundary condition (5)). Let $ f $ be any function from $ L _ {2} ( 0, \infty ) $ and let $ \Phi _ {f,b } ( x) = \int _ {0} ^ {b} f( x) \phi ( x, \lambda ) dx $, where $ b $ is an arbitrary finite positive number. For any function $ q $ and any number $ h $ there is at least one decreasing function $ \rho ( \lambda ) $, $ - \infty < \lambda < \infty $, independent of $ f $, that has the following properties:
a) there is a function $ \Phi _ {f} ( \lambda ) $, which is the limit of $ \Phi _ {f,b} ( \lambda ) $ for $ b \rightarrow \infty $ in the metric of $ L _ {2, \rho } (- \infty , \infty ) $( the space of $ \rho $- measurable functions $ \psi ( \lambda ) $ for which $ \| \psi \| ^ {2} = \int _ {- \infty } ^ \infty | \psi ( \lambda ) | ^ {2} d \rho ( \lambda ) < \infty $), i.e.
$$ \lim\limits _ {b \rightarrow \infty } \int\limits _ {- \infty } ^ \infty | \Phi _ {f} ( \lambda ) - \Phi _ {f,b } ( \lambda ) | ^ {2} d \rho ( \lambda ) = 0; $$
b) the Parseval equality is valid:
$$ \int\limits _ { 0 } ^ \infty | f( x) | ^ {2} dx = \ \int\limits _ {- \infty } ^ \infty | \Phi _ {f} ( \lambda ) | ^ {2} d \rho ( \lambda ). $$
The function $ \rho ( \lambda ) $ is called the spectral function (or spectral density) for the boundary value problem (2), (5) (see [9]–[11]).
For the spectral function $ \rho ( \lambda ) $ of the problem (2), (5) the following asymptotic formula is true (see [16]) (for a more precise form, see ):
$$ \lim\limits _ {\lambda \rightarrow - \infty } e ^ {\sqrt \lambda x } ( \rho ( \lambda ) - \rho (- \infty )) = 0,\ \ 0 \leq x < \infty , $$
$$ \lim\limits _ {\lambda \rightarrow \infty } \left ( \rho ( \lambda ) - \rho (- \infty ) - \frac{2} \pi \sqrt \lambda + h \right ) = 0. $$
The following equiconvergence theorem is valid : For an arbitrary function $ f \in L _ {2} ( 0, \infty ) $, let
$$ \Phi _ {f} ( \lambda ) = \int\limits _ { 0 } ^ \infty f( x) \phi ( x, \lambda ) dx, $$
$$ C _ {f} ( \lambda ) = \int\limits _ { 0 } ^ \infty f( x) \cos \sqrt \lambda x dx $$
(the integrals converge in the metrics of $ L _ {2, \rho } (- \infty , \infty ) $ and $ L _ {2, \sqrt \lambda } ( 0, \infty ) $, respectively); then for any fixed $ b < \infty $ the integral
$$ \int\limits _ {- \infty } ^ { b } \Phi _ {f} ( \lambda ) \phi ( x, \lambda ) d \rho ( \lambda ) $$
converges absolutely and uniformly with respect to $ x \in [ 0, b] $, and
$$ \lim\limits _ {N \rightarrow \infty } \sup _ {0 \leq x < b } \ \left | \int\limits _ {- \infty } ^ { N } \Phi _ {f} ( \lambda ) \phi ( x, \lambda ) d \rho ( \lambda ) \right . - $$
$$ - \left . \frac{2} \pi \int\limits _ { 0 } ^ { N } C _ {f} ( \lambda ) \cos \sqrt \lambda x d \sqrt \lambda \right | = 0. $$
Let problem (2), (5) have a discrete spectrum, i.e. let its spectrum consist of a countable number of eigenvalues $ \lambda _ {1} < \lambda _ {2} < \dots $ with a unique limit point at infinity. Under certain restrictions on the function $ q $, for the function $ N( \lambda ) = \sum _ {\lambda _ {n} < \lambda } 1 $, i.e. the number of eigenvalues less than $ \lambda $, the following asymptotic formula is valid:
$$ N( \lambda ) \sim \frac{1}{2 \pi } \int\limits _ {q( x) < \lambda } ( \lambda - q( x)) ^ {1/2} dx. $$
Simultaneously with $ \phi ( x, \lambda ) $, a second solution $ \theta ( x, \lambda ) $ of equation (2) is introduced, satisfying the conditions $ \theta ( 0, \lambda ) = 0 $, $ \theta ^ \prime ( 0, \lambda ) = 1 $, so that $ \phi ( x, \lambda ) $ and $ \theta ( x, \lambda ) $ form a fundamental system of solutions of (2). For a fixed $ \lambda $ $ ( \mathop{\rm Im} \lambda \neq 0) $ and $ b > 0 $ the following fractional-linear function is considered:
$$ w _ {\lambda ,b } = w _ {\lambda ,b } ( t) = \ \frac{- \theta ^ \prime ( b, \lambda )- t \theta ( b, \lambda ) }{\phi ^ \prime ( b,\ \lambda ) + t \phi ( b, \lambda ) } . $$
When the independent variable $ t $ varies on the real line, the point $ w _ {\lambda ,b } $ describes a circle bounding a disc $ K _ {\lambda ,b } $. It always lies in the same half-plane (lower or upper) as $ \lambda $. When $ b $ increases, $ K _ {\lambda ,b } $ shrinks, i.e. for $ b < b ^ \prime $ the disc $ K _ {\lambda ,b\prime } $ lies entirely inside the disc $ K _ {\lambda ,b } $. There is (for $ b \rightarrow \infty $) a limit disc or a point $ K _ {\lambda , \infty } $; if
$$ \tag{6 } \int\limits _ { 0 } ^ \infty | \phi ( x, \lambda ) | ^ {2} dx < \infty , $$
then $ K _ {\lambda , \infty } $ is a disc, otherwise it is a point (see [10]). If condition (6) is fulfilled for some non-real value of $ \lambda $, then it is fulfilled for all values of $ \lambda $. In the case of a limit disc, for any value of $ \lambda $ all solutions of (2) belong to $ L _ {2} ( 0, \infty ) $, and in the case of a limit point, for any non-real value of $ \lambda $ this equation has the solution $ \theta ( x, \lambda ) + m( \lambda ) \phi ( x, \lambda ) $, which belongs to $ L _ {2} ( 0, \infty ) $, where $ m( \lambda ) $ is the limit point $ ( m( \lambda ) = K _ {\lambda , \infty } ) $.
If $ q( x) \geq - cx ^ {2} $, where $ c $ is some positive constant, then the case of a limit point holds (see [19]); for more general results see [20], [21].
$ 3 $. Consider now equation (2) on the whole line $ - \infty < x < \infty $ under the assumption that $ q( x) $ is a real summable function on every finite subinterval of $ (- \infty , \infty ) $. Let $ \phi _ {1} ( x, \lambda ) $, $ \phi _ {2} ( x, \lambda ) $ be the solutions of (2) satisfying the conditions $ \phi _ {1} ( 0, \lambda ) = \phi _ {2} ^ \prime ( 0, \lambda ) = 1 $, $ \phi _ {1} ^ \prime ( 0, \lambda ) = \phi _ {2} ( 0, \lambda ) = 0 $.
There is at least one real symmetric non-decreasing matrix-function
$$ {\mathcal P} ( \lambda ) = \left \| \begin{array}{ll} \rho _ {11} ( \lambda ) &\rho _ {12} ( \lambda ) \\ \rho _ {21} ( \lambda ) &\rho _ {22} ( \lambda ) \\ \end{array} \right \| ,\ \ - \infty < \lambda < \infty , $$
with the following properties:
a) for any function $ f \in L _ {2} (- \infty , \infty ) $ there exist functions $ \Phi _ {j,f} ( \lambda ) $, $ j = 1, 2 $, defined by
$$ \Phi _ {j,f} ( \lambda ) = {\textrm{ l } \cdot \textrm{ i } \cdot \textrm{ m } } _ {b \rightarrow \infty } \int\limits _ {-b} ^ { b } f( x) \phi _ {j} ( x, \lambda ) dx,\ \ j = 1, 2 , $$
where the limit is in the metric of $ L _ {2, {\mathcal P} } (- \infty , \infty ) $;
b) the Parseval equality is valid:
$$ \int\limits _ {- \infty } ^ \infty | f( x) | ^ {2} dx = \ \sum_{ j,k=1}^ { 2 } \int\limits _ {- \infty } ^ \infty \Phi _ {j,f} ( \lambda ) {\Phi _ {k} ( \lambda ) } bar d \rho _ {jk} ( \lambda ). $$
References
| [1] | B.M. Levitan, I.S. Sargsyan, "An introduction to spectral theory" , Amer. Math. Soc. (1975) (Translated from Russian) |
| [2] | B.M. Levitan, "Eigenfunction expansions of second-order differential equations" , Moscow-Leningrad (1950) (In Russian) |
| [3] | B.M. Levitan, "Generalized translation operators and some of their applications" , Israel Program Sci. Transl. (1964) (Translated from Russian) |
| [4] | V.A. Marchenko, "Sturm–Liouville operators and applications" , Birkhäuser (1986) (Translated from Russian) |
| [5] | E.C. Titchmarsh, "Eigenfunction expansions associated with second-order differential equations" , 1 , Clarendon Press (1962) |
| [6] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17 |
| [7] | M.A. Naimark, "Lineare Differentialoperatoren" , Akademie Verlag (1960) (Translated from Russian) |
| [8] | A.G. Kostyuchenko, I.S. Sargsyan, "Distribution of eigenvalues" , Moscow (1979) (In Russian) |
| [9] | H. Weyl, "Über gewöhnliche lineare Differentialgleichungen mit singulären Stellen und ihre Eigenfunktionen" Gött. Nachr. (1909) pp. 37–64 |
| [10] | H. Weyl, "Über gewöhnliche lineare Differentialgleichungen mit Singularitäten und die Zugehörigen Entwicklungen willküriger Funktionen" Math. Ann. , 68 (1910) pp. 220–269 |
| [11] | H. Weyl, "Über gewöhnliche lineare Differentialgleichungen mit singulären Stellen und ihre Eigenfunktionen (2)" Gött. Nachr. (1910) pp. 442–467 |
| [12] | M.G. Krein, "On the indeterminate case of the Sturm–Liouville boundary problem in the interval 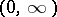 " Izv. Akad. Nauk SSSR Ser. Mat. , 16 : 4 (1952) pp. 293–324 (In Russian) " Izv. Akad. Nauk SSSR Ser. Mat. , 16 : 4 (1952) pp. 293–324 (In Russian) |
| [13] | I.M. Gel'fand, B.M. Levitan, "On a simple identity for the characteristic values of a differential operator of the second order" Dokl. Akad. Nauk SSSR , 88 : 4 (1953) pp. 593–596 (In Russian) |
| [14] | V.A. Steklov, "On the development of a given function in a series made up from harmonic functions" Soobshch. Khar'k. Mat. Obshch. , 5 : 1–2 (1896) (In Russian) |
| [15] | B.M. Levitan, I.S. Sargsyan, "Some problems in the theory of the Sturm–Liouville equation" Russian Math. Surveys , 15 : 1 (1960) pp. 1–95 Uspekhi Mat. Nauk , 15 : 1 (1960) pp. 3–98 |
| [16] | V.A. Marchenko, "On the theory of a second-order differential operator" Dokl. Akad. Nauk SSSR , 72 : 3 (1950) pp. 457–460 (In Russian) |
| [17a] | B.M. Levitan, "On the asymptotic behaviour of the spectral function of a second-order self-adjoint differential equation, and on eigenfunction expansion" Izv. Akad. Nauk SSSR Ser. Mat. , 17 : 4 (1953) pp. 331–364 (In Russian) |
| [17b] | B.M. Levitan, "On the asymptotic behaviour of the spectral function of a second-order self-adjoint differential equation, and on eigenfunction expansion II" Izv. Akad. Nauk SSSR Ser. Mat. , 19 : 1 (1955) pp. 33–58 (In Russian) |
| [18] | J.S. de Wet, F. Mandl, "On the asymptotic distribution of eigenvalues" Proc. Roy. Soc. Ser. A , 200 (1950) pp. 572–580 |
| [19] | E. Titchmarsh, "On the uniqueness of the Green's function associated with a second-order differential equation" Canad. J. Math. , 1 (1949) pp. 191–198 |
| [20] | N. Levinson, "Criteria for the limit-point case for second order linear differential operators" Časopis Pěst Mat. Fys. , 74 (1949) pp. 17–20 |
| [21] | D. Sears, E. Titchmarsh, "Some eigenfunction formulae" Quart. J. Math. (Oxford Ser.) , 1 (1950) pp. 165–175 |
Comments
Eigenvalue problems of type (2) and the corresponding inverse problems (cf. Sturm–Liouville problem, inverse) play a major role in solving soliton equations, cf. Soliton, by the so-called "inverse-scattering methodinverse scattering method" . Cf. Korteweg–de Vries equation for a description of this method, and/or e.g. [a1]–[a5].
In the West one usually considers the boundary of $ K _ {\lambda ,b } $, and speaks of the limit point and limit circle cases.
References
| [a1] | P.D. Lax, "Integrals of nonlinear equations of evolution and solitary waves" Comm. Pure Appl. Math. , 21 (1968) pp. 467–490 |
| [a2] | V.E. Zakharov, A.B. Shabat, Soviet Phys. JETP (1972) pp. 62–69 |
| [a3] | R.M. Miura, "The Korteweg–de Vries equation: a survey of results" SIAM Review , 18 (1976) pp. 412–459 |
| [a4] | W. Eckhaus, A. van Harten, "The inverse scattering transformation and the theory of solitons" , North-Holland (1983) |
| [a5] | P.C. Schuur, "Asymptotic analysis of soliton problems" , Springer (1986) |
| [a6] | Yu.M. [Yu.M. Berezanskii] Berezanskiy, "Expansions in eigenfunctions of selfadjoint operators" , Amer. Math. Soc. (1968) (Translated from Russian) |
| [a7] | W.T. Reid, "Sturmian theory for ordinary differential equations" , Springer (1980) |
Sturm-Liouville problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sturm-Liouville_problem&oldid=55171