Stepwise semantic system
A variant of constructive semantics proposed by A.A. Markov [2], . In the construction of this system, particular attention is paid to one of the problems of semantics — the constructive interpretation of implication. The traditional intuitionistic explanation of the meaning of the statement $ ( A \supset B) $
is that $ ( A \supset B) $
expresses the realizability of a construction $ p $,
such that if $ q $
is an arbitrary construction asserting $ A $,
then $ p $
and $ q $
together make it possible to find a construction that asserts $ B $.
This informal explanation does not lend itself to an exact definition, for a number of reasons. Markov's idea is that the implication $ ( A \supset B) $
can be considered as a formulation of a statement on the deducibility of $ B $
from the premise $ A $
by means of a theory containing a principle of infinite induction (a semi-formal theory). The semi-formal theory in question, as well as the semantics of the formulas $ A $
and $ B $,
can therefore be explained at an earlier stage of the construction. As a result a stepwise semantic system arises, in which the sense of the formulas of the next step is defined in terms of the objects of the previous step.
Markov constructed two equivalent variants of a stepwise semantic system — the "long tower stepwise semantic system03B10long tower" [2] and the "short tower stepwise semantic system03B20short tower" . The short-tower variant is briefly explained below in the traditional notation of predicate calculus as well as in the language of formal arithmetic (cf. Arithmetic, formal) (Markov himself used a notation of formulas without brackets). The elementary formulas of the language $ L _ {0} $ take either the form $ ( t= r) $ or $ ( t \neq r) $, where $ t, r $ are primitive recursive terms (terms of $ L _ {0} $). The other formulas of $ L _ {0} $ are constructed in the usual way using the logical operations of conjunction $ \wedge $, disjunction $ \lor $ and the restricted quantifiers (cf. Restricted quantifier) $ (\forall x \leq t) \phi $, $ (\exists x \leq t) \phi $, where $ \phi $ is a formula in $ L _ {0} $ and $ t $ is a term in $ L _ {0} $. The language $ L _ {0} $ is decidable in the sense that there is a general method of recognizing the true closed formulas of $ L _ {0} $ out of all the formulas of $ L _ {0} $. The semantics of the formulas of $ L _ {0} $ is defined by induction with respect to the construction of the formula. Every formula of $ L _ {0} $ is equivalent to a formula without quantifiers.
The formulas of $ L _ {1} $ are constructed from the formulas of $ L _ {0} $ by means of any number of uses of the operations $ \lor $, $ \wedge $ and the existential quantifier. The language $ L _ {1} $ is undecidable, but a calculus $ C $ can be constructed in which exactly the true closed formulas of $ L _ {1} $ are derivable. The formulas of $ L _ {2} $ are constructed inductively from the formulas of $ L _ {1} $ by means of a single application of the operation $ \supset $ and any number of applications of the conjunction $ \wedge $ and the quantifier $ \forall $. Thus, the formulas of $ L _ {2} $ take one of the following forms: 1) the formulas of $ L _ {1} $; 2) $ ( \phi \wedge \psi ) $, where $ \phi , \psi $ are formulas of $ L _ {2} $; 3) $ ( \alpha \supset \beta ) $, where $ \alpha , \beta $ are formulas of $ L _ {1} $; 4) $ \forall x \phi $, where $ \phi $ is a formula of $ L _ {2} $. The implications $ ( \alpha \supset \beta ) $ are interpreted as follows: $ ( \alpha \supset \beta ) $ expresses the presence of a general method which, for any word $ Q $ in the alphabet of the language, makes it possible either to establish that $ Q $ is not a deduction of the formula $ \alpha $ in the calculus $ C $, or to give a deduction of $ \beta $ in the calculus $ C $. A semi-formal theory $ S _ {2} $ is then constructed in which the closed formulas of $ L _ {2} $ can be deduced (for $ L _ {1} $, the role of $ S _ {2} $ is played by $ C $). The true formulas of $ L _ {2} $ are the axioms of $ S _ {2} $. Among the usual derivation rules is the effective $ \omega $- rule with an infinite number of premises: If a general method exists that enables one to derive the formula $ \phi ( n) $ in $ S _ {2} $ for every natural number $ n $, then the formula $ \forall x \phi ( x) $ can be considered to be derivable in $ S _ {2} $. The soundness of $ S _ {2} $ is expressed by the following theorem: Every closed formula of $ L _ {2} $ that can be derived from a true formula of $ L _ {2} $ or from a premise, is true in $ L _ {2} $.
The formulas of $ L _ {3} $ can be constructed inductively from $ L _ {2} $ by means of a single application of the operation $ \supset _ {1} $ and any number of applications of $ \wedge $ and $ \forall $. The implication $ ( \alpha \supset _ {1} \beta ) $ expresses the fact that $ \beta $ is derivable from the formula $ \alpha $ in the theory $ S _ {2} $. It can be shown that the two forms of implication in the language $ L _ {3} $ are consistent with each other when they are both applicable. The semi-formal theory $ S _ {3} $ is then constructed, and its soundness is proved. The languages $ L _ {4} , L _ {5} \dots $ are constructed in the same way, as are the semi-formal theories $ S _ {4} , S _ {5} , . . . $. The formulas of $ L _ {n+} 1 $ are constructed from the formulas of $ L _ {n} $ by means of a single application of the operation $ \supset _ {(} n- 1) $ to formulas of the previous language $ L _ {n} $ and of any number of applications of $ \wedge $ and $ \forall $ to the formulas of $ L _ {n+} 1 $. The implication $ ( \alpha \supset _ {(} n- 1) \beta ) $ expresses the fact that $ \beta $ is derivable from $ \alpha $ in $ S _ {n} $. All $ S _ {n} $ are sound: Every closed formula of $ L _ {n} $ that can be derived from a true formula is true. Implications at different levels are consistent when they are both applicable.
This consistency makes it possible to combine all the languages $ L _ {n} $ in a single language $ L _ \omega $, whose formulas are obtained if the indices are removed from the implications in all the languages $ L _ {n} $. A formula $ \phi $ of $ L _ \omega $ is considered to be true if it is true in some $ L _ {n} $, where the indices of the implications are chosen so as to make $ \phi $ into a formula of $ L _ {n} $.
If the negation $ \neg \phi $ is introduced in $ L _ \omega $ as a shorthand notation for $ ( \phi \supset 0 = 1) $, then the formula $ \neg \neg \alpha \supset \alpha $ is true in $ L _ \omega $ for every formula $ \alpha $ of the language $ L _ {1} $. Thus, the constructive selection principle proves to be true in $ L _ \omega $. The languages $ L _ {n} $ form an essentially non-degenerate hierarchy from the point of view of the expressive possibilities of their formulas. Classical predicate calculus with the operations $ \wedge $, $ \neg $, $ \supset $, $ \forall $ is complete with respect to truth in $ L _ \omega $.
Finally, $ L _ {\omega + 1 } $ contains all formulas of formal arithmetic. Using the algorithm exposing Shanin's constructive problem [4], every closed formula $ \phi $ of $ L _ {\omega + 1 } $ can be reduced to the form $ \exists x \psi ( x) $, where $ \psi ( x) $ is a formula of $ L _ \omega $. A formula $ \phi $ is considered to be true if a natural number $ n $ can be given such that $ \phi ( n) $ is true in $ L _ \omega $. This concept of the judgements of arithmetic is consistent with all the fundamental principles of constructive mathematics. In particular, every formula of $ L _ {\omega + 1 } $ is equivalent to its proper recursive Kleene realization [5].
References
| [1] | A. Heyting, "Intuitionism: an introduction" , North-Holland (1970) |
| [2] | A.A. Markov, "Essai de construction d'une logique de la mathématique constructive. Logique et méthodologie des sciences en U.R.S.S." Rev. Internat. Phil. , 25 : 4 (1971) pp. 477–507 |
| [3a] | A.A. Markov, "On the language 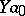 " Soviet Math. Dokl. , 15 (1974) pp. 38–42 Dokl. Akad. Nauk SSSR , 214 : 1 (1974) pp. 40–43 " Soviet Math. Dokl. , 15 (1974) pp. 38–42 Dokl. Akad. Nauk SSSR , 214 : 1 (1974) pp. 40–43 |
| [3b] | A.A. Markov, "On the language 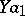 " Soviet Math. Dokl. , 15 (1974) pp. 125–128 Dokl. Akad. Nauk SSSR , 214 : 2 (1974) pp. 279–282 " Soviet Math. Dokl. , 15 (1974) pp. 125–128 Dokl. Akad. Nauk SSSR , 214 : 2 (1974) pp. 279–282 |
| [3c] | A.A. Markov, "On the language 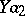 " Soviet Math. Dokl. , 15 (1974) pp. 184–188 Dokl. Akad. Nauk SSSR , 214 : 3 (1974) pp. 513–516 " Soviet Math. Dokl. , 15 (1974) pp. 184–188 Dokl. Akad. Nauk SSSR , 214 : 3 (1974) pp. 513–516 |
| [3d] | A.A. Markov, "On the language 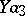 " Soviet Math. Dokl. , 15 (1974) pp. 242–246 Dokl. Akad. Nauk SSSR , 214 : 4 (1974) pp. 765–768 " Soviet Math. Dokl. , 15 (1974) pp. 242–246 Dokl. Akad. Nauk SSSR , 214 : 4 (1974) pp. 765–768 |
| [3e] | A.A. Markov, "On the languages 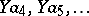 " Soviet Math. Dokl. , 15 (1974) pp. 313–318 Dokl. Akad. Nauk SSSR , 214 : 5 (1974) pp. 1031–1034; 1262–1264 " Soviet Math. Dokl. , 15 (1974) pp. 313–318 Dokl. Akad. Nauk SSSR , 214 : 5 (1974) pp. 1031–1034; 1262–1264 |
| [3f] | A.A. Markov, "On the language 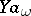 " Soviet Math. Dokl. , 15 (1974) pp. 443–447 Dokl. Akad. Nauk SSSR , 215 : 1 (1974) pp. 57–60 " Soviet Math. Dokl. , 15 (1974) pp. 443–447 Dokl. Akad. Nauk SSSR , 215 : 1 (1974) pp. 57–60 |
| [3g] | A.A. Markov, "On the completeness of the classical predicate calculus in constructive mathematics" Soviet Math. Dokl. , 15 (1974) pp. 476–481 Dokl. Akad. Nauk SSSR , 215 : 2 (1974) pp. 266–269 |
| [4] | N.A. Shanin, "On the constructive interpretation of mathematical judgements" Transl. Amer. Math. Soc. (2) , 23 (1960) pp. 109–190 Trudy Mat. Inst. Steklov. , 52 (1958) pp. 226–311 |
| [5] | A.G. Dragalin, "Mathematical intuitionism. Introduction to proof theory" , Amer. Math. Soc. (1988) (Translated from Russian) |
Comments
References
| [a1] | A.A. Markov, N.M. [N.M. Nagornyi] Nagorny, "The theory of algorithms" , Kluwer (1988) pp. §16 (Translated from Russian) |
Stepwise semantic system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stepwise_semantic_system&oldid=48835