Statistical quality control
A branch of mathematical statistics, the methods of which are used in industry to determine the level of quality actually attained, the trends which affect it and its influence on the industrial process. The quality of mass production is characterized by the totality of properties that can be represented in the form of a set of numbers or functions. In the USSR, the required level of quality is defined by State Standards; standards of quality can also be prescribed in other ways. These standards provide rules governing the actual level of quality indicators. It is necessary to use these standards, since the decisions taken as a result of the control are related to real expenditure and infringe upon the interests of industrial companies. The methods of statistical quality control play an important role in the general system of measures taken to control the quality of mass production. This is primarily caused by the fact that the variability of numerical characteristics of basic quality indicators is random by nature. Attempts to make the control more objective and free of systematic errors make it necessary to use methods of randomization, which in turn makes it necessary to use probabilistic and statistical methods.
The mathematical methods used in statistical quality control are numerous. The most common are methods of continuous monitoring of mass production in the manufacturing process, with the aim of detecting unwanted deviations and the need for appropriate adjustments of the machinery.
Let $ \{ O _ {t} \} $ be a sequence of items, $ t = 1, 2 ,\dots $. As a result of the control, the number $ \epsilon _ {t} $ is associated with the item $ O _ {t} $. Under a control using an alternative test, $ \epsilon _ {t} = 0 $ if $ O _ {t} $ is acceptable and $ \epsilon _ {t} = 1 $ if $ O _ {t} $ is defective. Defective items are excluded. Control using Dodge plans $ \pi ( f, i) $ is defined by the following system of rules. The control begins with a total inspection of the items in the sequence $ \{ O _ {t} \} $, and continues until a series of $ i $ acceptable items is found. Every subsequent item is chosen for control randomly, with probability $ f $, $ 0 < f < 1 $. As soon as a defective item is discovered, the control starts again, continuing until a series of $ i $ acceptable items is found. As before, a sampling control then follows with probability $ f $, etc. For example, let $ \{ \epsilon _ {t} \} $ be a Bernoulli sequence, $ {\mathsf P} \{ \epsilon _ {t} = 1 \} = q $( cf. Bernoulli trials). The mean proportion of controlled items using the plan $ \pi ( f, i) $ is then equal to
$$ f(q) = f[f + (1-f)(1-q)^{i}] ^ {-1} . $$
By choosing suitable values of $ f $ and $ i $, the value of the average output quality level
$$ L ^ \star = \max _ {0 \leq q \leq 1 } L( q) $$
is used, where
$$ L( q) = \frac{q[ 1- f( q)] }{1- q f( q) } $$
is the conditional probability that the item will prove to be defective given that it has not yet been controlled (see [1], [2]).
In cases where the control of the sequence of times $ \{ O _ {t} \} $ is carried out through a quantitative characteristic, the values $ \epsilon _ {t} $ of the results of the control are considered as a stochastic process. Basically, the USSR State Standards proceed from the hypothesis that if there are no discrepancies in the values of $ \{ \epsilon _ {t} \} $, a sequence of mutually-independent normally-distributed stochastic variables is formed. The testing of the initial hypothesis on the type of distribution law of $ \epsilon _ {t} $ is a necessary preliminary condition for the efficient use of control through a quantitative characteristic. If there are discrepancies, this will lead either to the appearance of a trend — a systematic rise (or fall) in the mean values of $ \epsilon _ {t} $, to an increase in the variance of $ \epsilon _ {t} $, etc. In detecting similar discrepancies, methods making use of control charts are widely used. UCB LCB signal for adjustment
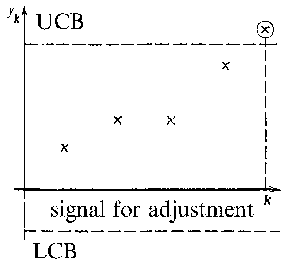
Figure: s087460a
In control charts (see Fig.), on the $ x $- axis a label $ k $ is given, representing the controlled sampling $ O _ {t _ {k} + 1 } \dots O _ {t _ {k} + n } $, and on the $ y $- axis the value of the variable $ y _ {k} $, defined by the values $ \epsilon _ {t _ {k} + 1 } = x _ {1} \dots \epsilon _ {t _ {k} + n } = x _ {n} $, is given. Usually $ n $ is small, $ n = 3, 4, 5 $. The following are often used as indicators of $ y _ {k} $: the mean value $ \overline{x}\; = \sum _ {i=1} ^ {n} x _ {i} /n $, the median, the variance estimator $ s ^ {2} = \sum _ {i=1} ^ {n} ( x _ {i} - \overline{x}\; ) ^ {2} /n $, the range, etc. To begin with, two lines are drawn in the control chart: the upper control boundary (UCB) and the lower control boundary (LCB). If the value of $ y _ {k} $ falls outside these limits, then the industrial process must be altered, in order to re-establish stability.
Control charts were introduced by W.A. Shewhart [3]. A number of variants of the control chart are now (1984) being used (see [4], [5]). The existence of different types of control charts is explained by the fact that they are not all equally effective in detecting different discrepancies. Thus, for stepwise changes of the mean values of $ \epsilon _ {t} $, the so-called of accumulated sums control chart may prove to be more effective than the type shown in the figure. An exact estimate of different characteristics of control charts, for example, of the average delay before a certain type of discrepancy appears, is difficult to achieve, and requires a great deal of calculation, which generally means that it can only be done by using a computer.
In cases where the controlled production is broken down into aggregate-sets, methods of statistical acceptance control are widely used.
References
| [1] | H.F. Dodge, "A sampling inspection plan for continuous production" Ann. Math. Stat. , 14 (1943) pp. 264–279 |
| [2] | Yu.K. Belyaev, "Probabilistic methods of sample control" , Moscow (1975) (In Russian) |
| [3] | W.A. Shewhart, "Economic control of quality of manufactured products" , New York (1931) |
| [4] | E. Shindovskii, O. Shurtz, "Statische Methoden der Kwalitätssteuerung" , Moscow (1976) (In Russian; translated from German) |
| [5] | N. Johnson, F. Leone, "Statistics and experimental design in engineering and the physical sciences" , 1 , Wiley (1964) |
Statistical quality control. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Statistical_quality_control&oldid=54974