Spherical trigonometry
The mathematical discipline that studies the interdependence of the sides and angles of spherical triangles (see Spherical geometry). Let $ A, B, C $
be the angles and let $ a, b, c $
be the opposite sides of a spherical triangle $ ABC $.
The angles and sides of the spherical triangle are related by the following basic formulas of spherical trigonometry:
$$ \tag{1 } \frac{\sin a }{\sin A } = \frac{\sin b }{\sin B } = \frac{\sin c }{\sin C } $$
(the sine theorem);
$$ \tag{2 } \cos a = \cos b \cos c + \sin b \sin c \cos A $$
(the cosine theorem for sides);
$$ \cos A = - \cos B \cos C + \sin B \sin C \cos a $$
(the cosine theorem for angles);
$$ \tag{3 } \sin a \cos B = \cos b \sin c - \sin b \cos c \cos A, $$
$$ \sin A \cos b = \cos B \sin C + \sin B \cos C \cos a $$
(the formulas linking five elements). In these formulas, the sides $ a, b, c $ are measured by the corresponding central angles, and the lengths of these sides are equal respectively to $ aR $, $ bR $, $ cR $, where $ R $ is the radius of the sphere. By changing the notations of the angles and sides according to the circular permutation: $ A \rightarrow B \rightarrow C \rightarrow A $ $ ( a \rightarrow b \rightarrow c \rightarrow a) $ it is possible to write down other formulas of spherical trigonometry, analogous to those shown. The formulas of spherical trigonometry make it possible to determine any three elements of the spherical triangle from the other three.
In order to find a spherical triangle by means of two given sides $ a, b $ and the angle $ C $ between them, and by means of two given angles $ A, B $ and the side $ c $ between them, the following formulas are used (Napier analogues):
$$ \tag{4 } \mathop{\rm tan} A- \frac{B}{2} = \ \frac{\sin \{ ( a- b) / 2 \} }{\sin \{ ( a+ b) / 2 \} } \mathop{\rm cot} \frac{C}{2} ,\ \ $$
$$ \mathop{\rm tan} A+ \frac{B}{2} = \frac{\cos \{ ( a- b) / 2 \} }{ \cos \{ ( a+ b) / 2 \} } \mathop{\rm cot} \frac{C}{2} ; $$
$$ \tag{5 } \mathop{\rm tan} a- \frac{b}{2} = \frac{\sin \{ ( A- B) / 2 \} }{\sin \{ ( A+ B) / 2 \} } \mathop{\rm tan} \frac{c}{2} ,\ \ $$
$$ \mathop{\rm tan} a+ \frac{b}{2} = \frac{\cos \{ ( A- B) / 2 \} }{ \cos \{ ( A+ B) / 2 \} } \mathop{\rm tan} \frac{c}{2} . $$
For right-angled spherical triangles ( $ A = 90 \circ $, $ a $ is the hypotenuse, $ b, c $ are the other two sides), the formulas are simplified, for example:
$$ \tag{1'} \sin b = \sin a \sin B $$
(the sine theorem);
$$ \tag{2'} \cos a = \cos b \cos c $$
(Pythagoras' spherical theorem);
$$ \tag{3'} \sin a \cos B = \cos b \sin c. $$
In solving problems, the following Delambre formulas, which link all six elements of a spherical triangle, are useful:
$$ \sin \frac{a}{2} \cos B- \frac{C}{2} = \sin \frac{A}{2} \sin b+ \frac{c}{2} , $$
$$ \sin \frac{a}{2} \sin B- \frac{C}{2} = \cos \frac{A}{2} \sin b- \frac{c}{2} , $$
$$ \cos \frac{a}{2} \cos B+ \frac{C}{2} = \sin \frac{A}{2} \cos b+ \frac{c}{2} , $$
$$ \cos \frac{a}{2} \sin B+ \frac{C}{2} = \cos \frac{A}{2} \cos b- \frac{c}{2} ; $$
$$ \sin \frac{A}{2} = \sqrt { \frac{\sin ( s- b) \sin ( s- c) }{\sin b \sin c } } , $$
$$ \cos \frac{A}{2} = \sqrt { \frac{\sin s \sin ( s- a) }{\sin b \sin c } } ,\ s = a+ b+ \frac{c}{2} ; $$
$$ \sin \frac{a}{2} = \sqrt { \frac{- \cos S \cos ( S- A) }{\sin B \sin C } } , $$
$$ \cos \frac{a}{2} = \sqrt { \frac{\cos ( S- B) \cos ( S- C) }{\sin B \sin C } } ,\ S = A+ B+ \frac{C}{2} . $$
For references, see Spherical geometry.
Comments
The "analogue" in "Napier analogues" is an old-fashioned word for "proportion" .
From a relation between the elements of a spherical triangle $ ABC $ with sides $ a, b, c $, a second relation can be derived by replacing every element by its supplement and at the same time replacing small letters by the corresponding capitals. An example:
$$ \sin a \cos B = \cos b \sin c - \sin b \cos c \cos A $$
yields
$$ \sin ( 180- A) \cos ( 180- b) = $$
$$ = \ \cos ( 180- B) \sin ( 180- C) + $$
$$ - \sin ( 180- B) \cos ( 180- C) \cos ( 180- a) , $$
i.e.
$$ \sin A \cos b = \cos B \sin C + \sin B \cos C \cos a . $$
Delambre's formulas are also called Gauss' formulas (or Gauss analogues).
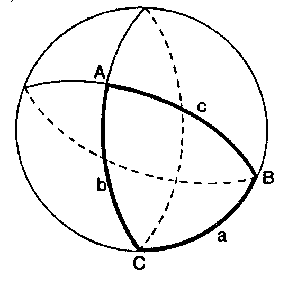
Figure: s086730a
References
| [a1] | H. Flanders, J. Price, "Trigonometry" , Acad. Press (1975) |
| [a2] | G. Hessenberg, H. Kneser, "Ebene und Sphaerische Trigonometrie" , de Gruyter (1957) |
| [a3] | W.A. Granville, P.F. Smith, J.S. Mikesh, "Spherical trigonometry" , Ginn (1943) |
| [a4] | W. Lietzmann, "Elementare Kugelgeometrie" , Vandenhoeck & Ruprecht (1949) |
| [a5] | M. Berger, "Geometry" , II , Springer (1989) |
| [a6] | B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian) |
| [a7] | J.D.H. Donnay, "Spherical trigonometry after the Cesàro method" (1945) |
Spherical trigonometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spherical_trigonometry&oldid=48779