Spectral geometry of Riemannian submersions

Let $\pi : Z \rightarrow Y$ be a Riemannian submersion. Let $D _ { Y }$ and $D _ { Z }$ be operators of Laplace type (cf. also Laplace operator) on $Y$ and $Z$ on bundles $V _ { Y }$ and $V _ { Z }$. Let $E ( \lambda , D _ { Y } )$ and $E ( \lambda , D _ { \operatorname {Z} } )$ be the corresponding eigenspaces. Assume given a pull-back 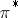from $V _ { Y }$ to $V _ { Z }$. One wants to have examples where there exists

\begin{equation} \tag{a1} 0 \neq \phi \in E ( \lambda , D _ { Y } ) \text { with } \pi ^ { * } \phi \in E ( \mu , D _ { Z } ). \end{equation}

One also wants to know when

\begin{equation} \tag{a2} \pi ^ { * } E ( \lambda , D _ { Y } ) \subset E ( \mu ( \lambda ) , D _ { Z } ). \end{equation}

Let $\pi : S ^ { 3 } \rightarrow S ^ { 2 }$ and let $\nu_2$ be the volume element on $S ^ { 2 }$. Let $\Delta ^ { p }$ be the Laplace–Beltrami operator (cf. also Laplace–Beltrami equation). Y. Muto [a8], [a7] observed that

\begin{equation*} 0 \neq \nu _ { 2 } \in E ( 0 , \Delta _ { S^2 } ^ { 2 } ) \end{equation*}

\begin{equation*} \pi ^ { * } \nu _ { 2 } \in E ( \mu , \Delta _ { S^3 } ^ { 2 } ) \end{equation*}

for $\mu \neq 0$; he also gave other examples involving principal fibre bundles.

S.I. Goldberg and T. Ishihara [a2] and B. Watson [a9] studied this question and determined some conditions to ensure that (a2) holds with $\mu ( \lambda ) = \lambda$ for all $\lambda$; this work was later extended in [a5] for the real Laplacian and in [a3] for the complex Laplacian. If (a1) holds for a single eigenvalue, then $\lambda \leq \mu$ (eigenvalues cannot decrease). See also [a1] for a discussion of the case in which the fibres are totally geodesic. See [a6] for related results in the spin setting. For a survey of the field, see [a4].

References

[a1]	L. Berard Bergery, J.P. Bourguignon, "Laplacians and Riemannian submersions with totally geodesic fibers" Illinois J. Math. , 26 (1982) pp. 181–200
[a2]	S.I. Goldberg, T. Ishihara, "Riemannian submersions commuting with the Laplacian" J. Diff. Geom. , 13 (1978) pp. 139–144
[a3]	P. Gilkey, J. Leahy, J.H. Park, "The eigenforms of the complex Laplacian for a holomorphic Hermitian submersion" Nagoya Math. J. (to appear)
[a4]	P. Gilkey, J. Leahy, J.H. Park, "Spinors, spectral geometry, and Riemannian submersions" , Lecture Notes , 40 , Research Inst. Math., Global Analysis Research Center, Seoul Nat. Univ. (1998)
[a5]	P. Gilkey, J.H. Park, "Riemannian submersions which preserve the eigenforms of the Laplacian" Illinois J. Math. , 40 (1996) pp. 194–201
[a6]	A. Moroianu, "Opérateur de Dirac et Submersions Riemanniennes" Thesis École Polytechn. Palaiseau (1996)
[a7]	Y. Muto, "Riemannian submersion and the Laplace–Beltrami operator" Kodai Math. J. , 1 (1978) pp. 329–338
[a8]	Y. Muto, "Some eigenforms of the Laplace–Beltrami operators in a Riemannian submersion" J. Korean Math. Soc. , 15 (1978) pp. 39–57
[a9]	B. Watson, "Manifold maps commuting with the Laplacian" J. Diff. Geom. , 8 (1973) pp. 85–94
[a10]	Y. Muto, "$\delta$ commuting mappings and Betti numbers" Tôhoku Math. J. , 27 (1975) pp. 135–152