Solvable flow
A flow on a solv manifold $ M = G/H $
determined by the action on $ M $
of some one-parameter subgroup $ g _ {t} $
of the solvable Lie group $ G $:
If $ M $
consists of the cosets $ gH $,
then under the action of the solvable flow such a coset goes to the coset $ g _ {t} gH $
at time $ t $.
A particular case of a solvable flow is a nil-flow; in the general case the properties of a solvable flow can be considerably more diverse.
References
| [1] | L. Auslander, L. Green, F. Hahn, "Flows on homogeneous spaces" , Princeton Univ. Press (1963) |
| [2] | A.M. Stepin, "Flows on solvmanifolds" Uspekhi Mat. Nauk , 24 : 5 (1969) pp. 241 (In Russian) |
| [3] | L. Auslander, "An exposition of the structure of solvmanifolds. Part II: 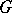 -induced flows" Bull. Amer. Math. Soc. , 79 : 2 (1973) pp. 262–285 -induced flows" Bull. Amer. Math. Soc. , 79 : 2 (1973) pp. 262–285 |
| [4] | A.V. Safonov, "Spectral type of 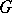 -induced ergodic flows" Functional Anal. Appl. , 14 : 4 (1980) pp. 315–317 Funkts. Anal. i Prilozhen. , 14 : 4 (1980) pp. 81–82 -induced ergodic flows" Functional Anal. Appl. , 14 : 4 (1980) pp. 315–317 Funkts. Anal. i Prilozhen. , 14 : 4 (1980) pp. 81–82 |
| [5] | L. Auslander, L. Green, "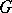 -induced flows and solvmanifolds" Amer. J. Math. , 88 (1966) pp. 43–60 -induced flows and solvmanifolds" Amer. J. Math. , 88 (1966) pp. 43–60 |
Comments
In many cases dynamical properties of the flow, such as ergodicity, can be deduced from algebraic properties of $ G $ and $ H $. The Kronecker theorem implies ergodicity for the case $ G = \mathbf R ^ {n} $, $ H = \mathbf Z ^ {n} $, the integer lattice, and the flow (written additively) given by $ g _ {t} ( x + \mathbf Z ^ {n} ) = x + t a + \mathbf Z ^ {n} $, where $ x + \mathbf Z ^ {n} $ is a coset of $ \mathbf R ^ {n} / \mathbf Z ^ {n} $ and $ a \in \mathbf R ^ {n} $ is a fixed vector whose components are linearly independent over the rational numbers. When $ G= \mathop{\rm SL} ( 2, \mathbf R ) $ and $ H $ is a discrete subgroup, certain one-parameter subgroups of $ G $ correspond to geodesic and horocycle flow (cf. Geodesic flow; Horocycle flow) on unit tangent bundles of surfaces of constant negative curvature (cf. Constant curvature, space of).
References
| [a1] | J. Brezin, C.C. Moore, "Flows on homogeneous spaces" Amer. J. Math. , 103 (1981) pp. 571–613 |
Solvable flow. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Solvable_flow&oldid=48748