Smolyak algorithm

Boolean method, discrete blending method, hyperbolic cross points method, sparse grid method, fully symmetric quadrature formulas

Many high-dimensional problems are difficult to solve, cf. also Optimization of computational algorithms; Information-based complexity; Curse of dimension. High-dimensional linear tensor product problems can be solved efficiently by the Smolyak algorithm, which provides a general principle to construct good approximations for the $d$-dimensional case from approximations for the univariate case. The Smolyak algorithm is often optimal or almost optimal if approximations for the univariate case are properly chosen.

The original paper of S.A. Smolyak was published in 1963 [a6]. There exist many variants of the basic algorithm for specific problems, see [a1], [a2], [a3], [a4], [a5], [a6], [a7], [a8], [a9], [a10]. For a thorough analysis with explicit error bounds see [a8], for major modifications see [a9]. The basic idea is here explained using the examples of multivariate integration and approximation. Assume one wishes to approximate, for smooth functions $f \in C ^ { k } ( [ 0,1 ] ^ { d } )$,

\begin{equation*} I _ { d } ( f ) = \int _ { [ 0,1 ] ^ { d } } f ( x ) d x\; \text { or }\; I _ { d } ( f ) = f, \end{equation*}

using finitely many function values of $f$. Multivariate integration (the first $I _ { d }$) is needed in many areas even for very large $d$, and often a Monte-Carlo method or number-theoretic method (based on low-discrepancy sequences, see Discrepancy) are used. Multivariate approximation (the second $I _ { d }$) is often part of the solution of operator equations using the Galerkin method, see [a2], [a4], [a10].

For $d = 1$, much is known about good quadrature or interpolation formulas

\begin{equation*} U ^ { i } ( f ) = \sum _ { j = 1 } ^ { m _ { i } } f ( x _ { j } ^ { i } ) \cdot a _ { j } ^ { i }. \end{equation*}

(Cf. also Quadrature formula; Interpolation formula.) Here, $a ^ { i }_{j} \in \mathbf{R}$ for quadrature formulas and $a _ { j } ^ { i } \in C ( [ 0,1 ] )$ for approximation formulas. It is assumed that a sequence of such $U ^ { i }$ with $m _ { i } = 2 ^ { i - 1 }$ is given. For $C ^ { k }$-functions the optimal order is

\begin{equation} \tag{a1} e ( U ^ { i } , f ) \leq C _ { 1 }. m _ { i } ^ { - k }. \| f \| _ { k }, \end{equation}

where $\| . \| _ { k }$ is a norm on $C ^ { k } ( [ 0,1 ] )$, as in (a2). The error $e ( U ^ { i } , f )$ is defined by $| I _ { 1 } ( f ) - U ^ { i } ( f ) |$ and $\| I _ { 1 } ( f ) - U ^ { i } ( f ) \| _ { 0 }$, respectively. In the multivariate case $d > 1$, one first defines tensor product formulas

\begin{equation*} ( U ^ { i _ { 1 } } \bigotimes \ldots \bigotimes U ^ { i _ { d } } ) ( f ) = \end{equation*}

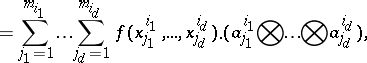which serve as building blocks for the Smolyak algorithm. Then the Smolyak algorithm can be written as

\begin{equation*} A ( q , d ) = \end{equation*}

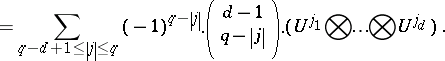To compute $A ( q , d ) ( f )$, one only needs to know function values at the "sparse grid"

\begin{equation*} H ( q , d ) = \cup _ { q - d + 1 \leq | j | \leq q } ( X ^ { j _ { 1 } } \times \ldots \times X ^ { j _ { d } } ), \end{equation*}

where $X ^ { i } = \{ x _ { 1 } ^ { i } , \ldots , x ^ { i _{m _ { i }} } \} \subset [ 0,1 ]$ denotes the set of points used by $U ^ { i }$. For the tensor product norm

\begin{equation} \tag{a2} \| f \| _ { k } = \operatorname { max } \{ \| D ^ { \alpha } f \| _ { L _ { \infty } } : \alpha \in \mathbf{N} _ { 0 } ^ { d } , \alpha _ { i } \leq k \}, \end{equation}

the error bound

\begin{equation} \tag{a3} e ( A ( q , d ) , f ) \leq C _ { d }. n ^ { - k } .( \operatorname { log } n ) ^ { ( d - 1 ) . ( k + 1 ) }. \| f \| _ { k } \end{equation}

follows from (a1), where $n$ is the number of points in $H ( q , d )$. This is the basic result of [a6]; see [a8], [a9] for much more explicit error bounds. The error bound (a3) should be compared with the optimal order $n ^ { - k / d }$ of tensor product formulas.

References

[a1]	F.-J. Delvos, W. Schempp, "Boolean methods in interpolation and approximation" , Pitman Res. Notes Math. , 230 , Longman (1989)
[a2]	K. Frank, S. Heinrich, S. Pereverzev, "Information complexity of multivariate Fredholm integral equations in Sobolev classes" J. Complexity , 12 (1996) pp. 17–34
[a3]	A.C. Genz, "Fully symmetric interpolatory rules for multiple integrals" SIAM J. Numer. Anal. , 23 (1986) pp. 1273–1283
[a4]	M. Griebel, M. Schneider, Ch. Zenger, "A combination technique for the solution of sparse grid problems" R. Beauwens (ed.) P. de Groen (ed.) , Iterative Methods in Linear Algebra , Elsevier& North-Holland (1992) pp. 263–281
[a5]	E. Novak, K. Ritter, "High dimensional integration of smooth functions over cubes" Numer. Math. , 75 (1996) pp. 79–97
[a6]	S.A. Smolyak, "Quadrature and interpolation formulas for tensor products of certain classes of functions" Soviet Math. Dokl. , 4 (1963) pp. 240–243
[a7]	V.N. Temlyakov, "Approximation of periodic functions" , Nova Science (1994)
[a8]	G.W. Wasilkowski, H. Woźniakowski, "Explicit cost bounds of algorithms for multivariate tensor product problems" J. Complexity , 11 (1995) pp. 1–56
[a9]	G.W. Wasilkowski, H. Woźniakowski, "Weighted tensor-product algorithms for linear multivariate problems" Preprint (1998)
[a10]	A.G. Werschulz, "The complexity of the Poisson problem for spaces of bounded mixed derivatives" J. Renegar (ed.) M. Shub (ed.) S. Smale (ed.) , The Mathematics of Numerical Analysis , Lect. Appl. Math. , 32 , Amer. Math. Soc. (1996) pp. 895–914