Semi-regular polyhedra
uniform polyhedra, Archimedean solids
A uniform polyhedron is a polyhedron all faces of which are regular polygons, while any vertex is related to all the other vertices by symmetry operations. Thus, the convex uniform polyhedra consist of the five Platonic solids along with those given in the Table, where $ V $ is the number of vertices, $ E $ the number of edges, $ F $ the number of faces, $ F _ {k} $ the number of $ n _ {k} $- gonal faces, $ s $ the number of faces meeting at each vertex, namely $ s _ {1} $ $ n _ {1} $- gonal faces, $ s _ {2} $ $ n _ {2} $- gonal faces, etc.
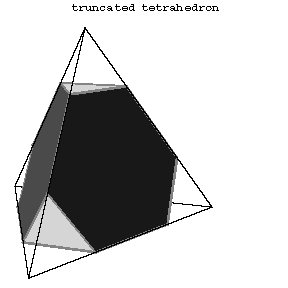
Figure: s084300a
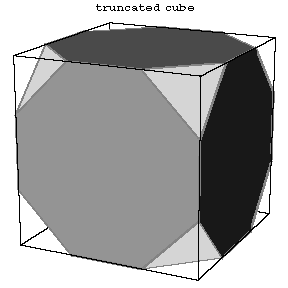
Figure: s084300b

Figure: s084300c

Figure: s084300d

Figure: s084300e

Figure: s084300f
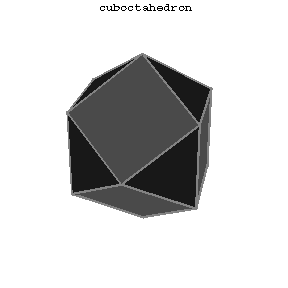
Figure: s084300g
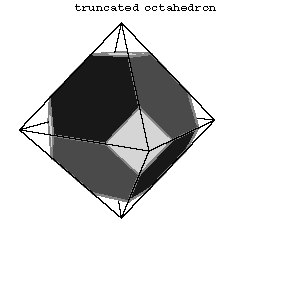
Figure: s084300h
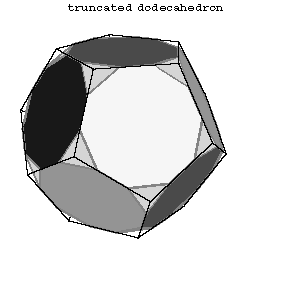
Figure: s084300i

Figure: s084300j

Figure: s084300k

Figure: s084300l
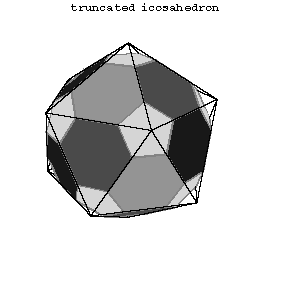
Figure: s084300m

Figure: s084300n

Figure: s084300o

Figure: s084300p
<tbody> </tbody>
|
The first 13 polyhedra in the Table are attributed to Archimedes (Fig. a, Fig. b, Fig. c, 5–14).
In addition to the 13 solids of Archimedes and the convex prisms (Fig.15) and antiprisms (Fig.16), there are non-convex prisms and antiprisms whose bases are "star polygons" , and 53 other non-convex uniform polyhedra.
References
| [1] | P.S. Alexandroff [P.S. Aleksandrov] (ed.) et al. (ed.) , Enzyklopaedie der Elementarmathematik , 4. Geometrie , Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian) |
| [2] | L.A. Lyusternik, "Convex figures and polyhedra" , Moscow (1956) (In Russian) |
| [3] | M. Brückner, "Vielecke und Vielflache. Theorie und Geschichte" , Teubner (1900) |
| [4] | M. Wenninger, "Polyhedron models" , Cambridge Univ. Press (1971) |
Comments
The individual names of the "Archimedean polyhedra" were coined by J. Kepler [a6], pp. 10–11, who referred to "fourteen Archimedean solids" (Archimedeis quattuordecim). The extra one (Fig. d) is the pseudo-rhombicubocahedron, which is not strictly "uniform" because, although all its polyhedral angles are congruent, they are of two different types from the standpoint of symmetry.
References
| [a1] | H.S.M. Coxeter, "Regular and semi-regular polytopes I" Math. Z. , 46 (1940) pp. 380–407 |
| [a2] | H.S.M. Coxeter, "Regular and semi-regular polytopes II" Math. Z. , 188 (1985) pp. 559–591 |
| [a3] | H.S.M. Coxeter, "Regular and semi-regular polytopes III" Math. Z. , 200 (1988) pp. 3–45 |
| [a4] | S.A. Robertson, "Polytopes and symmetry" , Cambridge Univ. Press (1984) |
| [a5] | L. Fejes Toth, "Lagerungen in der Ebene, auf der Kugel und im Raum" , Springer (1972) |
| [a6] | J. Kepler, "Strena: The six-cornered snowflake" , Oxford Univ. Press (1966) |
| [a7] | H. Senechal (ed.) G. Fleck (ed.) , Shaping space , Birkhäuser (1988) |
| [a8] | W.W.R. Ball, H.S.M. Coxeter, "Mathematical recreations and essays" , Dover, reprint (1987) pp. Chapt. 5 |
Semi-regular polyhedra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-regular_polyhedra&oldid=48666