Steiner system
A pair  , where
, where  is a finite set of
is a finite set of  elements and
elements and  is a set of
is a set of  -subsets in
-subsets in  (called blocks) such that every
(called blocks) such that every  -subset from
-subset from  is contained in exactly one block of
is contained in exactly one block of 
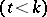 . The number
. The number  is called the order of the Steiner system
is called the order of the Steiner system 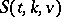 . A Steiner system is a particular case of a block design and of a tactical configuration. A Steiner system for
. A Steiner system is a particular case of a block design and of a tactical configuration. A Steiner system for  is a balanced incomplete block design (BIBD), and for
is a balanced incomplete block design (BIBD), and for 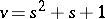 ,
, 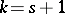 it is a finite projective plane. A necessary condition for the existence of a Steiner system
it is a finite projective plane. A necessary condition for the existence of a Steiner system  is that the number
is that the number
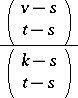 |
is an integer for all  satisfying
satisfying 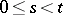 . The sufficiency of this condition was proved for
. The sufficiency of this condition was proved for 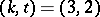 ,
, 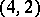 ,
, 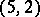 ,
, 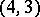 (see [3], [4]).
(see [3], [4]).
In 1844 W. Woolhouse stated the existence problem for Steiner systems, and P. Kirkman solved it in 1847 for 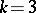 (Steiner triple systems). In 1853 J. Steiner examined the case of
(Steiner triple systems). In 1853 J. Steiner examined the case of 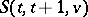 .
.
Problems usually considered for Steiner systems are: 1) the determination of the maximum number of mutually non-isomorphic Steiner systems of a given order  ; 2) the existence of Steiner systems with a given group of automorphisms; 3) the imbedding of partial Steiner systems (not containing some
; 2) the existence of Steiner systems with a given group of automorphisms; 3) the imbedding of partial Steiner systems (not containing some 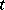 -subsets of
-subsets of 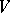 ) in a finite Steiner system; 4) the existence of resolvable Steiner systems (with
) in a finite Steiner system; 4) the existence of resolvable Steiner systems (with 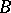 representable as a union of partitions of
representable as a union of partitions of 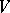 ); 5) the maximal packing (minimal covering) of a complete set of
); 5) the maximal packing (minimal covering) of a complete set of  -subsets of
-subsets of  by disjoint
by disjoint 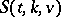 (using Steiner systems).
(using Steiner systems).
The majority of results on Steiner systems are obtained for small values of 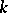 and
and 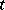 (see [2]–[4]).
(see [2]–[4]).
References
| [1] | J. Steiner, "Combinatorische Aufgaben" J. Reine Angew. Math. , 45 (1853) pp. 181–182 |
| [2] | M. Hall, "Combinatorial theory" , Wiley (1986) |
| [3] | C.C. Lindner, A. Rosa, "Steiner quadruple systems. A survey" Discrete Math. , 22 (1978) pp. 147–181 |
| [4] | H. Hanani, "Balanced incomplete block designs and related designs" Discrete Math. , 11 (1975) pp. 255–369 |
Comments
The name "Steiner system" is somewhat inappropriate, since the systems studied by Steiner in [1] are not Steiner systems 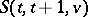 for
for 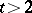 .
.
There is a rapidly growing literature on Steiner systems and related types of incidence structures, comprising thousands of papers. In what follows, only very few outstanding original papers are quoted; the reader is instead referred to the textbooks [2], [a1]–[a2], the collections of papers [a3]–[a5] and the surveys [a6]–[a8] for a detailed discussion and complete references. Regarding the existence of small systems, the reader should consult the tables [a9]–[a10].
The main problems usually studied are as follows.
Existence.
The only pairs 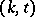 for which the existence problem is completely settled are still those listed in the original article above. For
for which the existence problem is completely settled are still those listed in the original article above. For  a very strong asymptotic existence result is due to R.M. Wilson [a11]–[a13]: For any fixed
a very strong asymptotic existence result is due to R.M. Wilson [a11]–[a13]: For any fixed  , the necessary conditions
, the necessary conditions 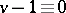
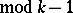 and
and 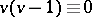
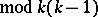 are sufficient for all but finitely many values of
are sufficient for all but finitely many values of  . Unfortunately, the bounds on
. Unfortunately, the bounds on  extractable from Wilson's work are exceedingly large. Progress has been made for some small values of
extractable from Wilson's work are exceedingly large. Progress has been made for some small values of  ; e.g., for
; e.g., for 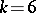 there are only 89 values of
there are only 89 values of  left for which the existence of an
left for which the existence of an 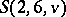 is undecided, the largest of which is
is undecided, the largest of which is 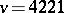 . Similar results hold for
. Similar results hold for 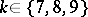 . Considerably less is known for
. Considerably less is known for 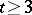 . The outstanding problem of the existence of non-trivial Steiner systems with
. The outstanding problem of the existence of non-trivial Steiner systems with 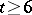 is still open. For
is still open. For 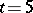 , existence is known only for the seven pairs
, existence is known only for the seven pairs 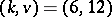 ,
, 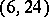 ,
, 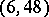 ,
, 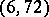 ,
, 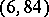 ,
, 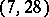 , and
, and 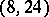 .
.
Enumeration.
Once existence is settled, one is interested in the number 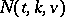 of isomorphism classes of Steiner systems
of isomorphism classes of Steiner systems 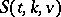 . The function
. The function  grows very rapidly with
grows very rapidly with  (for fixed
(for fixed 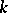 ); e.g.,
); e.g., 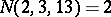 ,
, 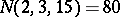 , but
, but 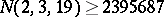 . Wilson [a11]–[a13] proved
. Wilson [a11]–[a13] proved 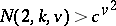 for all admissible
for all admissible  which are sufficiently large (where
which are sufficiently large (where 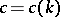 is a constant depending on
is a constant depending on 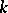 ). For
). For 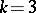 , one has
, one has
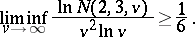 |
The only known similar result for 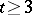 concerns
concerns 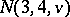 . For some small parameter triples, a complete enumeration is possible. E.g., the projective and affine planes are unique up to order 8, and so are the Witt designs
. For some small parameter triples, a complete enumeration is possible. E.g., the projective and affine planes are unique up to order 8, and so are the Witt designs 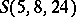 and
and 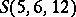 [a14].
[a14].
Automorphism groups.
Much effort is spent in constructing Steiner systems with "nice" (usually this means large, at least point-transitive) automorphism groups. It appears that most Steiner systems are rigid (i.e., have no non-trivial automorphism), but this has only been demonstrated for  (where it is known that the proportion of rigid Steiner triple systems
(where it is known that the proportion of rigid Steiner triple systems  among all Steiner triple systems
among all Steiner triple systems  approaches 1 as
approaches 1 as 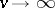 ). The particularly interesting existence problem for cyclic Steiner systems (those with a point-transitive cyclic group of automorphisms) has also been settled completely only for
). The particularly interesting existence problem for cyclic Steiner systems (those with a point-transitive cyclic group of automorphisms) has also been settled completely only for 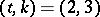 ; the case
; the case 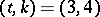 is at present studied extensively.
is at present studied extensively.
Characterization and classification.
In view of the results on 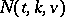 mentioned above, the complete classification of all
mentioned above, the complete classification of all 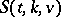 is only feasible for small values of the parameters. One therefore is interested in characterizing the "classical" series of examples (in particular, the Steiner systems
is only feasible for small values of the parameters. One therefore is interested in characterizing the "classical" series of examples (in particular, the Steiner systems 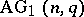 and
and  formed by the points and lines in the
formed by the points and lines in the  -dimensional affine, respectively projective, space over
-dimensional affine, respectively projective, space over 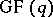 and the Hermitian unitals formed by the absolute points and the non-absolute lines of a unitary polarity of
and the Hermitian unitals formed by the absolute points and the non-absolute lines of a unitary polarity of 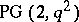 ) and in classifying Steiner systems with interesting automorphism groups. E.g., all systems
) and in classifying Steiner systems with interesting automorphism groups. E.g., all systems 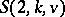 with a group which is
with a group which is  -homogeneous on points have been classified; except for the three classical series just mentioned, there are only two further series and a few sporadic examples. At present one works on the classification of systems
-homogeneous on points have been classified; except for the three classical series just mentioned, there are only two further series and a few sporadic examples. At present one works on the classification of systems 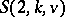 with a flag-transitive or a point-primitive group.
with a flag-transitive or a point-primitive group.
Resolvable Steiner systems.
Here 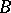 is a union of parallel classes (i.e., partitions of the point set
is a union of parallel classes (i.e., partitions of the point set 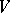 ). A resolvable
). A resolvable 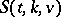 is usually denoted by
is usually denoted by 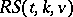 and also called a Kirkman system (since the seminal case of an
and also called a Kirkman system (since the seminal case of an 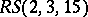 is equivalent to a solution of Kirkman's famous schoolgirl problem posed in 1850). One clearly has the further necessary condition
is equivalent to a solution of Kirkman's famous schoolgirl problem posed in 1850). One clearly has the further necessary condition 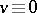
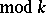 for the existence of an
for the existence of an 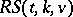 . For
. For 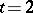 , the necessary condition
, the necessary condition 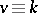
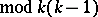 is known to be sufficient for
is known to be sufficient for  and
and 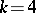 ; it is also asymptotically sufficient for any fixed
; it is also asymptotically sufficient for any fixed 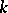 . The cases
. The cases 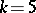 and
and 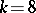 are almost settled (with about 100 undecided values of
are almost settled (with about 100 undecided values of  in either case). Much less is known for
in either case). Much less is known for 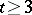 ; only the case
; only the case 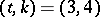 is almost settled.
is almost settled.
Subsystems.
Another problem of interest is the existence of an 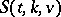 with a subsystem
with a subsystem 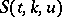 . Up till now (1990) this has only been considered for
. Up till now (1990) this has only been considered for 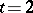 . Here one obtains the additional necessary condition
. Here one obtains the additional necessary condition 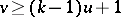 , which is known to be sufficient for
, which is known to be sufficient for 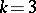 and
and 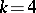 . Similarly, an
. Similarly, an 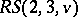 with a sub-
with a sub-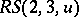 exists if and only if
exists if and only if 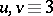
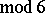 and
and 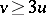 .
.
Imbeddings.
One question concerns the possibility of imbedding a "partial" 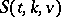 in some
in some 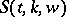 . E.g., a partial
. E.g., a partial 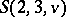 can be imbedded in an
can be imbedded in an 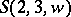 for all values of
for all values of 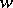 with
with 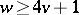 and
and 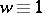 or
or 
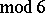 . Another question which has been studied in many special instances concerns imbeddings of partial
. Another question which has been studied in many special instances concerns imbeddings of partial 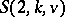 's in finite projective planes. Here the outstanding problem is the conjecture that any partial
's in finite projective planes. Here the outstanding problem is the conjecture that any partial  can be imbedded in a finite projective plane (possibly even in a Desarguesian plane
can be imbedded in a finite projective plane (possibly even in a Desarguesian plane 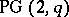 ).
).
Large sets of Steiner systems and packings.
A large set is a partition of the set of all 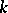 -subsets of a
-subsets of a  -set into Steiner systems
-set into Steiner systems 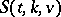 . The outstanding result here is the existence of a large set of
. The outstanding result here is the existence of a large set of 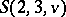 for all
for all  or
or 
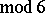 (with 6 possible exceptions) proved by Lu Jia-Xi in a series of papers [a15]. One also knows the existence of a large set of
(with 6 possible exceptions) proved by Lu Jia-Xi in a series of papers [a15]. One also knows the existence of a large set of  's. More generally, one is interested in (bounds on) the maximum number
's. More generally, one is interested in (bounds on) the maximum number 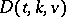 of pairwise disjoint
of pairwise disjoint 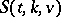 's (i.e. packings of
's (i.e. packings of 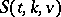 's).
's).
Generalizations.
Steiner systems have been generalized in many ways, and problems analogous to the ones discussed here are studied for these generalizations. The most obvious generalization is that to  's, where one requires that any
's, where one requires that any 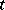 -set of points is contained in exactly
-set of points is contained in exactly 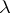 common blocks. An
common blocks. An 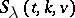 is called simple if there are no two blocks which are incident with the same set of points. L. Teirlinck [a16] proved that there exist non-trivial simple
is called simple if there are no two blocks which are incident with the same set of points. L. Teirlinck [a16] proved that there exist non-trivial simple 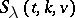 's for every
's for every 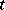 , thus settling an outstanding problem. Another generalization is allowance of different block sizes; this has been mainly studied for the case
, thus settling an outstanding problem. Another generalization is allowance of different block sizes; this has been mainly studied for the case 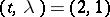 ; the resulting structures are called pairwise balanced designs and are a fundamental tool for the existence theory of Steiner systems with
; the resulting structures are called pairwise balanced designs and are a fundamental tool for the existence theory of Steiner systems with 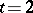 . One also considers packing and covering of all
. One also considers packing and covering of all 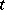 -subsets of a
-subsets of a  -set by
-set by 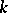 -subsets. Finally, sets of mutually orthogonal Latin squares can be considered as a generalization of affine planes, i.e. of systems
-subsets. Finally, sets of mutually orthogonal Latin squares can be considered as a generalization of affine planes, i.e. of systems 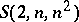 .
.
Connections to other areas.
Finally, the study of Steiner systems and their generalizations is closely connected to several other areas of mathematics, such as geometry, group theory and coding theory. The best-known example is provided by the Witt designs mentioned above, which are essentially equivalent to the Mathieu groups and the Golay codes, see [a1], [a17], [a18]. On the other hand, there are also important applications of combinatorial designs in general, and Steiner systems in particular, e.g. in computer science and cryptography [a19].
References
| [a1] | T. Beth, D. Jungnickel, H. Lenz, "Design theory" , Cambridge Univ. Press (1986) |
| [a2] | D.R. Hughes, F.C. Piper, "Design theory" , Cambridge Univ. Press (1985) |
| [a3] | C.C. Lindner (ed.) A. Rosa (ed.) , Topics on Steiner systems , North-Holland (1980) |
| [a4] | C.J. Colbourn (ed.) R.A. Mathon (ed.) , Combinatorial design theory , North-Holland (1987) |
| [a5] | A. Hartman (ed.) , Combinatorial designs , North-Holland (1989) |
| [a6] | J. Doyen, A. Rosa, "An extended bibliography and survey of Steiner systems" Congressus Numerantium , 20 (1978) pp. 297–361 |
| [a7] | J. Doyen, A. Rosa, "An extended bibliography of Steiner systems" Ann. Discr. Math. , 7 (1980) pp. 317–349 |
| [a8] | D. Jungnickel, "Design theory: an update" Ars Comb. , 28 (1989) pp. 129–199 |
| [a9] | R.A. Mathon, A. Rosa, "Tables of parameters of BIBD's with 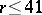 including existence, enumeration and resolvability results: an update" Ars Comb. (To appear) including existence, enumeration and resolvability results: an update" Ars Comb. (To appear) |
| [a10] | Y.M. Chee, C.J. Colbourn, D.L. Kreher, "Simple 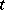 -designs with -designs with 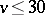 " Ars Comb. , 29 (1990) pp. 193–258 " Ars Comb. , 29 (1990) pp. 193–258 |
| [a11] | R.M. Wilson, "An existence theory for pairwise balanced designs I" J. Comb. Th. (A) , 13 (1972) pp. 220–245 |
| [a12] | R.M. Wilson, "An existence theory for pairwise balanced designs II" J. Comb. Th. (A) , 13 (1972) pp. 246–273 |
| [a13] | R.M. Wilson, "An existence theory for pairwise balanced designs III" J. Comb. Th. (A) , 18 (1975) pp. 71–79 |
| [a14] | E. Witt, "Über Steinersche Systeme" Abh. Math. Sem. Hamburg , 12 (1938) pp. 265–275 |
| [a15] | Jia-Xi Lu, "On large sets of disjoint Steiner triple systems, VI" J. Comb. Th. (A) , 37 (1984) pp. 189–192 |
| [a16] | L. Teirlinck, "Non-trivial 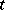 -designs without repeated blocks exist for all -designs without repeated blocks exist for all 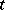 " Discr. Math. , 65 (1987) pp. 301–311 " Discr. Math. , 65 (1987) pp. 301–311 |
| [a17] | F.J. MacWilliams, N.J.A. Sloane, "The theory of error-correcting codes" , I-II , North-Holland (1978) |
| [a18] | H. Lüneburg, "Transitive Erweiterungen endlicher Permutationsgruppen" , Lect. notes in math. , 84 , Springer (1969) |
| [a19] | C.J. Colbourn, P.C. van Oorschot, "Applications of combinatorial designs in computer science" ACM Comp. Surveys , 21 (1989) pp. 223–250 |
STS. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=STS&oldid=45393