Riesz theorem
Riesz's uniqueness theorem for bounded analytic functions: If $ f( z) $
is a bounded regular analytic function in the unit disc $ D = \{ {z \in \mathbf C } : {| z | < 1 } \} $
having zero radial boundary values (cf. Radial boundary value) on a subset $ E $
of the circle $ \Gamma = \{ {z } : {| z | = 1 } \} $
of positive measure, $ \mathop{\rm mes} E > 0 $,
then $ f( z) \equiv 0 $.
The theorem was formulated and proved by the brothers F. Riesz and M. Riesz in 1916 (see ).
This theorem is one of the first boundary value theorems on the uniqueness of analytic functions. Independently of the brothers Riesz, general boundary value theorems on uniqueness were obtained by N.N. Luzin and I.I. Privalov (see , , and Luzin–Privalov theorems).
Riesz's theorem on the Cauchy integral: If $ f( z) $ is a Cauchy integral,
$$ f( z) = \frac{1}{2 \pi i } \int\limits _ \Gamma \frac{f( \zeta ) d \zeta }{\zeta - z } , $$
in the unit disc $ D $ and its boundary values $ f( \zeta ) = f( e ^ {i \theta } ) $ form a function of bounded variation on $ \Gamma $, then $ f( \zeta ) $ is an absolutely-continuous function on $ \Gamma $( see [1]).
This theorem can be generalized to Cauchy integrals along any rectifiable contour $ \Gamma $( see [3]).
References
| [1] | F. Riesz, M. Riesz, "Ueber die Randwerte einer analytischen Funktion" G. Mittag-Leffler (ed.) , 4th Congress Math. Scand. , Almqvist & Wiksells (1920) pp. 27–44 |
| [2] | I.I. Privalov, "The Cauchy integral" , Saratov (1918) (In Russian) |
| [3] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
Comments
The F. and M. Riesz theorem is usually stated as follows: If $ \mu $ is a complex Borel measure on the unit circle $ \Gamma $ and if
$$ \int\limits _ \Gamma e ^ {- {i n t } } d \mu ( t) = 0,\ \ n = - 1, - 2 \dots $$
then $ \mu $ is absolutely continuous with respect to Lebesgue measure, and Lebesgue measure is absolutely continuous with respect to $ \mu $.
This theorem has been generalized both in the setting of function algebras and in the setting of harmonic analysis on groups. As an example of the first there is the following theorem.
Let $ \Phi $ be a continuous homomorphism of the function algebra $ A $ on $ X $, suppose $ \Phi $ has only one representing measure $ \mu $ on $ X $, let $ \nu \in A ^ \perp $, i.e. $ \nu $ annihilates $ A $, and let
$$ \nu = \nu _ \mu + \nu _ {s} $$
be the Lebesgue decomposition of $ \nu $ with respect to $ \mu $. Then $ \nu _ \mu \in A ^ \perp $ and $ \nu _ {s} \in A ^ \perp $.
There is a more general theorem, where the condition that $ \Phi $ has only one representing measure is removed, cf. [a5]. In the other setting one tries to infer from vanishing of part of the spectrum of a measure that it is absolutely continuous with respect to the invariant measure, cf. [a1].
Another theorem due to F. Riesz is the Riesz representation theorem. Let $ X $ be a locally compact Hausdorff space and $ C _ {0} ( X) $ the space of compactly-supported continuous functions on $ X $. Then each bounded linear functional $ \Phi $ on $ C _ {0} ( X) $ has the form
$$ \Phi ( f ) = \int\limits _ { X } f d \mu \ ( f \in C _ {0} ( X)), $$
where $ \mu $ is a complex regular Borel measure on $ X $. Moreover, $ \mu $ is unique.
See e.g., [a6].
References
| [a1] | R.G.M. Brummelhuis, "An F. and M. Riesz theorem for bounded symmetric domains" Ann. Inst. Fourier , 37 (1987) pp. 139–150 |
| [a2] | P.L. Duren, "Theory of 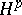 spaces" , Acad. Press (1970) spaces" , Acad. Press (1970) |
| [a3] | J.-B. Garnett, "Bounded analytic functions" , Acad. Press (1981) |
| [a4] | P. Koosis, "Introduction to 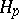 -spaces. With an appendix on Wolff's proof of the corona theorem" , Cambridge Univ. Press (1980) -spaces. With an appendix on Wolff's proof of the corona theorem" , Cambridge Univ. Press (1980) |
| [a5] | W. Rudin, "Function theory in the unit ball in 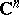 " , Springer (1980) " , Springer (1980) |
| [a6] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1966) pp. 98 |
Riesz theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riesz_theorem&oldid=48569