Representation of an associative algebra
$ A $ of dimension $ n $
A homomorphism of the algebra $ A $ over a field $ k $ into the algebra of matrices $ M _ {n} ( k) $, i.e. a mapping assigning to each $ a \in A $ a square matrix $ T ( a) $ of order $ n $ such that
$$ \tag{* } T ( \lambda a + \mu b) = \lambda T ( a) + \mu T ( b) \ \ \textrm{ and } \ \ T ( ab) = T ( a) T ( b), $$
where $ a, b \in A $, $ \lambda , \mu \in k $. It is usually also required that the unit in $ A $ corresponds to the identity matrix; sometimes $ A $ is also required to be finite-dimensional.
Every indecomposable representation of a finite-dimensional semi-simple algebra is equivalent to a direct summand of the regular representation. Hence, every finite-dimensional semi-simple algebra is an algebra of finite (representation) type, i.e. has a finite number of non-isomorphic indecomposable representations. Non-semi-simple algebras can be both of finite and of infinite representation type (e.g. such is the algebra $ A = \{ {1, r, s } : {r ^ {2} = s ^ {2} = rs = sr = 0 } \} $). Algebras of infinite type are further divided into algebras of wild type, whose classification problem contains the unsolved problem on matrix pairs (i.e. the problem of simultaneously reducing to canonical form two linear operators on a finite-dimensional space), and algebras of tame type.
Basic problems studied in the representation theory of associative algebras are that of obtaining necessary and sufficient conditions for an algebra to belong to one of the types listed, as well as that of classifying the indecomposable representations in the finite and tame cases. In the general case these problems have not been solved. The description of algebras of finite or tame type and their representations has been obtained for algebras the square of whose radical equals zero (cf. [2], [4], [8]–[10]). The Brauer–Thrall problem has been solved, i.e. it has been proved that, over any field, an algebra of infinite type has indecomposable representations of arbitrary high dimension, while over a perfect field there are infinitely many dimensions in each of which there are infinitely many indecomposable representations (cf. [5], [7]). Any algebra of finite type over an algebraically closed field has a multiplicative basis, i.e. a basis for which the product of two arbitrary elements in it is either zero or belongs to the basis [6]. The problem of dividing the class of group algebras into tame and wild ones has been completely solved [1].
Strongly related with representations of associative algebras are representations of other objects: rings, partially ordered sets, lattices, boxes.
References
| [1] | V.M. Bondarenko, Yu.A. Drozd, "Representation type of finite groups" J. Soviet Math. , 20 : 6 (1982) pp. 2515–2528 Zap. Nauchn. Sem. Leningr. Univ. , 71 (1977) pp. 24–41 MR0472984 Zbl 0497.16015 |
| [2] | S.A. Kruglyak, "Representations of algebras the square of whose radical equals zero" J. Soviet Math. , 3 : 5 (1975) pp. 629–636 Zap. Nauchn. Sem. Leningr. Univ. , 28 (1972) pp. 60–69 |
| [3] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) MR0144979 Zbl 0131.25601 |
| [4] | L.A. Nazarova, "Representations of quivers of infinite type" Math. USSR Izv. , 7 : 4 (1973) pp. 749–792 Izv. Akad. Nauk SSSR Ser. Mat. , 37 : 4 (1973) pp. 752–791 MR0338018 Zbl 0298.15012 |
| [5] | U. Fischbacher, "Une nouvelle preuve d'un théorème de Nazarova et Roiter" C.R. Acad. Sci. Paris , 300 (1984) pp. 259–263 MR0785064 |
| [6] | R. Bautista, P. Gabriel, A. Roiter, L. Salmeron, "Representation finite algebras and multiplicative bases" Invent. Math. , 81 (1985) pp. 217–285 MR0799266 Zbl 0575.16012 |
| [7] | A.V. Roiter, "Unbounded dimensionality of indecomposable representations of an algebra with an infinite number of indecomposable representations" Math. USSR Izv. , 2 : 6 (1968) pp. 1223–1230 Izv. Akad. Nauk SSSR Ser. Mat. , 32 : 6 (1968) pp. 1275–1282 |
| [8] | V. Dlab, C. Ringel, "Indecomposable representations of graphs and algebras" , Amer. Math. Soc. (1976) MR0447344 Zbl 0332.16015 |
| [9] | P. Donovan, M.R. Freislich, "The representation theory of finite graphs and associated algebras" , Carleton Univ. (1974) MR0357233 Zbl 0304.08006 |
| [10] | P. Gabriel, "Unzerlegbare Darstellungen I" Manuscripta Math. , 6 : 1 (1972) pp. 71–103 MR0332887 Zbl 0232.08001 |
Comments
Thus, for an associative algebra $ A $ over the field $ k $ (with $ 1 $), a representation of $ A $ is an algebra homomorphism $ T: A \rightarrow \mathop{\rm End} _ {k} ( E) $, where $ E $ is a vector space over $ k $ and $ \mathop{\rm End} _ {k} ( E) $ denotes the $ k $-algebra of all (linear) endomorphisms of $ E $. A subrepresentation of the representation $ T: A \rightarrow \mathop{\rm End} _ {k} ( E) $ is given by a subspace $ E ^ \prime $ of $ E $ which is $ T ( a) $-invariant for all $ a \in A $, and, in this case, one obtains a representation on $ E / E ^ \prime $, called a quotient representation. Given a representation $ T : A \rightarrow \mathop{\rm End} _ {k} ( E) $ of $ A $, there is the dual (or contragredient) representation $ T ^ \star : A ^ { \mathop{\rm op} } \rightarrow \mathop{\rm End} _ {k} ( E ^ \star ) $ of the opposite algebra $ A ^ { \mathop{\rm op} } $ of $ A $ (this is the algebra on the underlying vector space of $ A $ with multiplication $ \star $ defined by $ a \star b = ba $); by definition, $ T ^ \star ( a) ( \varphi )( e) = \varphi ( T( a)( e)) $ for $ a \in A ^ { \mathop{\rm op} } = A $, $ e \in E $, $ \varphi \in E ^ \star = \mathop{\rm Hom} _ {k} ( E, k) $. Cf. also Contragredient representation.
Let $ T : A \rightarrow \mathop{\rm End} _ {k} ( E) $ be a representation; instead of $ T( a) ( e) $ for $ a \in A $, $ e \in E $, one often writes just $ ae $; in this way $ E $ becomes a left $ A $-module, and any left $ A $-module is obtained in this way. Given two representations $ T _ {1} : A \rightarrow \mathop{\rm End} _ {k} ( E _ {1} ) $ and $ T _ {2} : A \rightarrow \mathop{\rm End} _ {k} ( E _ {2} ) $, a mapping $ f $ from $ T _ {1} $ to $ T _ {2} $ is a linear transformation $ f : E _ {1} \rightarrow E _ {2} $ satisfying $ f( T _ {1} ( a) e) = T _ {2} ( a)( f( e)) $ for $ a \in A $, $ e \in E $, or, rewritten, $ f ( ae) = af( e) $; thus it is an $ A $-module homomorphism. If $ T _ {i} : A \rightarrow \mathop{\rm End} _ {k} ( E _ {i} ) $ is a family of representations, their direct sum is the representation $ T : A \rightarrow \mathop{\rm End} _ {k} ( E ) $, where $ E = \oplus _ {i} E _ {i} $ is the direct sum of vector spaces and $ T ( A) \mid _ {E _ {i} } = T _ {i} ( a) $, for all $ a \in A $. The category of all representations of $ A $, equivalently, the category of (left) $ A $-modules, is an Abelian category. Note that if $ e $ is a central idempotent of $ A $ (i.e. $ e ^ {2} = e \in A $ and $ ea = ae $ for all $ a \in A $) and $ X $ is an $ A $-module, then $ eX $ and $ ( 1- e) X $ are $ A $-modules, $ X $ is the direct sum of $ eX $ and $ ( 1- e) X $, and $ \mathop{\rm Hom} _ {A} ( eX, ( 1- e) X) = 0 $. On the other hand, $ A = A _ {1} \times A _ {2} $, where $ A _ {1} = Ae $, $ A _ {2} = A( 1- e) $, and one may regard $ eX $ as an $ A _ {1} $-module and $ ( 1- e) X $ as an $ A _ {2} $-module. Thus, dealing with representations of $ A $ one may assume that $ A $ is connected (that is, the only central idempotents of $ A $ are $ 0 $ and $ 1 $).
A representation of $ A $ is said to be simple (or irreducible) provided it is non-zero and the only proper subrepresentation is the zero representation. The Schur lemma asserts that the endomorphism ring of a simple representation is a division ring (cf. Ring with division). A representation $ X $ of $ A $ is said to be of finite length if there is a sequence of subrepresentations $ 0 = X _ {0} \subset X _ {1} \subset \dots \subset X _ {n} = X $ such that $ X _ {i} / X _ {i-1} $ is simple, for $ 1 \leq i \leq n $; such a sequence is called a composition series of $ X $, $ n $ is its length, and the factors $ X _ {i} / X _ {i-1} $ are called the composition factors (cf. also Composition sequence). If a representation has a composition series, then any two composition series have the same length, and there is a bijection between the composition factors of the two series (the Jordan–Hölder theorem). This may be formulated also as follows: the Grothendieck group of all finite-length representations modulo exact sequences is the free Abelian group on the set of isomorphism classes of simple representations. A representation of $ A $ is called semi-simple if it is a direct sum of simple representations, or, equivalently, if any subrepresentation is a direct summand.
A representation of $ A $ is said to be indecomposable if it cannot be written as the direct sum of two non-zero representations. If $ X $ is an indecomposable representation of $ A $ of finite length, then its endomorphism ring $ \mathop{\rm End} ( _ {A} X) $ is a local ring. For a finite direct sum of representations with local endomorphism rings, all direct sum decompositions into indecomposable representations are equivalent (the Krull–Schmidt theorem, cf. Krull–Remak–Schmidt theorem). It follows that the Grothendieck group of all finite-length modules modulo split exact sequences is the free Abelian group on the set of isomorphism classes of indecomposable representations.
The algebra $ A $ is said to be representation-finite if there are only finitely many isomorphism classes of indecomposable representations of $ A $; it is called tame if it is not representation-finite but all families of indecomposable representations are $ 1 $-parametric, and wild if the category $ A $-mod of all finite-dimensional $ A $-modules involves the classification problem for pairs of square matrices up to simultaneous equivalence [a7]. Let $ A $ be a finite-dimensional algebra. If the dimension of each finite-dimensional indecomposable representation is bounded, then $ A $ is representation-finite (the first Brauer–Thrall conjecture, solved by V.A. Roiter [7]) and any representation is the direct sum of finite-dimensional indecomposable ones [a12]. The second Brauer–Thrall conjecture asserts that if $ A $ is not representation-finite and $ k $ is an infinite field, then there are infinitely many isomorphism classes of dimension $ d $, for infinitely many $ d $. The conjecture has been solved for perfect $ k $ by R. Bautista [a3] and K. Bongartz [a5], see also [a11]. If $ A $ is not representation-finite, then $ A $ is either tame or wild and not both (Drozd's theorem [a7]). Certain minimal representation-infinite algebras have been classified by D. Happel and D. Vossieck [a9], and questions concerning minimal representation-infinite algebras over algebraically closed fields can be transferred to this list; in particular, one gets in this way a criterion for finite-representation type [a4], [a8]. In general, questions concerning finite-dimensional algebras over algebraically closed fields are treated by considering quivers with relations (see Quiver).
Let $ A $ be a finite-dimensional algebra. If $ A $ has no non-zero nilpotent ideal, then $ A $ is said to be semi-simple. The algebra $ A $ is semi-simple if and only if any representation of $ A $ is semi-simple; in this case, the simple representations are just the indecomposable summands of the regular representation of $ A $. In general, let $ N $ be the radical of $ A $ (cf. Radical of rings and algebras), it is the maximal nilpotent ideal of $ A $ and $ A / N $ is semi-simple. The simple representations of $ A $ are the indecomposable summands of $ A /N $; up to isomorphism, there are only finitely many. The indecomposable projective representations are the direct summands of the regular representation of $ A $, the indecomposable injective representations are the duals of the regular representation of $ A ^ { \mathop{\rm op} } $. Any indecomposable projective representation of $ A $ has a unique simple quotient representation, any indecomposable injective representation of $ A $ has a unique simple subrepresentation; in this way one obtains a bijection between the isomorphism classes of the simple $ A $-modules and the indecomposable projective $ A $-modules, as well as the indecomposable injective $ A $-modules.
The basic notions of modern representation theory are due to M. Auslander and I. Reiten [a1]: Given any indecomposable $ A $- module $ Z $, there is a mapping $ g: Y \rightarrow Z $ which is minimal right almost split: it is not a split epimorphism, given any mapping $ g ^ \prime : Y ^ \prime \rightarrow Z $ which is not a split endomorphism, there is a $ y : Y ^ \prime \rightarrow Y $ with $ gy = y ^ \prime $, and given $ e : Y \rightarrow Y $ with $ ge = g $, then $ e $ is an automorphism. If $ Z $ is projective, take for $ Y $ its maximal submodule and for $ g $ the inclusion mapping. For $ Z $ non-projective, the minimal right almost split mapping $ g $ is surjective, its kernel $ X $ is indecomposable (and not injective), and the inclusion mapping $ f: X \rightarrow Y $ is minimal left almost split (defined by the dual properties); also, any indecomposable non-injective $ A $- module occurs in this way as $ X $. These exact sequences $ 0 \rightarrow X \rightarrow ^ {f} Y \rightarrow ^ {g} Z \rightarrow 0 $ with $ f $ minimal left almost split and $ g $ minimal right almost split are called almost-split sequences (or Auslander–Reiten sequences). They are uniquely determined by $ X $ and by $ Z $; given $ Z $, the corresponding $ A $-module $ X = \tau Z $ can be calculated as follows: Take a minimal projective representation $ P _ {1} \rightarrow ^ {p} P _ {0} \rightarrow Z \rightarrow 0 $ of $ Z $, let $ \mathop{\rm Tr} Z = \mathop{\rm Hom} _ {A} ( p, A) $, then $ X = ( \mathop{\rm Tr} Z) ^ \star $; the construction $ \tau $ is called the Auslander–Reiten translation.
The Auslander–Reiten quiver $ \Gamma _ {A} $ of $ A $ has as vertices the isomorphism classes $ [ X] $ of the finite-dimensional indecomposable $ A $-modules $ X $, and there is an arrow $ [ X] \rightarrow [ Y] $ provided there exists an irreducible mapping $ X \rightarrow Y $ (note that a mapping $ f: X \rightarrow Y $ with $ X, Y $ indecomposable is called irreducible if $ f $ is not invertible and given a factorization $ X \rightarrow ^ {f _ {1} } I \rightarrow ^ {f _ {2} } Y $ of $ f $, then $ f _ {1} $ is a split monomorphism or $ f _ {2} $ is a split epimorphism); in addition, $ \Gamma _ {A} $ is equipped with the Auslander–Reiten translation $ \tau $. The meshes of the Auslander–Reiten quiver are as follows: Given an indecomposable non-projective representation $ Z $ and an indecomposable representation $ Y $, there is an irreducible mapping $ Y \rightarrow Z $ if and only if there is an irreducible mapping $ \tau : Z \rightarrow Y $ (this is the case if and only if $ Y $ is a direct summand of $ E $, where $ E $ is the middle term of the almost-split sequence $ 0 \rightarrow \tau Z \rightarrow E \rightarrow Z \rightarrow 0 $). The Auslander–Reiten quiver of $ A $ is an important combinatorial invariant of $ A $, often one may recover $ A $ from $ \Gamma _ {A} $. In case $ A $ is connected and $ \Gamma _ {A} $ has a finite component, $ A $ is representation-finite (Auslander's theorem, [a1]). Deleting from $ \Gamma _ {A} $ the vertices of the form $ [ \tau ^ {n} I ] $ with $ I $ indecomposable injective, $ n \in \mathbf N $, and $ [ \tau ^ {-} n P ] $ with $ P $ indecomposable projective, $ n \in \mathbf N $, one obtains the stable Auslander–Reiten quiver $ \Gamma _ {A} ^ {s} $. For $ A $ representation-finite, the components of $ \Gamma _ {A} ^ {s} $ are related to Dynkin diagrams (cf. Dynkin diagram) [a13], [a10]. Using covering theory [a6], the study of representation-finite algebras can be reduced to that of representation-directed algebras (an algebra is called representation directed if there are only finitely many indecomposable representations $ X _ {1}, \dots, X _ {n} $ and they can be ordered so that $ \mathop{\rm Hom} ( X _ {i} , X _ {j} ) = 0 $ for $ i > j $). The Auslander–Reiten quiver of a representation-directed algebra $ A $ (and therefore the category $ A $-mod) can be constructed effectively [a14].
References
| [a1] | M. Auslander, "Applications of morphisms determined by objects" R. Gordon (ed.) , Representation Theory of Algebras , M. Dekker (1978) pp. 245–327 |
| [a2] | M. Auslander, I. Reiten, "Representation theory of Artin algebras III" Comm. in Algebra (1975) pp. 239–294 MR0379599 Zbl 0331.16027 |
| [a3] | R. Bautista, "On algebras of strongly unbounded representation type" Comment. Math. Helv. , 60 (1985) pp. 392–399 MR0814146 Zbl 0584.16017 |
| [a4] | K. Bongartz, "A criterion for finite representation type" Math. Ann. , 269 (1984) pp. 1–12 MR0756773 Zbl 0552.16012 |
| [a5] | K. Bongartz, "Indecomposables are standard" Comment. Math. Helv. , 60 (1985) pp. 400–410 MR0814147 Zbl 0591.16014 |
| [a6] | K. Bongartz, P. Gabriel, "Covering spaces in representation theory" Invent. Math. , 65 (1981) pp. 381–387 MR0643558 Zbl 0482.16026 |
| [a7] | Yu.A. Drozd, "Tame and wild matrix problems" V. Dlab (ed.) P. Gabriel (ed.) , Representation Theory II , Lect. notes in math. , 832 , Springer (1980) pp. 242–258 MR0607157 Zbl 0457.16018 |
| [a8] | P. Dräxler, "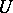 -Fasersummen in darstellungsendlichen Algebren" J. Algebra , 113 (1988) pp. 430–437 MR0929771 Zbl 0659.16020 -Fasersummen in darstellungsendlichen Algebren" J. Algebra , 113 (1988) pp. 430–437 MR0929771 Zbl 0659.16020 |
| [a9] | D. Happel, D. Vossieck, "Minimal algebras of infinite representation type with preprojective component" Manuscripta Math. , 42 (1983) pp. 221–243 MR0701205 Zbl 0516.16023 |
| [a10] | D. Happel, U. Preiser, C.M. Ringel, "Vinberg's characterization of Dynkin diagrams using subadditive functions with application to DTr-periodic modules" V. Dlab (ed.) P. Gabriel (ed.) , Representation Theory II , Lect. notes in math. , 832 , Springer (1980) pp. 280–294 |
| [a11] | L.A. Nazarova, A.V. Roiter, "Categorical matrix problems and the Brauer–Thrall conjecture" , Kiev (1973) (In Russian) |
| [a12] | C.M. Ringel, H. Tachikawa, "QF-3 rings" J. Reine Angew. Math. , 272 (1975) pp. 49–72 MR0379578 Zbl 0318.16006 |
| [a13] | Chr. Riedtmann, "Algebren, Darstellungsköcher, Überlagerungen, und zurück" Comment. Math. Helv. , 55 (1980) pp. 199–224 MR0576602 Zbl 0444.16018 |
| [a14] | C.M. Ringel, "Tame algebras and integral quadratic forms" , Lect. notes in math. , 1099 , Springer (1984) MR0774589 Zbl 0546.16013 |
| [a15] | D. Happel, "Triangulated categories in representation theory of finite dimensional algebras" , London Math. Soc. (1988) MR935124 Zbl 0635.16017 |
C.M. Ringel
Representation of an associative algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Representation_of_an_associative_algebra&oldid=52581