Recursive set theory

A branch of the theory of recursive functions (cf. Recursive function) that examines and classifies subsets of natural numbers from the point of view of algorithms, and also studies the structures arising as a result of such a classification. For each subset $ A $ of the set of all natural numbers $ \mathbf N $, the following decision problem can be formulated: Is there an algorithm that permits one to decide, for any $ x \in \mathbf N $, whether or not $ x $ is a member of $ A $?

The mathematical posing of problems of this kind, and the development of recursive set theory, only became possible in the 1940's after the successful formalization of the intuitive concept of an (algorithmically) computable function. The range of values of such functions forms the family of recursively-enumerable sets (cf. also Enumerable set). Sets for which the problem formulated above is solvable are called recursive. In fact, $ A $ is recursive if and only if $ A $ and $ \mathbf N \setminus A $ are both recursively enumerable. The first examples of non-recursive recursively-enumerable sets turned out to be the so-called creative sets: a recursively-enumerable set $ K $ is called creative if there is a computable function, defined on the numbers of all recursively-enumerable sets $ A $ not intersecting $ K $ and giving a number belonging to $ \mathbf N \setminus ( K \cup A) $. At the same time as creative sets, other non-recursive recursively-enumerable sets were also discovered, in particular the simple ones. A recursively-enumerable set is called simple if it has an infinite complement not containing an infinite recursively-enumerable set. In this way arises the specific problem of classifying decision problems of recursively-enumerable sets. One instrument for such a classification is the concept of reducibility. On an intuitive level, a set $ A $ is reducible to a set $ B $ if there is an algorithm that would solve the problem of membership of numbers for $ A $ if there is information about membership of certain natural numbers for $ B $. In this case $ A $ is in the specific sense "recursive" relative to $ B $, and the ordinary recursive sets are "recursive" relative to any set. In its widest sense this reducibility (the detailed formulation of which is quite complex) is called Turing or $ T $- reducibility. By imposing one or more restrictions on the algorithm involved in the concept of reducibility, the definition of other reducibilities may be arrived at: for example, $ 1 $-, many-one, $ btt $-, or $ tt $- reducibilities. In particular, $ A $ is many-one reducible to $ B $ if there is a total computable function $ f $ such that for all $ x $ in $ \mathbf N $,

$$ x \in A \iff f( x) \in B. $$

If $ f $ can be selected injectively, then it is said that $ A $ is $ 1 $- reducible to $ B $.

A generalization of many-one reducibility is truth-table reducibility ( $ tt $- reducibility). A set $ A $ is $ tt $- reducible to a set $ B $ if there is an algorithm that gives, for each $ x $, a collection of numbers $ \langle t _ {1} ^ {x} \dots t _ {n(} x) ^ {x} \rangle $ and a Boolean function $ \beta _ {x} ( y _ {1} \dots y _ {n(} x) ) $ such that

$$ x \in A \iff \beta _ {x} ( \chi ( t _ {1} ^ {x} ) \dots \chi ( t _ {n(} x) ^ {x} )) = 1, $$

and $ \chi ( t) = 1 $ if $ t \in B $ and $ \chi ( t) = 0 $ in the opposite case. If $ A $ is truth-table reducible to $ B $ in such a way that $ n( x) $ will be bounded by a certain constant, then $ A $ is said to be bounded truth-table reducible ( $ btt $- reducible) to $ B $. Let $ r $ be a certain reducibility. Let $ A \leq _ {r} B $ denote that the set $ A $ is $ r $- reducible to $ B $. The relation $ \leq _ {r} $ is a pre-order. If it is assumed that

$$ A \equiv _ {r} B \iff ( A \leq _ {r} B \& B \leq _ {r} A), $$

then $ \equiv _ {r} $ will be an equivalence relation, whose individual classes are called $ r $- degrees (and recursively-enumerable $ r $- degrees if the class contains a recursively-enumerable set). Turing degrees are well known in the literature as degrees of undecidability (cf. Degree of undecidability). The relation $ \leq _ {r} $ generates a partial order of all $ r $- degrees. A reducibility $ r ^ \prime $ is weaker than $ r $ if $ A \leq _ {r} B $ implies $ A \leq _ {r ^ \prime } B $. Partially ordered sets of $ r $- degrees for many-one and weaker reducibilities form upper semi-lattices (which is false for $ 1 $- degrees), having a smallest element $ \mathbf 0 $, the $ r $- degree of recursive sets. If one restricts to the study of recursively-enumerable $ r $- degrees, they have also a largest element $ \mathbf 1 $, called a complete $ r $- degree. Recursively-enumerable sets contained in a complete $ r $- degree are called $ r $- complete. Minimal $ r $- degrees are those having only one strictly smaller $ r $- degree, in fact $ \mathbf 0 $.

The study of reducibilities has been developed in two directions. The first question involved the description of the upper semi-lattices of the degrees relative to the defined reducibility. The famous example of this type of problem is Post's problem [1]: Is it true that all non-recursive recursively-enumerable sets have the same degree of undecidability? Or, in other words, is it true that the semi-lattice of recursively-enumerable degrees of undecidability consists of only two elements? A negative solution to this problem has been found [2]. Solutions to such problems on the structure of the upper semi-lattices of recursively-enumerable many-one $ tt $-, and $ T $- degrees were definite landmarks in the study of reducibilities. At the beginning of the 1960s it was proved that the semi-lattice of $ T $- degrees (below semi-lattices of recursively-enumerable degrees are meant) is not a lattice and does not have minimal elements. At that time the existence of minimal many-one degrees was noted, and it was shown that a complete many-one degree is not the least upper bound of two incomparable many-one degrees. Later it became clear that this fact did not hold for $ btt $- and weaker reducibilities. Yu.L. Ershov [4] proved that the upper semi-lattice of many-one degrees is not a lattice and that among some of its elements there are no minimal ones. Similar results, as well as the existence of minimal elements, were obtained for $ btt $- and $ tt $- degrees [5]. It was established that the elementary theories of semi-lattices of many-one, $ btt $-, $ tt $-, $ T $- and several other degrees are mutually different.

The second direction was connected with questions about what are $ r $- degrees, how many of them are there, and how are they distributed in degrees of a relatively weaker reducibility than $ r $? In particular, a complete $ T $- ( $ tt $-, $ btt $-) degree contains a countable number of recursively-enumerable $ tt $- ( $ btt $-, many-one, respectively) degrees. On the other hand, there are non-recursive $ T $- ( $ btt $-) degrees consisting of one $ tt $- (many-one) degree, but each non-recursive $ tt $- degree contains at least two $ btt $- degrees.

There are other approaches to the study of recursively-enumerable sets, not related to the concept of reducibility. One of them is contained in the following: All recursively-enumerable sets, together with the operations of union and intersection, form a lattice $ {\mathcal E} $. A property of recursively-enumerable sets is called lattice-theoretic if it is preserved under all automorphisms of $ {\mathcal E} $. Such, for example, are the properties of "being recursive" , "simple" or "maximal" . A recursively-enumerable set $ A $ is called maximal ( $ r $- maximal) if its complement is infinite and cannot be partitioned by a recursively-enumerable set (a recursive set, respectively) into two infinite parts. Examples of classical results connected with the study of $ {\mathcal E} $ are the theorems on the existence of maximal sets and on the possibility of partitioning any non-recursive recursively-enumerable set into two non-recursive recursively-enumerable sets (see [2]), as well as the theorem on the existence of $ r $- maximal sets without maximal supersets (see [3]).

The concept of a maximal set arose from the hope that such sets would be not $ T $- complete. This could have been a natural solution to Post's problem. E. Post himself, by imposing increasingly severe restrictions on the complements of recursively-enumerable sets, defined classes of hyper-simple and hyper-hyper-simple sets, and proved that hyper-simple sets cannot be $ tt $- complete. Thus, a recursively-enumerable set $ A $ with an infinite complement is called hyper-simple (hyper-hyper-simple) if there is no computable sequence of mutually non-intersecting finite (recursively-enumerable) sets, each of which also has non-empty intersection with the complement of $ A $. The definition of these classes of sets is not given in lattice-theoretic terms; in fact it has been shown that "being hyper-simple" is not a lattice-theoretic property. It has been proved, however, that a recursively-enumerable set $ A $ with an infinite complement is hyper-hyper-simple if and only if for any recursively-enumerable set $ B $ there is a recursive set $ R $ such that $ R \subseteq B $ and $ ( B \setminus A) \subseteq R $, i.e. the property of "being hyper-hyper-simple" proved to be lattice-theoretic. A hyper-hyper-simple set without maximal supersets has been constructed [3] and it was also proved that for any non-recursive recursively-enumerable set $ A $ there is an automorphism $ \Phi $ of the lattice $ {\mathcal E} $ such that $ \Phi ( A) $ is a $ T $- complete set [6]. Thus, the hope of finding a lattice-theoretic property that would not contain recursive and $ T $- complete sets proved to be in vain.

There is also the view (in line with [7]) according to which recursive set theory must examine properties of subsets of $ \mathbf N $ that are preserved under recursive permutations. In accordance with this, two sets $ A $ and $ B $ can thus be said to have the same recursive equivalence type if there is an injective computable function $ f $ such that $ f( A) = B $ and $ f ^ { - 1 } ( B) = A $. Those types of recursive equivalences that do not contain sets with infinite recursively-enumerable subsets are called isols. Once convenient operations of addition and multiplication had been defined for isols, the "arithmetic" of isols began to develop.

The study of properties of recursively-enumerable sets and reducibilities is not only linked with other directions in the theory of recursive functions, but it also finds application in logic, model theory and algebra. Recursive set theory has its own methods of research. The most well-known is the so-called priority method, by which profound results have been obtained.

References

[1]	E.L. Post, "Recursively enumerable sets of positive integers and their decision problems" Bull. Amer. Math. Soc. , 50 (1944) pp. 284–316
[2]	R.M. Friedberg, "Three theorems on recursive enumeration: I. Decomposition, II. Maximal set, III. Enumeration without duplication" J. Symbolic Logic , 23 (1958) pp. 309–316
[3]	A.H. Lachlan, "On the lattice of recursively enumerable sets" Trans. Amer. Math. Soc. , 130 : 1 (1968) pp. 1–37
[4]	Yu.L. Ershov, "Hyperhypersimple 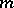-degrees" Algebra and Logic , 8 : 5 (1969) pp. 298–315 Algebra i Logika , 8 : 5 (1969) pp. 523–552
[5]	A.N. Degtev, "Reducibilities of tabular type in the theory of algorithms" Russian Math. Surveys , 34 : 3 (1979) pp. 155–192 Uspekhi Mat. Nauk , 34 : 3 (1979) pp. 137–168
[6]	R.J. Soare, "Recursively enumerable sets and degrees" Bull Amer. Math. Soc. , 84 : 6 (1978) pp. 1149–1181
[7]	J.C.E. Dekker, J. Myhill, "Recursive equivalence types" Publ. Math. Univ. Calif. , 3 : 3 (1960) pp. 67–213
[8]	A.I. Mal'tsev, "Algorithms and recursive functions" , Wolters-Noordhoff (1970) (Translated from Russian)
[9]	H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) pp. 164–165

Comments

Since algorithms are describable in one language or the other, one can systematically assign natural numbers to descriptions of algorithms simply by enumerating the expressions of the language under consideration according to (first) length and (next) lexicographically (cf. Recursion). Therefore, the classes of computable functions and of recursively-enumerable sets can also be so enumerated: the $ n $- th computable function simply is the function computed by the algorithm to which the number $ n $ is assigned, and the $ n $- th recursively-enumerable set is the range of the $ n $- th computable function. Here $ n $ is called the number of the recursively-enumerable set (cf. also Recursive function).

The (negative) solution of Post's problem mentioned above is usually known as the Muchnik–Friedberg theorem (cf. [2], [a1], [a4]). This is the result that specifically gave rise to the priority methods. They, A.A. Muchnik and R.M. Friedberg, arrived at a solution independently, cf. also Degree of undecidability.

See also Algorithmic reducibility; Productive set; Turing machine.

References

[a1]	A.A. Muchnik, "On the unsolvability of the reducibility problem in the theory of algorithms" Dokl. Akad. Nauk SSSR , 108 : 2 (1956) pp. 194–197 (In Russian)
[a2]	R.I. Soare, "Recursively enumerable sets and degrees, a study of computable functions and generated sets" , Springer (1987)
[a3]	J. Barwise (ed.) , Handbook of mathematical logic , North-Holland (1978)
[a4]	R.M. Friedberg, "Two recursively enumerable sets of incomparible degrees of unsolvability (solution of Post's problem)" Proc. Nat. Acad. Sci. USA , 43 (1957) pp. 236–238