Real closed field
An ordered field $ K $
for which no non-trivial algebraic extension (cf. Extension of a field) can be ordered. E. Artin and O. Schreier ([a1]) characterized real closed fields to be the fields $ K $
for which the algebraic closure (cf. Algebraically closed field) is a non-trivial finite extension; in this case, it is of degree $ 2 $
and obtained by adjoining the square root of $ - 1 $.
Every ordered field $ K $
has an algebraic extension which is real closed, unique up to order-preserving isomorphism over $ K $.
It is called the real closure of $ K $.
Model theory.
In 1940, A. Tarski proved that the elementary theory of all real closed fields is complete; this is known as the Tarski principle. It implies that, roughly speaking, Euclidean geometry remains the same if the field $ \mathbf R $ of real numbers is replaced by any other real closed field, at least for those theorems which can be formulated in a first-order language of ordered fields (and these are many geometrical theorems). This is the real analogue of the elementary version of the Lefschetz principle (cf. Transfer principle).
Tarski also proved that the elementary theory of real closed fields admits elimination of quantifiers (cf. [a11]). In 1956, A. Robinson deduced model completeness by simple model-theoretic techniques from the uniqueness of the real closure and the fact that the order of an extension $ K ( x ) $ of a real closed field $ K $ with $ x \notin K $ is uniquely determined by the cut $ ( \{ {c \in K } : {c < x } \} , \{ {d \in K } : {x < d } \} ) $ that $ x $ induces in $ K $. This can be adapted to prove elimination of quantifiers.
The theory of real closed fields can be recursively axiomatized (cf. Axiomatized class) in a first-order language of ordered rings or fields (cf. Structure). To the axioms for ordered fields, one only has to add an infinite axiom scheme expressing the sign change property, which says that every polynomial must have a root in a given interval where it changes sign; for $ \mathbf R $ this is the content of the intermediate value theorem (cf. Cauchy theorem). Since the theory is complete, the recursive axiomatization yields decidability. The completeness also shows that all first-order theorems and axioms of Euclidean geometry are consequences of the axioms given in this axiomatization.
Further, it follows from work of G.L. Cherlin and M. Dickmann (1983) that the theory of real closed fields with a convex valuation ring admits elimination of quantifiers in the language of ordered fields enriched by a unary relation symbol for being an element of the valuation ring (cf. Model theory of valued fields).
Hilbert's 17th problem and a real Nullstellensatz.
Artin gave a positive answer to Hilbert's 17th problem in [a1], using a generalization of the Sturm theorem. He proved that if $ K $ is real closed, $ f \in K [ X _ {1} \dots X _ {n} ] $ and $ f ( a _ {1} \dots a _ {n} ) \geq 0 $ for all $ a _ {1} \dots a _ {n} \in K $, then $ f $ is a sum of squares in $ K ( X _ {1} \dots X _ {n} ) $. (Note that the squares have to be taken over elements of the rational function field.) Hilbert's original 17th problem asks for an analogous result with $ K $ replaced by the field of rational numbers $ \mathbf Q $; the above also holds for this case since $ K $ can be replaced by any ordered field which is dense in its real closure and admits a unique order.
The theorem was reproved by A. Robinson in 1955 using model completeness, which can also be used to prove a real version of Hilbert's Nullstellensatz (cf. Hilbert theorem). There are many such versions, due to several authors. The following is known as the Dubois Nullstellensatz (D.W. Dubois, 1969): If $ K $ is an ordered field, $ I \subset K [ X _ {1} \dots X _ {n} ] $ an ideal and $ f \in K [ X _ {1} \dots X _ {n} ] $ such that every common root of all polynomials in $ I $ in the real closure of $ K $ is also a root of $ f $, then $ f $ lies in the real radical of $ I $. The real radical is defined to be the set of all $ f $ for which $ f ^ {2m } + s \in I $ for some $ m \in \mathbf N $, where $ s = \sum c _ {i} g _ {i} ^ {2} $ is a sum of squares of elements $ g _ {i} \in K [ X _ {1} \dots X _ {n} ] $ with positive coefficients $ c _ {i} \in K $.
See also Elimination of quantifiers and $ p $- adically closed field.
References
| [a1] | E. Artin, O. Schreier, "Algebraische Konstruktion reeller Körper; Über die Zerlegung definiter Funktionen in Quadrate; Eine Kennzeichnung der reell abgeschlossenen Körper" Abh. Math. Sem. Univ. Hamburg , 5 (1927) pp. 85–99; 100–115; 225–231 Zbl 52.0120.05 |
| [a2] | E. Becker, R. Berr, F. Delon, D. Gondard, "Hilbert's 17th problem for sums of 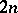 -th powers" J. Reine Angew. Math. , 450 (1994) pp. 139–157 MR1273958 -th powers" J. Reine Angew. Math. , 450 (1994) pp. 139–157 MR1273958 |
| [a3] | J. Bochnak, M. Coste, M.-F. Roy, "Géométrie algébrique réelle" , Springer (1987) MR0949442 Zbl 0633.14016 |
| [a4] | C. Delzell, "Continuous piecewise-polynomial functions which solve Hilbert's 17th problem" J. Reine Angew. Math. , 440 (1993) pp. 157–173 MR1225962 |
| [a5] | M. Knebusch, "An invitation to real spectra" , Quadratic and Hermitean forms, Conf. Hamilton/Ont. 1983 , CMS Conf. Proc. , 4 , Amer. Math. Soc. (1984) pp. 51–105 MR0776447 Zbl 0586.14015 |
| [a6] | M. Knebusch, C. Scheiderer, "Einführung in die reelle Algebra" , Vieweg (1989) MR1029278 Zbl 0732.12001 |
| [a7] | M. Knebusch, C. Scheiderer, "Semi-algebraic topology in the last 10 years; Real algebra and its applications to geometry in the last 10 years: some major developments and results" M. Coste (ed.) M.F. Roy (ed.) , Real algebraic geometry, Proc. Conf. Rennes 1991 , Lecture Notes in Mathematics , 1524 , Springer (1992) pp. 1–36; 75–96 |
| [a8] | T. Y. Lam, "The theory of ordered fields" B. McDonald (ed.) , Ring Theory and Algebra III , Lecture Notes in Pure and Applied math. , 55 , New York (1980) pp. 1–152 MR0584611 Zbl 0442.12024 |
| [a9] | A. Prestel, "Lectures on formally real fields" , Lecture Notes in Mathematics , 1093 , Springer (1984) MR0769847 Zbl 0548.12011 |
| [a10] | S. Prieß-Crampe, "Angeordnete Strukturen. Gruppen, Körper, projektive Ebenen" , Ergebnisse der Mathematik und ihrer Grenzgebiete , 98 , Springer (1983) Zbl 0558.51012 |
| [a11] | A. Tarski, J.C.C. McKinsey, "A decision method for elementary algebra and geometry" , Univ. California Press (1951) MR0044472 Zbl 0044.25102 |
| [a12] | E. Becker, "Theory of real fields and sums of powers" , Springer (to appear) |
Real closed field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Real_closed_field&oldid=48449