Projective space
The collection of all subspaces of an incidence system $ \pi = \{ {\mathcal P} , {\mathcal L} , \textrm{ I } \} $,
where the elements of the set $ {\mathcal P} $
are called points, the elements of the set $ {\mathcal L} $
are called lines and I is the incidence relation. A subspace of $ \pi $
is defined to be a subset $ S $
of $ {\mathcal P} $
for which the following condition holds: If $ p , q \in S $
and $ p \neq q $,
then the set of points of the line passing through $ p $
and $ q $
also belongs to $ S $.
The incidence system $ \pi $
satisfies the following requirements:
1) for any two different points $ p $ and $ q $ there exists a unique line $ L $ such that $ p \textrm{ I } L $ and $ q \textrm{ I } L $;
2) every line is incident to at least three points;
3) if two different lines $ L $ and $ M $ intersect at a point $ p $ and if the following four relations hold: $ q \textrm{ I } L $, $ r \textrm{ I } L $, $ s \textrm{ I } M $, $ l \textrm{ I } M $, then the straight lines passing through the pairs of points $ r , l $ and $ s , q $ intersect.
A subspace $ S $ is generated by a set $ s $ of points in $ {\mathcal P} $( written $ S = \langle s \rangle $) if $ S $ is the intersection of all subspaces containing $ s $. A set $ s $ of points is said to be independent if for any $ x \in s $ one has $ x \notin \langle s \setminus \{ x \} \rangle $. An ordered maximal and independent set of points of a subspace $ S $ is called a basis of $ S $, and the number $ d ( S) $ of its elements is called the dimension of the subspace $ S $. A subspace of dimension $ 0 $ is a point, a subspace of dimension $ 1 $ is a projective straight line, a subspace of dimension $ 2 $ is called a projective plane.
In a projective space the operations of addition and intersection of spaces are defined. The sum $ P _ {m} + P _ {k} $ of two subspaces $ P _ {m} $ and $ P _ {k} $ is defined to be the smallest of the subspaces containing both $ P _ {m} $ and $ P _ {k} $. The intersection $ P _ {m} \cap P _ {k} $ of two subspaces $ P _ {m} $ and $ P _ {k} $ is defined to be the largest of the subspaces contained in both $ P _ {m} $ and $ P _ {k} $. The dimensions of the subspaces $ P _ {m} $, $ P _ {k} $, of their sum, and of their intersection are connected by the relation
$$ m + k = d ( P _ {m} \cap P _ {k} ) + d ( P _ {m} + P _ {k} ) . $$
For any $ P _ {m} $ there is a $ P _ {n-m- 1} $ such that $ P _ {m} \cap P _ {n-m- 1}= P _ {-1} = \emptyset $ and $ P _ {m} + P _ {n-m- 1} = P _ {n} $( $ P _ {n-m- 1} $ is a complement of $ P _ {m} $ in $ P _ {n} $), and if $ P _ {m} \subset P _ {r} $, then
$$ ( P _ {m} + P _ {k} ) \cap P _ {r} = P _ {m} + P _ {k} \cap P _ {r} $$
for any $ P _ {k} $( Dedekind's rule), that is, with respect to the operation just introduced the projective space is a complemented modular lattice.
A projective space of dimension exceeding two is Desarguesian (see Desargues assumption) and hence is isomorphic to a projective space (left or right) over a suitable skew-field $ k $. The (for example) left projective space $ P _ {n} ^ {l} ( k) $ of dimension $ n $ over a skew-field $ k $ is the collection of linear subspaces of an $ ( n+ 1) $- dimensional left linear space $ A _ {n+1} ^ {l} ( k) $ over $ k $; the points of $ P _ {n} ^ {l} ( k) $ are the lines of $ A _ {n+1} ^ {l} ( k) $, i.e. the left equivalence classes of rows $ ( x _ {0} \dots x _ {n} ) $ consisting of elements of $ k $ which are not simultaneously equal to zero (two rows $ ( x _ {0} \dots x _ {n} ) $ and $ ( y _ {0} \dots y _ {n} ) $ are left equivalent if there is a $ \lambda \in k $ such that $ x _ {i} = \lambda y _ {i} $, $ i = 0 \dots n $); the subspaces $ P _ {m} ^ {l} ( k) $, $ m = 1 \dots n $, are the $ ( m+ 1) $- dimensional subspaces $ A _ {m+1}^ {l} ( k) $. It is possible to establish a correspondence between a left $ P _ {n} ^ {l} ( k) $ and a right $ P _ {n} ^ {r} ( k) $ projective space under which to a subspace $ P _ {s} ^ {l} ( k) $ corresponds $ P _ {n-s- 1} ^ {r} ( k) $( the subspaces $ P _ {s} ^ {l} ( k) $ and $ P _ {n-s- 1} ^ {r} ( k) $ are called dual to one another), to an intersection of subspaces corresponds a sum, and to a sum corresponds an intersection. If an assertion based only on properties of linear subspaces, their intersections and sums is true for $ P _ {n} ^ {l} ( k) $, then the corresponding assertion is true for $ P _ {n} ^ {r} ( k) $. This correspondence between the properties of the spaces $ P _ {n} ^ {r} ( k) $ and $ P _ {n} ^ {l} ( k) $ is called the duality principle for projective spaces (see [2]).
A finite skew-field is necessarily commutative; consequently, a finite projective space of dimension exceeding two and of order $ q $ is isomorphic to the projective space $ \mathop{\rm PG} ( n , q ) $ over the Galois field. The finite projective space $ \mathop{\rm PG} ( n , q ) $ contains $ ( q ^ {n+1} - 1 ) / ( q - 1 ) $ points and $ \prod_{i=0}^ {r} ( q ^ {n+1- i} - 1 ) / ( q ^ {r+1- i} - 1 ) $ subspaces of dimension $ r $( see [4]).
A collineation of a projective space is a permutation of its points that maps lines to lines so that subspaces are mapped to subspaces. A non-trivial collineation of the projective space has at most one centre and at most one axis. The group of collineations of a finite projective space $ \mathop{\rm PG} ( n , p ^ {h} ) $ has order
$$ hp ^ {hn( n+ 1)/2} \prod_{i=1} ^ { n+1} ( p ^ {hi} - 1 ) . $$
Every projective space $ \mathop{\rm PG} ( n , q ) $ admits a cyclic transitive group of collineations (see [3]).
A correlation $ \delta $ of a projective space is a permutation of subspaces that reverses inclusions, that is, if $ S \subset T $, then $ S ^ \delta \supset T ^ \delta $. A projective space admits a correlation only if it is finite-dimensional. An important role in projective geometry is played by the correlations of order two, also called polarities (Polarity).
References
| [1] | E. Artin, "Geometric algebra" , Interscience (1957) MR1529733 MR0082463 Zbl 0077.02101 |
| [2] | W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , 1 , Cambridge Univ. Press (1947) MR0028055 Zbl 0796.14002 Zbl 0796.14003 Zbl 0796.14001 Zbl 0157.27502 Zbl 0157.27501 Zbl 0055.38705 Zbl 0048.14502 |
| [3] | R. Dembowski, "Finite geometries" , Springer (1968) pp. 254 MR0233275 Zbl 0159.50001 |
| [4] | B. Segre, "Lectures on modern geometry" , Cremonese (1961) MR0131192 Zbl 0095.14802 |
Comments
The real and complex projective spaces $ \mathbf P _ {n} ( \mathbf R ) $, respectively $ \mathbf P _ {n} ( \mathbf C ) $, of all real, respectively complex, lines through the origin in $ \mathbf R ^ {n+1} $, respectively $ \mathbf C ^ {n+1} $, are the Grassmann manifolds $ G _ {n+1,1} ( \mathbf R ) = \mathop{\rm Gr} _ {1} ( \mathbf R ^ {n+1} ) $, $ G _ {n+1,1} ( \mathbf C ) = \mathop{\rm Gr} _ {1} ( \mathbf C ^ {n+1} ) $( cf. Grassmann manifold).
$ \mathbf P _ {n} ( \mathbf C ) $ has a CW-decomposition of exactly one cell $ e _ {2m} $ in each even dimension. Consequently, its homology is $ H _ {2i} ( \mathbf P _ {n} ( \mathbf C ) ; \mathbf Z ) = \mathbf Z $ for $ i = 0 \dots n $ and $ H _ {2i+1} ( \mathbf P _ {n} ( \mathbf C ) ; \mathbf Z ) = 0 $ for $ i = 0 \dots n- 1 $.
Real projective space has a CW-decomposition with exactly one cell in each dimension. For odd $ n = 2m + 1 $ the homology groups are: $ H _ {2i} ( \mathbf P _ {2m+1} ( \mathbf R ) ) = 0 $, $ i = 1 \dots m $, $ H _ {0} ( \mathbf P _ {2m+1} ( \mathbf R )) = \mathbf Z $; $ H _ {2m+1} ( \mathbf P _ {2m+1} ( \mathbf R )) = \mathbf Z $; $ H _ {2i+1} ( \mathbf P _ {2m+1} ( \mathbf R )) = \mathbf Z / ( 2) $ for $ i = 0 \dots m- 1 $. For even $ n = 2m $ the homology groups are: $ H _ {0} ( \mathbf P _ {2m} ( \mathbf R )) = \mathbf Z $; $ H _ {2i} ( \mathbf P _ {2m} ( \mathbf R )) = 0 $, $ i = 1 \dots m $; $ H _ {2i+1} ( \mathbf P _ {2m} ( \mathbf R )) = \mathbf Z / ( 2) $, $ i= 0 \dots m- 1 $.
The real projective plane can be obtained by glueing a disc along its boundary to the boundary of a crosscap (i.e. a Möbius strip). An easy way to see this is to view $ \mathbf P _ {2} ( \mathbf R ) $ as obtained from a disc by identifying diametrically-opposite boundary points. Now remove a central disc and cut and glue as indicated below.
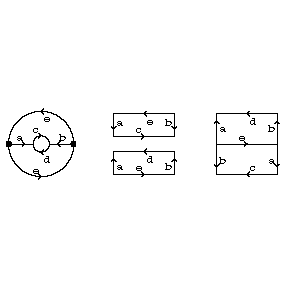
Figure: p075350a
The real projective plane cannot be imbedded in $ \mathbf R ^ {3} $, but can be imbedded in $ \mathbf R ^ {4} $. Its Euler characteristic is 1.
References
| [a1] | O. Veblen, J.W. Young, "Projective geometry" , 1–2 , Blaisdell (1938–1946) MR0179667 MR0179666 MR1519256 MR1506049 MR1500790 MR1500747 Zbl 0127.37604 Zbl 0018.32604 Zbl 63.0693.02 Zbl 55.0413.02 Zbl 52.0732.01 Zbl 51.0591.05 Zbl 51.0569.04 Zbl 49.0547.01 Zbl 48.0843.04 Zbl 47.0582.08 Zbl 41.0606.06 Zbl 39.0606.01 Zbl 38.0562.01 |
| [a2] | R. Baer, "Linear algebra and projective geometry" , Acad. Press (1952) MR0052795 Zbl 0049.38103 |
Projective space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Projective_space&oldid=55072