Projective set

A set that can be obtained from Borel sets (cf. Borel set) by repeated application of the operations of projection and taking complements. Projective sets are classified in classes forming the projective hierarchy. Let $ I = \omega ^ \omega $ be the Baire space (homeomorphic to the space of irrational numbers). A set $ P \subset I ^ {m} $ belongs to: 1) the class $ A _ {1} $ if $ P $ is the projection of a Borel set in the space $ I ^ {m+} 1 $; 2) the class $ CA _ {n} $( $ P $ is a $ CA _ {n} $- set) if its complement $ I ^ {m} \setminus P $ is an $ A _ {n} $- set $ ( n \geq 1 ) $; 3) the class $ A _ {n} $( $ P $ is an $ A _ {n} $- set) if $ P $ is the projection of a $ CA _ {n-} 1 $- set in the space $ I ^ {m+} 1 $, $ n \geq 2 $; and 4) the class $ B _ {n} $ if $ P $ belongs simultaneously to the classes $ A _ {n} $ and $ CA _ {n} $, $ n \geq 1 $. The same classes are obtained when the projection is replaced by a continuous image (of a set in the same space $ I ^ {m} $).

By virtue of the Suslin theorem, the class $ A _ {1} $ coincides with the class of $ {\mathcal A} $- sets (consequently, the class $ C A _ {1} $ coincides with the class of $ C {\mathcal A} $- sets, cf. $ {\mathcal A} $- set; $ C {\mathcal A} $- set), and the class $ B _ {1} $ coincides with the class of Borel sets. For every class $ A _ {n} $ a universal set is constructed and used to prove the following projective hierarchy theorem ( "existence" theorem, theorem on "non-emptiness of the classes" ): $ B _ {n} \subset A _ {n} \subset B _ {n+} 1 $( consequently, $ A _ {n} \subset B _ {n+} 1 \subset A _ {n+} 1 $), where each inclusion is strict. The cardinality of the set of all projective sets of the space $ I $ equals $ 2 ^ {\aleph _ {0} } $.

Every $ A _ {2} $- set is a union of $ \aleph _ {1} $ Borel sets and hence is either countable, or has cardinality $ \aleph _ {1} $ or $ 2 ^ {\aleph _ {0} } $( see [2] and [7] ). For the class $ A _ {2} $ the uniformization and reduction principles hold, while for the class $ CA _ {2} $ the (first) separation principle holds; cf. Descriptive set theory. Each projective class with index $ n \geq 2 $ is invariant under the $ {\mathcal A} $- operation. For each of the classes $ A _ {n} $, $ CA _ {n} $ there is a $ \delta $- $ \sigma $- operation that yields exactly all the sets of the class, starting from closed sets. The study of projective sets (even of the second class) is a difficult problem. Many problems in the theory of projective sets turned out to be undecidable in the classical sense, which completely confirmed the foresight (see [6]): "The field of projective sets is a field where the principle of the excluded middle is not strong enough any more" . The theory of projective sets was advanced further by involving strong set-theoretic assumptions, such as $ \mathop{\rm MC} $( there exists a measurable cardinal), $ \mathop{\rm PD} $( the projective determinacy axiom) and $ V = L $( the constructibility axiom, cf. Gödel constructive set).

Under the assumption $ \mathop{\rm MC} $: Every $ A _ {2} $- set is (Lebesgue-) measurable, has the Baire property and, if uncountable, contains a (non-empty) perfect subset; every $ A _ {3} $- set can be uniformized by an $ A _ {4} $- set.

Under the assumption $ \mathop{\rm PD} $: a) Every projective set is measurable, has the Baire property and, if uncountable, contains a perfect subset and can be uniformized by a projective set; more precisely, the uniformization principle holds for the classes $ A _ {2n} $ and $ CA _ {2n+} 1 $. b) For the classes $ A _ {2n} $ and $ CA _ {2n+} 1 $ the reduction principle holds, hence for the classes $ A _ {2n+} 1 $ and $ CA _ {2n} $ the separation principle holds.

Under the assumption $ V = L $: a) There exists an uncountable $ CA $- set that does not contain a perfect subset, and there exists a non-measurable $ B _ {2} $- set without the Baire property. b) For $ n \geq 2 $ the uniformization principle holds for the class $ A _ {n} $.

If for a class $ A _ {n} $ the uniformization principle holds, then so does the reduction principle. For $ n \geq 3 $ the reverse implication is unprovable in $ \mathop{\rm ZFC} $. If there exists a non-measurable $ A _ {2} $- set (or an $ A _ {2} $- set without the Baire property), then there exists an uncountable $ CA $- set that does not contain a perfect subset. If every uncountable $ CA $- set contains a perfect subset, then the same is true for every uncountable $ A _ {2} $- set (see [7]). The results mentioned here are true not only for the space $ I $ but also for the number axis and, in general, for any complete separable metric space. The following theorem on the topological invariance of projective sets is true: The homeomorphic image of a projective set of a given class situated in the same or in any other complete separable metric space is a projective set of the same class.

References

[1]	N.N. Lusin, "Sur les ensembles projectifs de M. Henri Lebesgue" C.R. Acad. Sci. Paris , 180 (1925) pp. 1572–1574
[2]	W. Sierpiński, "Sur une classe d'ensembles" Fund. Math. , 7 (1925) pp. 237–243
[3]	K. Kuratowski, "Topology" , 1 , PWN & Acad. Press (1966) (Translated from French)
[4]	K. Kuratowski, A. Mostowski, "Set theory" , North-Holland (1976) (Translated from Polish)
[5]	W. Sierpiński, "Les ensembles projectifs et analytiques" , Gauthier-Villars (1950)
[6]	N.N. Luzin, , Collected works , 2 , Moscow (1958) pp. 242; 268 (In Russian)
[7]	T.J. Jech, "Set theory" , Acad. Press (1978) (Translated from German)
[8]	P. Hinman, "Recursion-theoretic hierarchies" , Springer (1978)
[9]	P.S. Novikov, , Selected works , Moscow (1979) (In Russian)
[10]	Z.I. Kozlova, "On projective operations and the separability of projective sets" Izv. Akad. Nauk SSSR Ser. Mat. , 26 : 2 (1962) pp. 223–260 (In Russian)
[11]	L.V. Kantorovich, E.M. Livenson, Fund. Math. , 18 (1932) pp. 214–279
[12]	D.A. Martin, "Descriptive set theory: projective sets" J. Barwise (ed.) , Handbook of mathematical logic , North-Holland (1977) pp. 783–815
[13]	Y. Moschovakis, "New methods and results in descriptive set theory" R. James (ed.) , Proc. Internat. Congress Mathematicians (Vancouver, 1974) , 1 , Canad. Math. Congress (1975) pp. 251–257
[14]	V.G. Kanovei, "On some problems of descriptive set theory and the connection between constructability and definability" Soviet Math. Dokl. , 22 : 1 (1980) pp. 163–167 Dokl. Akad. Nauk SSSR , 253 : 4 (1980) pp. 800–803
[15]	V.A. Lyubetskii, "Random sequences of numbers, and -sets" , Studies in Set Theory and Non-Classical Logics , Moscow (1976) pp. 96–122 (In Russian)
[16]	A. Kechris, "On transfinite sequences of projective sets with an application to 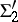equivalence relations" , Logic colloquium '77 , Studies in logic and foundations of math. , 96 , North-Holland (1978) pp. 155–160
[17]	R. Mauldin, "Non-isomorphic projective sets" Mathematika , 23 : 2 (1976) pp. 151–155
[18]	S. Marcus, "Hamelsche Basis und projective Mengen" Math. Nachr. , 17 : 3–6 (1959) pp. 143–150
[19]	Z.I. Kozlova, V.P. Filippov, "Classes of projective sets in certain topological spaces of uncountable weight II" Soviet Math. Izv. Vuz. , 22 : 7 (1978) pp. 27–31 Izv. Vyzov. Mat. , 7 (1978) pp. 33–39

Comments

A more common notation for the projective classes is as follows: One writes

$ \Sigma _ \sim {} _ {n} ^ {1} $ for the class of $ A _ {n} $- sets,

$ \Pi _ \sim {} _ {n} ^ {1} $ for the class of $ CA _ {n} $- sets, and

$ \Delta _ \sim {} _ {n} ^ {1} $ for the class of $ B _ {n} $- sets.

This notation reflects the way one can describe these sets: a $ \Sigma _ \sim {} _ {n} ^ {1} $- set can be described by a formula which (in its normal formal) has $ n $ alternating quantifiers, starting with $ \exists $; likewise, the description of a $ \Pi _ \sim {} _ {n} ^ {1} $- set has $ n $ alternating quantifiers, starting with $ \forall $.

See also Descriptive set theory, especially .