Projective algebra

in the narrow sense

An algebra of points on a projective line; projectively-invariant constructions for defining addition and multiplication of points on a projective line $ l $, lying in a projective plane $ \pi $ for which the Desargues assumption holds. These constructions depend on the choice of three distinct points $ O, E, U $ on $ l $.

Construction I

determines for any two points $ A, B $ different from $ U $ a third point $ A + B $, also different from $ U $ and called the sum of $ A $ and $ B $. One draws in $ \pi $ three straight lines $ a $, $ b $ and $ u $, different from $ l $, forming a triangle and passing through $ A $, $ B $ and $ U $, respectively. Let $ P $ be the point of intersection of $ u $ and $ a $, let $ Q $ be that of $ u $ and $ b $, $ R $ that of $ OQ $ and $ a $, and $ S $ that of $ b $ and $ UR $. Then $ PS $ intersects $ l $ in the point $ T = A + B $( for the general case see Fig. a). It turns out that the point thus constructed depends on $ A $, $ B $, $ O $, and $ U $ only, and not on the choice of the straight lines or the point $ E $.

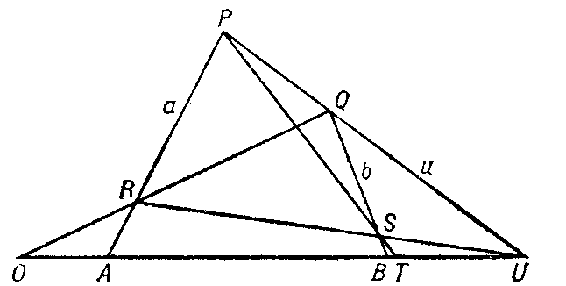
Figure: p075160a

Construction II

determines for any two points $ A, B $ different from $ U $ a third point $ A \cdot B $, also different from $ U $ and called the product of $ A $ and $ B $. One draws in $ \pi $ three straight lines $ a $, $ b $ and $ u $, different from $ l $, forming a triangle and passing through $ A $, $ B $ and $ U $, respectively. Let $ P $ be the point of intersection of $ u $ and $ a $, let $ Q $ be that of $ u $ and $ b $, $ R $ that of $ EQ $ and $ a $, and $ S $ that of $ OR $ and $ b $. Then $ PS $ intersects $ l $ in the point $ T = A \cdot B $( for the general case see Fig. b). It turns out that the point thus constructed depends on $ A $, $ B $, $ O $, $ E $, $ U $ only, and not on the choice of the straight lines $ a $, $ b $ and $ u $. The points of the line $ l $( distinct from $ U $) form a skew-field $ K ( O, E, U) $ under these operations of addition and multiplication. Interchanging $ A $ and $ B $ in construction II leads to an anti-isomorphic skew-field $ K ^ {*} ( O, E, U) $. If $ O _ {1} , E _ {1} , U _ {1} $ is another triple of points on a straight line $ l _ {1} $ in $ \pi $, then the corresponding skew-field $ K _ {1} ( O _ {1} , E _ {1} , U _ {1} ) $ is isomorphic to $ K ( O, E, U) $, since there is a projective correspondence between $ l $ and $ l _ {1} $. Therefore, any skew-field isomorphic to it is simply called a skew-field of the given projective plane (or even of the given projective geometry). One also says that one has a projective geometry over the skew-field $ K $. In the general cases of constructions I and II there figure four points $ P $, $ Q $, $ R $, $ S $, lying in one plane and no three of which are collinear; these form a complete quadrangle with three pairs of opposite sides $ PQ $, $ RS $; $ PS $, $ QR $; and $ PR $, $ QS $. The points $ X, Y, Z $ of intersection of these pairs of opposite sides are called diagonal points, while the straight lines joining diagonal points are called diagonals. A special case, not indicated in the figure, corresponds to the situation that $ X, Y, Z $ are collinear (see Fano postulate).

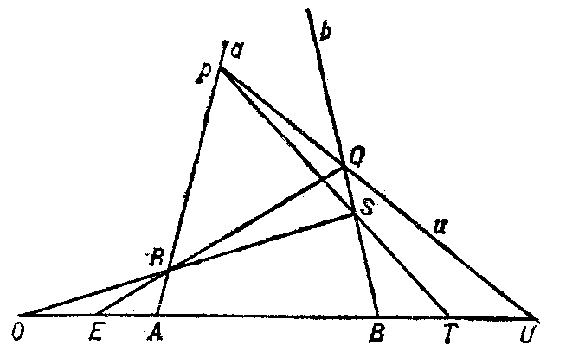
Figure: p075160b

Similar constructions can be carried out in a pencil of straight lines passing through a point, using a complete quadrilateral, a figure dual to a quadrangle, and leading to a skew-field $ K ^ {*} $ anti-isomorphic to $ K $.

The properties of the projective line $ l $ as an algebraic system are determined by the geometric (projectively-invariant) properties of the projective plane in which $ l $ lies. E.g., commutativity of $ K $ is equivalent to the Pappus axiom being true; Fano's postulate is equivalent to the characteristic of $ K $ being different from 2; if $ K $ has no other automorphisms but inner ones, then every projective transformation is a collineation, etc.

Using the skew-field $ K $ on the straight line, and hence in the projective space containing the line, one can introduce projective coordinates, giving an algebraic model of the projective space, so that the contents of the projective geometry is, in essence, determined by properties of the same skew-field $ K $ over which it is constructed.

In the wide sense, in projective geometry one studies the set of subspaces of projective space, which is a complemented modular lattice. Here one does not require the space to be finite-dimensional, but imposes the condition of completeness, existence of a homogeneous basis, etc. Accordingly, one can establish various connections with the theory of prime and regular rings, the theory of Abelian operator groups and other branches of algebra.

References

[1]	W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , 1 , Cambridge Univ. Press (1947) MR0028055 Zbl 0796.14002 Zbl 0796.14003 Zbl 0796.14001 Zbl 0157.27502 Zbl 0157.27501 Zbl 0055.38705 Zbl 0048.14502
[2]	E. Artin, "Geometric algebra" , Interscience (1957) MR1529733 MR0082463 Zbl 0077.02101

Comments

A collineation is a linear transformation of the homogeneous coordinates (Baer's terminology, [a2]).

The construction of projective geometry using the properties of its skew-field is rather old; it is essentially due to D. Hilbert [a1]. A modern approach was given by E. Artin [2].

References

[a1]	D. Hilbert, "Grundlagen der Geometrie" , Teubner, reprint (1968) MR0262046 MR0229120 Zbl 0153.49601
[a2]	R. Baer, "Linear algebra and projective geometry" , Acad. Press (1952) MR0052795 Zbl 0049.38103
[a3]	H.S.M. Coxeter, "The real projective plane" , Cambridge Univ. Press (1961) MR1198272 MR1198271 MR0112071 MR0124786 MR0070189 MR1570447 MR0030205 Zbl 0772.51001 Zbl 0086.35805 Zbl 0090.12104 Zbl 0065.36401 Zbl 0032.11302