Product integral

A limit of products of the form

$$ \prod _ \Delta = \ e ^ {A ( s _ {n} ) ( s _ {n} - s _ {n-1} ) } e ^ {A ( s _ {n-1} ) ( s _ {n-1} - s _ {n-2} ) } {} \dots e ^ {A ( s _ {1} ) ( s _ {1} - s _ {0} ) } , $$

where $ A $ is a continuous function on $ [ a , b ] $ with values in the space of bounded operators on a Banach space $ E $ and $ \Delta $ is the partition of $ [ a , b ] $ by points $ s _ {0} = a , s _ {1}, \dots, s _ {n} = b $. The limit is taken as the diameter of the partition $ | \Delta | \rightarrow 0 $ and is denoted by

$$ {\int\limits _ { a } ^ { \tilde{b } } } \mathop{\rm exp} A( s) d s . $$

If the operators $ A ( t) $ commute for different $ t $, then

$$ {\int\limits _ { a } ^ { \tilde{b } } } \mathop{\rm exp} A ( s) d s = \ e ^ {\int\limits _ {a} ^ {b} A ( s) d s } . $$

A product integral is a convenient way of representing an evolution operator $ U ( t , \tau ) $ for a differential equation $ \dot{X} = A ( t) X $ (see [1]). Here

$$ \tag{1 } U ( t , \tau ) = \ {\int\limits _ \tau ^ { \tilde t } } \mathop{\rm exp} A ( s) d s . $$

The products whose limit is the latter integral are also the evolution operators for the equations with piecewise-constant operators $ \widetilde{A} ( t) = A ( s _ {k} ) $ for $ s _ {k-1} \leq t \leq s _ {k} $.

If $ A $ and $ B $ are two continuous operator-valued functions, then

$$ \tag{2 } {\int\limits _ { a } ^ { \tilde b } } \mathop{\rm exp} ( A ( s) + B ( s) ) d s = $$

$$ = \ \lim\limits _ {| \Delta | \rightarrow 0 } {\prod _ { k= 1} ^ { \tilde{n } } } e ^ {A ( s _ {k} ) ( s _ {k} - s _ {k-1} ) } e ^ {B ( s _ {k} ) ( s _ {k} - s _ {k-1} ) } , $$

where the sign $ \widetilde{ {}} $ over the product means that the factors with low indices are written to the right of the factors with high indices.

Formulas (1) and (2) can be generalized to certain classes of differential equations with unbounded operator functions, from which representations of the solutions of parabolic and Schrödinger-type partial differential equations in the form of integrals over the space of trajectories (path integrals, continual integrals, cf. Integral over trajectories) are obtained (see [2]).

Formulas of the type (2) are at the basis of certain numerical methods for solving equations.

If $ f $ is a scalar-valued continuous function and $ F $ is an operator-valued function of bounded variation, then the limit

$$ \lim\limits _ {| \Delta | \rightarrow 0 } \ {\prod _ { k= 1} ^ { \tilde{n } } } e ^ {f ( s _ {k} ) ( F ( s _ {k} ) - F ( s _ {k-1} ) ) } = \ {\int\limits _ { a } ^ { \tilde{b } } } \mathop{\rm exp} ( f ( t) d F ( t) ) $$

exists; it is called the product Stieltjes integral. These integrals have been applied in the theory of $ J $-contracting matrices and operators (see [3], [4]).

References

[1]	Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian)
[2]	Yu.L. Daletskii, "Functional integrals connected with operator evolution equations" Russian Math. Surveys , 17 : 5 (1962) pp. 1–107 Uspekhi Mat. Nauk , 17 : 5 (1962) pp. 3–115
[3]	V.P. Potapov, "The multiplicative structure of 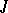-contractive matrix functions" Trudy Moskov. Mat. Obshch. , 4 (1955) pp. 125–236 (In Russian)
[4]	Yu.P. Ginzburg, "Multiplicative representations of 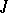-contractive operator functions I" Mat. Issled. (Kishinev) , 2 : 2 (1967) pp. 52–83 (In Russian)

References

[a1]	M. Reed, B. Simon, "Methods of modern mathematical physics" , 2 , Acad. Press (1972)
[a2]	J.D. Dollard, Ch.N. Friedman, "Product integration" , Addison-Wesley (1979)