Porosity point
of a set $ E $
in a metric space $ X $
A point $ x _ {0} \in X $ for which there exists a sequence of open balls $ B _ {k} $ with radii $ r _ {k} \rightarrow 0 $ and common centre at the point $ x _ {0} $, such that for any $ k = 1 , 2 \dots $ there is an open ball $ G _ {k} \subset B _ {k} \setminus E $ with radius $ \rho _ {k} \geq C r _ {k} $, where $ C $ is positive and independent of $ k $( but, generally speaking, depends on $ x _ {0} $ and $ E $). A set $ E $ is called porous if any point in it is a porosity point of it. A set $ E $ is called $ \sigma $- porous if it can be represented as a finite or countable union of porous sets (see [1]). A porosity point of $ E $ is a porosity point of its closure $ \overline{E}\; $. If $ X = \mathbf R ^ {n} $, a porosity point of a set $ E \subset X $ is not a Lebesgue density point either of $ E $ or of $ \overline{E}\; $. Any porous or $ \sigma $- porous set $ E \subset \mathbf R ^ {n} $ is of the first Baire category (cf. Baire classes) and of Lebesgue measure zero in $ \mathbf R ^ {n} $. The converse of this statement, generally speaking, does not hold: There even exist nowhere-dense perfect sets $ E \subset \mathbf R ^ {1} $ of measure zero that are not $ \sigma $- porous (see [2]).
Sometimes, in the case of an infinite-dimensional space $ X $, porous and $ \sigma $- porous sets take the role of sets of measure zero. If $ X = \mathbf R ^ {n} $ and $ h: [ 0, \infty ) \rightarrow \mathbf R $ is an increasing continuous function with $ h( 0) = 0 $, then $ x _ {0} \in X $ is called an $ h $- porous point of a set $ E \subset X $ if $ h ( \rho _ {k} ) \geq Cr _ {k} $, using the same notations ( $ C $ is independent of $ k $). The concepts of $ h $- porous and $ \sigma $- $ h $- porous sets are defined accordingly. In the case $ h( t)/t \rightarrow \infty $( $ t \rightarrow 0 $), a $ h $- porous set $ E \subset X = \mathbf R ^ {n} $ may be a set of positive Lebesgue measure.
References
| [1] | E.P. Dolzhenko, "Boundary properties of arbitrary functions" Math. USSR Izv. , 1 : 1 (1967) pp. 1–12 Izv. Akad. Nauk. SSSR Ser. Mat. , 31 : 1 (1967) pp. 3–14 |
| [2] | L. Zajiček, "Sets of 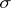 -porosity and sets of -porosity and sets of 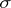 -porosity -porosity 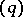 " Casopis. Pešt. Mat. , 101 (1976) pp. 350–359 " Casopis. Pešt. Mat. , 101 (1976) pp. 350–359 |
| [3] | J. Foran, P.D. Humke, "Some set-theoretic properties of 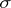 -porous sets" Real Anal. Exch. , 6 : 1 (1980/81) pp. 114–119 -porous sets" Real Anal. Exch. , 6 : 1 (1980/81) pp. 114–119 |
| [4] | J. Tkadlec, "Constructions of some non-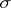 - -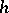 -porous sets on the real line" Real Anal. Exch. , 9 : 2 (1983/84) pp. 473–482 -porous sets on the real line" Real Anal. Exch. , 9 : 2 (1983/84) pp. 473–482 |
| [5] | S.J. Agronsky, A.M. Bruckner, "Local compactness and porosity in metric spaces" Real Anal. Exch. , 11 : 2 (1985/86) pp. 365–379 |
| [6] | Yu.A. Shevchenko, "On Vitali's covering theorem" Vestnik Moskov. Univ. Ser. 1. Mat. Mech. : 3 (1989) pp. 11–14 (In Russian) |
Porosity point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Porosity_point&oldid=48246