Polynomial convexity
Let $\mathcal{P}$ denote the set of holomorphic polynomials on $\mathbf{C} ^ { n }$ (cf. also Analytic function). Let $K$ be a compact set in $\mathbf{C} ^ { n }$ and let $\| P \| _ { K } = \operatorname { max } _ { z \in K } | P ( z ) |$ be the sup-norm of $P \in \mathcal{P}$ on $K$. The set
\begin{equation*} \hat { K } = \{ z \in {\bf C} ^ { n } : | P ( z ) | \leq \| P \| _ { K } , \forall P \in {\cal P} \}, \end{equation*}
is called the polynomially convex hull of $K$. If $\hat { K } = K$ one says that $K$ is polynomially convex.
An up-to-date (as of 1998) text dealing with polynomial convexity is [a3], while [a13] and [a27] contain some sections on polynomial convexity, background and older results. The paper [a24] is an early study on polynomial convexity.
Polynomial convexity arises naturally in the context of function algebras (cf. also Algebra of functions): Let $P ( K )$ denote the uniform algebra generated by the holomorphic polynomials on $K$ with the sup-norm. The maximal ideal space $M$ of $P ( K )$ is the set of homomorphisms mapping $P ( K )$ onto $\mathbf{C}$, endowed with the topology inherited from the dual space $P ( K ) ^ { * }$. It can be identified with 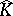 via
via
\begin{equation*} z \in \widehat { K } \leftrightarrow m _ { z }, \end{equation*}
\begin{equation*} P \mapsto P ( z ) , P \in \mathcal{P}. \end{equation*}
Moreover, if $A$ is any finitely generated function algebra on a compact Hausdorff space, then $A$ is isomorphic to $P ( K )$, where for $K$ one can take the joint spectrum of the generators of $A$ (cf. also Spectrum of an operator).
By the Riesz representation theorem (cf. Riesz theorem) there exists for every $z \in \hat { K }$ at least one representing measure $\mu _ { z }$, that is, a probability measure $\mu _ { z }$ on $K$ such that
\begin{equation*} P ( z ) = m _ { z } ( P ) = \int _ { K } P ( \zeta ) d \mu _ { z } ( \zeta ) , P \in \mathcal{P}. \end{equation*}
One calls $\mu _ { z }$ a Jensen measure if it has the stronger property
\begin{equation*} \operatorname { log } | P ( z ) | \leq \int _ { K } \operatorname { log } | P ( \zeta ) | d \mu _ { z } ( \zeta ) , P \in \mathcal{P}. \end{equation*}
It can be shown that for each $z \in \hat { K }$ there exists a Jensen measure $\mu _ { z }$. See e.g. [a27].
For compact sets $K$ in $\mathbf{C}$ one obtains 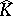 by "filling in the holes" of $K$, that is, $\hat { K } = \mathbf{C} \backslash \Omega _ { \infty }$, where $\Omega _ { \infty }$ is the unbounded component of $\mathbf{C} \backslash K$. In $\mathbf{C} ^ { n }$, $n > 1$, there is no such a simple topological description.
by "filling in the holes" of $K$, that is, $\hat { K } = \mathbf{C} \backslash \Omega _ { \infty }$, where $\Omega _ { \infty }$ is the unbounded component of $\mathbf{C} \backslash K$. In $\mathbf{C} ^ { n }$, $n > 1$, there is no such a simple topological description.
Early results on polynomial convexity, cf. [a13], are
Oka's theorem: If $K$ is a polynomially convex set in $\mathbf{C} ^ { n }$ and $f$ is holomorphic on a neighbourhood of $K$, then $f$ can be written on $K$ as a uniform limit of polynomials. Cf. also Oka theorems.
Browder's theorem: If $K$ is polynomially convex in $\mathbf{C} ^ { n }$, then $H ^ { p } ( K , {\bf C} ) = 0$ for $p \geq n$.
Here, $H ^ { p } ( K , \mathbf{C} )$ is the $p$th Čech cohomology group. More recently (1994), the following topological result was obtained, cf. [a9], [a3]:
Forstnerič' theorem: Let $K$ be a polynomially convex set in $\mathbf{C} ^ { n }$, $n \geq 2$. Then
\begin{equation*} H _ { k } ( \mathbf{C} ^ { n } \backslash K ; G ) = 0,1 \leq k \leq n - 1, \end{equation*}
and
\begin{equation*} \pi _ { k } ( \mathbf{C} ^ { n } \backslash K ) = 0,1 \leq k \leq n - 1. \end{equation*}
Here, $H _ { k } ( X , G )$ denotes the $k$th homology group of $X$ with coefficients in an Abelian group $G$ and $\pi _ { k } ( X )$ is the $k$th homotopy group of $X$.
One method to find 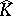 is by means of analytic discs. Let $\Delta$ be the unit disc in $\mathbf{C}$ and let $T$ be its boundary. An analytic disc is (the image of) a holomorphic mapping $f : \Delta \rightarrow {\bf C} ^ { n }$ such that $f$ is continuous up to $T$. Similarly one defines an $H ^ { \infty }$-disc as a bounded holomorphic mapping $f : \Delta \rightarrow {\bf C} ^ { n }$. Its components are elements of the usual Hardy space $H ^ { \infty } ( \Delta )$ (cf. Hardy spaces).
is by means of analytic discs. Let $\Delta$ be the unit disc in $\mathbf{C}$ and let $T$ be its boundary. An analytic disc is (the image of) a holomorphic mapping $f : \Delta \rightarrow {\bf C} ^ { n }$ such that $f$ is continuous up to $T$. Similarly one defines an $H ^ { \infty }$-disc as a bounded holomorphic mapping $f : \Delta \rightarrow {\bf C} ^ { n }$. Its components are elements of the usual Hardy space $H ^ { \infty } ( \Delta )$ (cf. Hardy spaces).
Now, let $K$ be compact in $\mathbf{C} ^ { n }$ and suppose that $f ( T ) \subset K$ for some analytic disc $f$. Then $f ( \Delta ) \subset \hat { K }$ by the maximum principle applied to $P \circ f$ for polynomials $P \in \mathcal{P}$. The same goes for $H ^ { \infty }$-discs whose boundary values are almost everywhere in $K$. One says that the disc $f$ is glued to $K$. Next, one says that 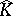 has analytic structure at $p \in \hat{K}$ if there exists a non-constant analytic disc $f$ such that $f ( 0 ) = p$ and the image of $f$ is contained in
has analytic structure at $p \in \hat{K}$ if there exists a non-constant analytic disc $f$ such that $f ( 0 ) = p$ and the image of $f$ is contained in 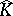 .
.
It was a major question whether $\hat{K} \backslash K$ always has analytic structure. Moreover, when is 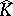 obtained by glueing discs to $K$? One positive result in this direction is due to H. Alexander [a1]; a corollary of his work is as follows: If $K$ is a rectifiable curve in $\mathbf{C} ^ { n }$, then either $\hat { K } = K$ and $P ( K ) = C ( K )$, or $\hat{K} \backslash K$ is a pure $1$-dimensional analytic subset of $\mathbf{C} ^ { n } \backslash K$ (cf. also Analytic set). If $K$ is a rectifiable arc, $K$ is polynomially convex and $P ( K ) = C ( K )$.
obtained by glueing discs to $K$? One positive result in this direction is due to H. Alexander [a1]; a corollary of his work is as follows: If $K$ is a rectifiable curve in $\mathbf{C} ^ { n }$, then either $\hat { K } = K$ and $P ( K ) = C ( K )$, or $\hat{K} \backslash K$ is a pure $1$-dimensional analytic subset of $\mathbf{C} ^ { n } \backslash K$ (cf. also Analytic set). If $K$ is a rectifiable arc, $K$ is polynomially convex and $P ( K ) = C ( K )$.
See [a1] for the complete formulation. Alexander's result is an extension of pioneering work of J. Wermer, cf. [a30], E. Bishop and, later, G. Stolzenberg [a26], who dealt with real-analytic, respectively $C ^ { 1 }$, curves. Wermer [a29] gave the first example of an arc in $\mathbf{C} ^ { 3 }$ that is not polynomially convex, cf. [a3]. However, Gel'fand's problem (i.e., let $\gamma$ be an arc in $\mathbf{C} ^ { n }$ such that $\hat{\gamma} = \gamma$; is it true that $P ( \gamma ) = C ( \gamma )$?) is still open (2000). Under the additional assumption that its projections into the complex coordinate planes have $2$-dimensional Hausdorff measure $0$, the answer is positive, see [a3].
F.R. Harvey and H.B. Lawson gave a generalization to higher-dimensional $K$, cf. [a12], which includes the following.
Let $p \geq 1$. If $K$ is a $C ^ { 2 }$ $( 2 p + 1 )$-dimensional submanifold of $\mathbf{C} ^ { n }$ and at each point of $K$ the tangent space to $K$ contains a $p$-dimensional complex subspace, then $K$ is the boundary of an analytic variety (in the sense of Stokes' theorem).
Another positive result is contained in the work of E. Bedford and W. Klingenberg, cf. [a4]: Suppose $\Gamma \subset {\bf C} ^ { 2 }$ is the graph of a $C ^ { 2 }$-function $\phi$ over the boundary of a strictly convex domain $\Omega \subset \mathbf{C} \times \mathbf{R}$. Then $\widehat{\Gamma}$ is the graph of a Lipschitz-continuous extension $\Phi$ of $\phi$ on $\Omega$. Moreover, $\widehat{\Gamma}$ is foliated with analytic discs (cf. also Foliation).
The work of Bedford and Klingenberg has been generalized in various directions in [a16], [a21] and [a7]. One ingredient of this theorem is work of Bishop [a5], which gives conditions that guarantee locally the existence of analytic discs with boundary in real submanifolds of sufficiently high dimension. See [a11], [a32] and [a15] for results along this line.
A third situation that is fairly well understood is when $K \subset \mathbf{C} ^ { n + 1 }$ is a compact set fibred over $T$, that is, $K$ is of the form $K = \{ ( z , w ) : z \in T , w \in K _ { z } \}$, where $K _ { z }$ is a compact set in $\mathbf{C} ^ { n }$ depending on $z$.
In this case the following is true: Let $K \subset \mathbf{C} ^ { 2 }$ be a compact fibration over the circle $T$ and suppose that for each $z$ the fibre $K _ { z }$ is connected and simply connected. Then $\hat{K} \backslash K$ is the union of graphs $\Gamma _ { f }$, where $f \in H ^ { \infty } ( \Delta )$ and the boundary values $f ^ { * } ( z )$ are in $K _ { z }$ for almost all $z \in T$.
Of course, it is possible that $\hat{K} \backslash K$ is empty. The present theorem is due to Z. Slodkowski, [a22], earlier results are in [a2] and [a10]. Slodkowski proved a similar theorem in $\mathbf{C} ^ { n + 1}$ under the assumption that the fibres are convex, see [a23].
Despite these positive results, in general $\hat{K} \backslash K$ need not have analytic structure. This has become clear from examples by Stolzenberg [a25] and Wermer [a31]. Presently (2000) it is not known whether 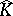 has analytic structure everywhere if $K$ is a (real) submanifold of $\mathbf{C} ^ { n }$, nor is it known under what conditions
has analytic structure everywhere if $K$ is a (real) submanifold of $\mathbf{C} ^ { n }$, nor is it known under what conditions 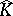 is obtained by glueing discs to $K$.
is obtained by glueing discs to $K$.
However, it has been shown that in a weaker sense there is always a kind of analytic structure in polynomial hulls. Let $d \theta$ denote Lebesgue measure on the circle $T$ and let $f ^ { * } d \theta$ denote the push-forward of $d \theta$ under a continuous mapping $f : T \rightarrow \mathbf{C} ^ { n }$. Let also $K$ be a compact set in $\mathbf{C} ^ { n }$. The following are equivalent:
1) $z \in \hat { K }$ and $\mu _ { z }$ is a Jensen measure for $z$ supported on $K$;
2) There exists a sequence of analytic discs $f _ { j } : \Delta \rightarrow \mathbf{C} ^ { n }$ such that $f _ { j } ( 0 ) \rightarrow z$ and $f _ { j } ^ { * } d \theta / 2 \pi \rightarrow \mu _ { z }$ in the weak-$*$ sense (cf. also Weak topology).
This was proved in [a6]; [a8] and [a20] contain more information about additional nice properties that can be required from the sequence of analytic discs. Under suitable regularity conditions on $K$, it is shown in [a19] that  consists of analytic discs $f$ such that $f ^ { - 1 } ( K ) \cap T$ has Lebesgue measure arbitrary close to $2 \pi$.
consists of analytic discs $f$ such that $f ^ { - 1 } ( K ) \cap T$ has Lebesgue measure arbitrary close to $2 \pi$.
Another problem is to describe $P ( K )$ assuming that $K = \hat { K }$ and given reasonable additional conditions on $K$. In particular, when can one conclude that $P ( K ) = C ( K )$? Recall that a real submanifold $M$ of $\mathbf{C} ^ { n }$ is totally real at $p \in M$ if the tangent space in $p$ does not contain a complex line (cf. also CR-submanifold). The Hörmander–Wermer theorem is as follows, cf. [a14]: Let $M$ be a sufficiently smooth real submanifold of $\mathbf{C} ^ { n }$ and let $K _ { 0 }$ be the subset of $M$ consisting of points that are not totally real. If $K \subset M$ is a compact polynomially convex set that contains an $M$-neighbourhood of $K _ { 0 }$, then $P ( K )$ contains all continuous functions on $K$ that are on $K _ { 0 }$ the uniform limit of functions holomorphic in a neighbourhood of $K _ { 0 }$.
See [a17] for a variation on this theme. One can deal with some situations where the manifold is replaced by a union of manifolds; e.g., B.M. Weinstock [a28] gives necessary and sufficient conditions for any compact subset of the union of two totally real $n$-dimensional subspaces of $\mathbf{C} ^ { n }$ to be polynomially convex; then also $P ( K ) = C ( K )$. See also [a18].
References
| [a1] | H. Alexander, "Polynomial approximation and hulls in sets of finite linear measure in $\mathbf{C} ^ { n }$" Amer J. Math. , 62 (1971) pp. 65–74 MR0284617 Zbl 0221.32011 |
| [a2] | H. Alexander, J. Wermer, "Polynomial hulls with convex fibres" Math. Ann. , 281 (1988) pp. 13–22 |
| [a3] | H. Alexander, J. Wermer, "Several complex variables and Banach algebras" , Springer (1998) MR1482798 Zbl 0894.46037 |
| [a4] | E. Bedford, W. Klingenberg Jr., "On the envelope of holomorphy of a $2$-sphere in $\mathbf{C} ^ { 2 }$" J. Amer. Math. Soc. , 4 (1991) pp. 623–646 MR1094437 |
| [a5] | E. Bishop, "Differentiable manifolds in Euclidean space" Duke Math. J. , 32 (1965) pp. 1–21 MR200476 Zbl 0154.08501 |
| [a6] | S. Bu, W. Schachermayer, "Approximation of Jensen measures by image measures under holomorphic functions and applications" Trans. Amer. Math. Soc. , 331 (1992) pp. 585–608 MR1035999 Zbl 0758.46014 |
| [a7] | E.M. Chirka, N.V. Shcherbina, "Pseudoconvexity of rigid domains and foliations of hulls of graphs" Ann. Scuola Norm. Sup. Pisa , 22 (1995) pp. 707–735 MR1375316 Zbl 0868.32020 |
| [a8] | J. Duval, N. Sibony, "Polynomial convexity, rational convexity and currents" Duke Math. J. , 79 (1995) pp. 487–513 MR1344768 Zbl 0838.32006 |
| [a9] | F. Forstnerič, "Complements of Runge domains and holomorphic hulls" Michigan Math. J. , 41 (1994) pp. 297–308 MR1278436 Zbl 0811.32007 |
| [a10] | F. Forstnerič, "Polynomial hulls of sets fibered over the circle" Indiana Univ. Math. J. , 37 (1988) pp. 869–889 MR0982834 Zbl 0647.32017 |
| [a11] | F. Forstnerič, E.L. Stout, "A new class of polynomially convex sets" Ark. Mat. , 29 (1991) pp. 51–62 MR1115074 Zbl 0734.32006 |
| [a12] | F.R. Harvey, H.B. Lawson Jr., "On boundaries of complex analytic varieties I" Ann. of Math. , 102 (1975) pp. 223–290 MR0425173 Zbl 0317.32017 |
| [a13] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) MR0344507 Zbl 0271.32001 |
| [a14] | L. Hörmander, J. Wermer, "Uniform approximation on compact sets in $\mathbf{C} ^ { n }$" Math. Scand. , 23 (1968) pp. 5–21 MR0254275 Zbl 0181.36201 |
| [a15] | B. Jöricke, "Local polynomial hulls of discs near isolated parabolic points" Indiana Univ. Math. J. , 46 : 3 (1997) pp. 789–826 MR1488338 Zbl 0901.32010 |
| [a16] | N.G. Kruzhilin, "Two-dimensional spheres in the boundaries of strictly pseudoconvex domains in $\mathbf{C} ^ { 2 }$" Math. USSR Izv. , 39 (1992) pp. 1151–1187 (In Russian) MR1152210 Zbl 0778.32003 |
| [a17] | A.G. O'Farrell, K.J. Preskenis, D. Walsh, "Holomorphic approximation in Lipschitz norms" , Proc. Conf. Banach Algebras and Several Complex Variables (New Haven, Conn., 1983) , Contemp. Math. , 32 (1983) pp. 187–194 MR0769507 Zbl 0553.32015 |
| [a18] | P.J. de Paepe, "Approximation on a disk I" Math. Z. , 212 (1993) pp. 145–152 Zbl 0789.30027 |
| [a19] | E.A. Poletsky, "Holomorphic currents" Indiana Univ. Math. J. , 42 (1993) pp. 85–144 MR1218708 Zbl 0811.32010 |
| [a20] | E.A. Poletsky, "Analytic geometry on compacta in $\mathbf{C} ^ { n }$" Math. Z. , 222 (1996) pp. 407–424 MR1400200 Zbl 0849.32009 |
| [a21] | N. Shcherbina, "On the polynomial hull of a graph" Indiana Univ. Math. J. , 42 (1993) pp. 477–503 MR1237056 Zbl 0798.32026 |
| [a22] | Z. Slodkowski, "Polynomial hulls with convex convex sections and interpolating spaces" Proc. Amer. Math. Soc. , 96 (1986) pp. 255–260 MR818455 Zbl 0588.32017 |
| [a23] | Z. Slodkowski, "Polynomial hulls in $\mathbf{C} ^ { 2 }$ and quasi circles" Ann. Scuola Norm. Sup. Pisa , 16 (1989) pp. 367–391 MR1050332 |
| [a24] | G. Stolzenberg, "Polynomially and rationally convex sets" Acta Math. , 109 (1963) pp. 259–289 MR0146407 Zbl 0122.08404 |
| [a25] | G. Stolzenberg, "A hull with no analytic structure" J. Math. Mech. , 12 (1963) pp. 103–112 MR0143061 Zbl 0113.29101 |
| [a26] | G. Stolzenberg, "Uniform approximation on smooth curves" Acta Math. , 115 (1966) pp. 185–198 MR0192080 Zbl 0143.30005 |
| [a27] | E.L. Stout, "The theory of uniform algebras" , Bogden and Quigley (1971) MR0423083 Zbl 0286.46049 |
| [a28] | B.M. Weinstock, "On the polynomial convexity of the union of two maximal totally real subspaces of $\mathbf{C} ^ { n }$" Math. Ann. , 282 (1988) pp. 131–138 MR0960837 Zbl 0628.32015 |
| [a29] | J. Wermer, "Polynomial approximation on an arc in $\mathbf{C} ^ { 3 }$" Ann. of Math. , 62 (1955) pp. 269–270 MR0072260 Zbl 0067.05001 |
| [a30] | J. Wermer, "The hull of a curve in $\mathbf{C} ^ { n }$" Ann. of Math. , 68 (1958) pp. 550–561 MR0100102 Zbl 0084.33402 |
| [a31] | J. Wermer, "On an example of Stolzenberg" , Symp. Several Complex Variables, Park City, Utah , Lecture Notes in Mathematics , 184 , Springer (1970) MR0298428 |
| [a32] | J. Wiegerinck, "Local polynomially convex hulls at degenerated CR singularities of surfaces in $\mathbf{C} ^ { 2 }$" Indiana Univ. Math. J. , 44 (1995) pp. 897–915 MR1375355 Zbl 0847.32013 |
Polynomial convexity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polynomial_convexity&oldid=56253