Polynomial and exponential growth in groups and algebras

Let $ S ^ \prime = \{ g _ {1} \dots g _ {n} \} $ be a set of generators for a finitely-generated group $ G $. Consider $ S = \{ g _ {1} \dots g _ {n} , g _ {1} ^ {-1} \dots g _ {n} ^ {-1} \} $. Let $ S ^ {(n)} $ be the collection of all elements of $ G $ which can be written as a word in $ S $ of length $ \leq n $, and let $ f _ {G} ( n) = \# S ^ {(n)} $ be the number of elements of $ S ^ {(n)} $. The function $ f _ {G} ( n) $ is called the growth function of $ G $( with respect to the chosen generators). A similar definition can be given for algebras, cf. below. The subject of growth functions for algebras and groups studies the order of growth of functions like $ f _ {G} ( n) $ and relates this to group-theoretic properties of $ G $.

Consider a non-negative function $ f: \mathbf N \rightarrow \mathbf R $, $ f( n) \geq 0 $ for all $ n $. Let $ f, g $ be such "growth functions" . The function $ f $ is of lesser growth than $ g $, $ f < g $, if there exist a $ c > 0 $ and an $ m \in \mathbf N = \{ 1, 2 ,\dots \} $ such that $ f( n) \leq cg( nm) $ for all $ n \in \mathbf N $. Two growth functions $ f, g $ are of the same order of growth if $ f < g $ and $ g < f $. The equivalence class of $ f $ for this relation is denoted by $ [ f ] $ and is called the growth of $ f $. As in analytic function theory, one considers

$$ \rho ( f ) = { {\lim\limits \sup } } _ {n \rightarrow \infty } \ \frac{ \mathop{\rm log} \mathop{\rm log} f( n) }{ \mathop{\rm log} n } , $$

the order of growth of $ f $, which only depends on $ [ f ] $. The function $ n \mapsto 2 ^ {n} $ has order of growth 1, or exponential growth. This is the highest that is of interest (and can occur) in the present context. A function $ f $ is of polynomial growth, or power growth, $ r $ if $ f \in [ n ^ {r} ] $. Given that $ \rho ( f ) = 0 $, the polynomial growth power $ r $ is found from

$$ r( f ) = {\lim\limits \sup } _ {n \rightarrow \infty } \ \frac{ \mathop{\rm log} f( n) }{ \mathop{\rm log} n } . $$

If the growth of $ f $ satisfies the inequalities $ [ 2 ^ {n} ] > [ f ] > [ n ^ {r} ] $ for all $ r > 0 $, the function $ f $ is said to be of intermediate growth.

The growth function for a finitely-generated group was defined above. The growth of $ [ f _ {G} ] $ does not depend on the chosen system of generators and is hence an invariant of $ G $. The growth of a finitely-generated free group on $ \geq 2 $ generators is exponential. A finitely-generated nilpotent group has polynomial growth.

For an algebra $ A $ over a field $ k $( associative, Lie, etc.) the definition is as follows.

Let $ a _ {1} \dots a _ {r} $ be a set of generators of $ A $ over $ k $, so that every $ a \in A $ is a $ k $- linear combination of monomials in the $ a _ {i} $. Let $ V $ be the vector space spanned by the $ a _ {i} $. Let $ V ^ {k} $ be the vector subspace of $ A $ of all $ k $- linear combinations of products $ v _ {1} \dots v _ {k} $, $ v _ {i} \in V $. Then the function

$$ f _ {A} ( n) = \sum_{i=1}^ { n } \mathop{\rm dim} V ^ {i} $$

is the growth function of $ A $( with respect to the generating subspace $ V $). The growth of $ f _ {A} $ does not depend on the choice of $ V $. The growth of the group algebra $ k[ G] $ is the growth of $ G $.

If $ W = \oplus_{n=0}^ \infty W ^ {n} $ is a graded vector space, one defines the series

$$ h _ {W} ( z) = \sum_{n=0}^ \infty \mathop{\rm dim} ( W ^ {n} ) z ^ {n} . $$

This series is called the Hilbert series, Poincaré series, Hilbert–Poincaré series, or Poincaré–Betti series, depending on the context. There is an associated growth function

$$ g _ {W} ( n) = \sum_{i=0}^ { n } \mathop{\rm dim} ( W ^ {i} ). $$

If $ A = \oplus_{n=0}^ \infty A ^ {(n)} $ is a finitely-generated graded algebra, then the growth function coming from the grading and any growth function defined by a finite-dimensional generating vector space have the same growth.

For graphs one also defines a growth function. Let $ G = ( V, E) $ be a finite oriented graph, possibly with loops and multiple edges. Let $ c _ {G} ( m) $ be the number of paths of length $ m $. Then the Poincaré series of the graph $ G $ is

$$ P _ {G} ( z) = \sum_{m=0}^ \infty c _ {G} ( m) z ^ {m} , $$

and the growth function of $ G $ is $ f _ {G} ( m) = \sum_{i=0}^ {m} c _ {G} ( m) $. Here a path of length $ m $ is a sequence of vertices and edges $ v _ {1} e _ {1} v _ {2} \dots e _ {m-1} v _ {m} $ such that $ e _ {i} $ goes from $ v _ {i} $ to $v_{i+1}$.

There are two central questions concerning Poincaré series and growth functions.

i) In the graded case: Is the Poincaré series rational?

ii) In all cases: Is it true for a suitable class of algebras or groups that all objects either have polynomial or exponential growth?

A positive answer to i) (in the graded case) implies a positive answer to ii).

The Poincaré series of a graph is a rational function of the form $ P _ {G} ( z) = q( z) p( z) ^ {-1} $ with $ p( z) = 1- a _ {1} z - \dots - a _ {n} z ^ {n} $, the reciprocal polynomial to the minimal polynomial $ m( z) = z ^ {n} - a _ {1} z ^ {n-1} - \dots - a _ {n} $ of the incidence matrix $ B $ of $ G $, where $ b _ {ij} $ is the number of edges from vertex $ i $ to vertex $ j $. In particular, the growth of a graph is either polynomial or exponential, [a13].

There are many algebras for which the associated growth functions and Poincaré series have been considered. For instance, for a local ring, $ ( A, m) $, the Poincaré series of $ \oplus m ^ {i} / m ^ {i+1} $, cf. Local ring. For an associative nilpotent ring over $ k $ one considers the graded algebra $ \mathop{\rm Ext} _ {\widetilde{N} } {} ^ {*} ( k , k) $, the Yoneda $ \mathop{\rm Ext} $- algebra, where $ \widetilde{N} = N \oplus k $ is the algebra over $ k $ obtained by adjoining a unit. For a local ring $ R $ one also considers $ \mathop{\rm Ext} _ {R} ^ {*} ( k, k) $, where now $ k $ is the residue field of $ R $. In topology one consider the graded algebra of the homology (or cohomology) of the loop space $ \Omega X $ of a space $ X $. In all these cases there are relations (established or conjectured) between the properties of the Poincaré series (such as rationality, rate of convergence, etc.) and properties of the algebras or topological spaces involved.

There are a variety of constructions associating graphs to algebras, spaces to algebras, algebras to spaces, algebras to graphs, and corresponding relations between the associated growth functions and Poincaré series, cf. [a1], [a13]–[a15].

The growth problem for commutative local rings is settled by the following result. Let $ ( R, \mathfrak m ) $ be a local ring and consider its Betti numbers $ b _ {i} ( R) = \mathop{\rm dim} _ {k} ( \mathop{\rm Ext} _ {R} ^ {i} ( k, k)) = \mathop{\rm dim} _ {k} \mathop{\rm Tor} _ {i} ^ {R} ( k, k) $, i.e. the coefficients of its Poincaré series. Then there are two possibilities, [a16]: either $ b _ {i} $ is a polynomial in $ i $, which happens if and only if $ R $ is a complete intersection, or there exist integers $ N $ and $ d > c > 1 $ such that $ c ^ {i} < b _ {i} < d ^ {i} $ for all $ i \geq N $. This implies immediately a positive solution to the Golod–Gulliksen conjecture, which stated that a local ring is a complete intersection if and only if the radius of convergence of its Poincaré series is $ \geq 1 $. Indeed one has, [a16], [a17], that the radius of convergence is $ \infty $ if and only if $ R $ is regular (cf. Local ring), that it is precisely 1 if and only if $ R $ is an irregular complete intersection and that it is strictly between 0 and 1 otherwise.

The concept of a complete intersection local ring corresponds to a complete intersection in algebraic geometry, i.e. varieties in $ \mathbf P ^ {N} $ of codimension $ i $ determined by $ i $ equations. In algebraic terms this can be described as follows.

Let $ ( R, \mathfrak m ) $ be a commutative Noetherian local ring, $ n = \mathop{\rm dim} _ {k} \mathfrak m / \mathfrak m ^ {2} $( sometimes called the embedding dimension of $ R $). Choose a basis for $ \mathfrak m / \mathfrak m ^ {2} $ and consider the corresponding Koszul complex $ E _ {*} $. Let $ \epsilon _ {j} = \mathop{\rm dim} _ {k} H _ {j} ( E _ {*} ) $. The local ring $ ( R, \mathfrak m ) $ is a complete intersection if $ e _ {1} = n- \mathop{\rm dim} R $. A Noetherian local ring is a complete intersection if and only if its completion $ ( \widehat{R} , \widehat{ {\mathfrak m }} ) $ is a complete intersection, and this is the case if and only if $ \widehat{R} $ is a quotient of a complete regular local ring $ \widetilde{R} $ by an ideal generated by a regular $ \widetilde{R} $- sequence (cf. Koszul complex). For commutative Noetherian local rings one has the chain of implications: regular $ \Rightarrow $ complete intersection $ \Rightarrow $ Gorenstein $ \Rightarrow $ Cohen–Macaulay. Cf. also Gorenstein ring and Cohen–Macaulay ring.

Cf. [a1] for a recent survey concerning these and other results on growth and rationality for algebras and spaces.

For groups there are, among others, the following theorems.

The Milnor–Wolf theorem: A finitely-generated solvable group is either of polynomial growth or of exponential growth. In the first case it is polycyclic and almost nilpotent (i.e. has a nilpotent subgroup of finite index), [a8], [a9].

The Gromov–Milnor theorem: A finitely-generated group is of polynomial growth if and only if it is almost nilpotent, [a9], [a6].

There are groups of intermediate growth [a2].

Tits' theorem: A finitely-generated subgroup of a connected Lie group has either exponential growth or is almost nilpotent (and hence has polynomial growth), [a7].

There are relations between the geometry of manifolds and the growth of its fundamental group. Probably the oldest one is due to A.S. Shvarts, [a5]. Let $ M $ be a connected compact manifold with fundamental group $ G = \pi _ {1} ( M) $. Let $ \widetilde{M} $ be the universal covering space of $ M $. Give $ M $ a Riemannian metric $ g $ and consider the induced metric $ \widetilde{g} $ on $ \widetilde{M} $. ( $ M $ and $ \widetilde{M} $ are locally the same.) Take an arbitrary point $ \widetilde{p} \in \widetilde{M} $ and let $ v( s) $ be the volume of the ball of radius $ s $ in $ \widetilde{M} $ with centre $ \widetilde{p} $. The growth of $ v $ does not depend on $ g $ or $ \widetilde{p} $ and is hence an invariant of $ M $. It is called the volume invariant, [a4]. The Shvarts theorem now says that the volume invariant of $ M $ is the growth of $ \pi _ {1} ( M) $.

A mapping $ \phi $ from a metric space $ ( M, d) $ to another $ ( M ^ \prime , d ^ \prime ) $ is called globally expanding if $ d ^ \prime ( \phi ( x), \phi ( y)) > d( x, y) $ for all $ x \neq y $. It is called locally expanding, or just expanding, if each point has an open neighbourhood on which $ \phi $ is globally expanding. The mapping $ z \mapsto z ^ {2} $ from the circle into itself is locally expanding (but not globally). Franks' polynomial growth theorem says that if a compact manifold admits an expanding self-mapping, then its fundamental group is of polynomial growth, cf. [a6].

The Milnor fundamental group growth theorems are the following, [a3]. If $ M $ is a complete $ n $- dimensional Riemannian manifold with an everywhere positive semi-definite mean curvature tensor $ R _ {ij} $, then the growth of every finitely-generated subgroup of $ \pi _ {1} ( M) $ is polynomial. On the other hand, if $ M $ is a compact Riemannian manifold with all sectional curvatures less than zero, then the fundamental group is of exponential growth.

One application of growth theory was to the class field tower problem, cf. Class field theory and Tower of fields. Let $ G $ be a group and $ \mathbf F _ {p} $ the field of $ p $ elements, $ p $ a prime number. Let $ A = \mathbf F _ {p} [ G] $ be the group algebra of $ G $ over $ \mathbf F _ {p} $ and let $ \mathfrak a $ be the augmentation ideal of $ A $, i.e. the ideal generated by the elements $ g- 1 \in R $, $ g \in G $. The Zassenhaus filtration is the sequence of characteristic subgroups $ G _ {n} = \{ {g \in G } : {g- 1 \in \mathfrak a ^ {n} } \} $. The sequence $ \{ G _ {n} \} $ is also called the lower $ p $- central series of $ G $. Let $ \widehat{A} $ be the associated graded ring defined by $ \mathfrak a $, i.e.

$$ \widehat{A} = \oplus_{n=0}^ \infty {\widehat{A} } _ {n} ,\ \ {\widehat{A} } _ {n} = \mathfrak a ^ {n} / \mathfrak a ^ {n+1} . $$

Let $ f _ {G} ( z) $ be the associated Hilbert series

$$ f _ {G} ( z) = \sum_{n=0}^ \infty \mathop{\rm dim} ( {\widehat{A} } _ {n} ) z ^ {n} , $$

where $ \mathop{\rm dim} = \mathop{\rm dim} _ {\mathbf F _ {p} } $ and it is assumed that $ \mathop{\rm dim} {\widehat{A} } _ {n} < \infty $, which is guaranteed if $ \mathop{\rm dim} {\widehat{A} } _ {1} < \infty $. Let $ G = F/R $, where $ F $ is a free group on $ d \geq 2 $ generators, and let $ S $ be a set of defining words for $ G $. For each $ s \in S $, let $ d ( s) = \sup \{ {n } : {s \in F _ {n} } \} $, where $ F _ {n} $ is the Zassenhaus filtration of $ F $. Let $ l _ {n} = \# \{ {s \in S } : {d( s) = n } \} $, $ l _ {0} = 1 $. Then the Golod–Shafarevich theorem says: 1) $ \mathop{\rm dim} {\widehat{A} } _ {n} \geq d( \mathop{\rm dim} ( {\widehat{A} } _ {n-1} )) - \sum _ {k=0}^ {n-1} l _ {n-k} $; and 2) if $ l _ {n} \leq ( d- 1) ^ {2} /4 $ for all $ n $, then the algebra $ A $ is infinite dimensional, [a11], [a12]. This theorem was a main ingredient in the negative solution of the class field tower problem; that is, in the construction of infinite class field towers.

Still another application is Lazard's theorem [a10], which provides a criterion for the analyticity of a pro- $ p $- group in terms of the Hilbert series of the associated algebra.

References

[a1]	I.K. Babenko, "Problems of growth and rationality in algebra and topology" Russian Math. Surv. , 41 : 2 (1986) pp. 117–175 Uspekhi Mat. Nauk , 41 : 2 (1986) pp. 95–142 MR0842162 Zbl 0607.55007
[a2]	R.I. Grigorchuk, "On Milnor's problem of group growth" Soviet Math. Dokl. , 28 (1983) pp. 23–26 Dokl. Akad. Nauk SSSR , 271 (1983) pp. 30–33 MR712546
[a3]	J. Milnor, "A note on curvature and fundamental group" J. Diff. Geom. , 2 (1968) pp. 1–7 MR0232311 Zbl 0162.25401
[a4]	V. Efremovich, "On proximity geometry of Riemannian manifolds" Transl. Amer. Math. Soc. (2) , 39 (1964) pp. 167–170 Uspekhi Mat. Nauk , 8 (1953) pp. 189–191 Zbl 0152.39201
[a5]	A. Shvarts, "A volume invariant of coverings" Dokl. Akad. Nauk SSSR , 105 (1955) pp. 32–34 (In Russian) Zbl 0066.15903
[a6]	M. Gromov, "Groups of polynomial growth and expanding maps" Publ. Math. IHES , 53 (1981) pp. 53–73 MR0623535 MR0623534 Zbl 0474.20018
[a7]	J. Tits, "Free subgroups in linear groups" J. of Algebra , 20 (1972) pp. 250–270 MR0286898 Zbl 0257.20031 Zbl 0236.20032
[a8]	J.A. Wolf, "Growth of finitely generated solvable groups and curvature of Riemannian manifolds" J. Diff. Geom. , 2 (1968) pp. 421–446 Zbl 0207.51803
[a9]	J.W. Milnor, "Growth of finitely generated solvable groups" J. Diff. Geom. , 2 (1968) pp. 447–449 MR0244899 Zbl 0176.29803
[a10]	M. Lazard, "Groupes analytiques 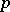-adiques" Publ. Math. IHES , 26 (1965) pp. 389–603 MR209286
[a11]	E.S. Golod, I.R. Shafarevich, "On class field towers" Transl. Amer. Math. Soc. (2) , 48 (1965) pp. 91–102 Izv. Akad. Nauk SSSR Ser. Mat. , 28 (1964) pp. 261–272 Zbl 0148.28101
[a12]	H. Koch, "Galoissche Theorie der 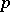-Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970)
[a13]	V.A. Ufnarovskii, "A criterion for the growth of graphs and algebras defined by words" Math. Notes , 31 (1982) pp. 238–241 Mat. Zametki , 31 (1982) pp. 465–472
[a14]	J.-E. Roos, "Relations between the Poincaré–Betti series of loop spaces and of local rings" M.P. Malliavin (ed.) , Sem. Alg. P. Dubreil , Lect. notes in math. , 740 , Springer (1979) pp. 285–322 MR563510 Zbl 0415.13012
[a15]	C. Löfwall, "On the subalgebra generated by one dimensional elements in the Yoneda Ext-algebra" , Preprint Dept. Math. , Univ. Stockholm (1976) Zbl 0429.13008
[a16]	L. Avramov, "Local algebra and rational homotopy" Astérisque , 113–114 (1984) pp. 15–43 MR0749041 Zbl 0552.13003
[a17]	L. Avramov, "Local rings of finite simplicial dimension" Bull. Amer. Math. Soc. , 10 (1984) pp. 289–291 MR0733698 Zbl 0552.13005