Plessner theorem
One of the basic results in the theory of boundary properties of analytic functions. Let $ f( z) $
be a meromorphic function in the unit disc $ D = \{ {z \in \mathbf C } : {| z | < 1 } \} $
and let $ \Delta = \Delta ( e ^ {i \theta } ) $
be the open angle with vertex $ e ^ {i \theta } $
on the circle $ \Gamma = \{ {z \in \mathbf C } : {| z | = 1 } \} $
formed by two chords of $ D $
passing through $ e ^ {i \theta } $.
The point $ e ^ {i \theta } $
is called a Plessner point (or it is said that $ e ^ {i \theta } $
has the Plessner property) if in every arbitrarily small angle $ \Delta $
there exists a sequence $ \{ z _ {k} \} \subset \Delta $
such that
$$ \lim\limits _ {k \rightarrow \infty } z _ {k} = e ^ {i \theta } ,\ \ \lim\limits _ {k \rightarrow \infty } f( z _ {k} ) = w $$
for every value $ w $ in the extended complex plane $ \overline{\mathbf C}\; $. The point $ e ^ {i \theta } $ is called a Fatou point for $ f( z) $ if there exists a single unique limit
$$ \lim\limits f( z) = A $$
as $ z $ tends to $ e ^ {i \theta } $ within any angle $ \Delta $. Plessner's theorem [1]: Almost-all points on $ \Gamma $ with respect to the Lebesgue measure on $ \Gamma $ are either Fatou points or Plessner points.
It is also known that the set $ P( f ) $ of all Plessner points has type $ G _ \delta $ on $ \Gamma $. Examples have been constructed of analytic functions in $ D $ for which $ P( f ) $ is dense on $ \Gamma $ and has arbitrary given Lebesgue measure $ \mathop{\rm mes} P( f ) = m $, $ 0 \leq m < 2 \pi $[3]. Plessner's theorem applies to any meromorphic function $ f( z) $ in any simply-connected domain $ D $ with a rectifiable boundary $ \Gamma $. In that case, $ \zeta \in \Gamma $ is a Fatou point if the following limit exists (cf. also Cluster set):
$$ \lim\limits f( z) = A,\ \ z \in D, $$
as $ z \rightarrow \zeta $ along any non-tangential path; the definition of a Plessner point $ \zeta \in \Gamma $ must be altered in such a way that one considers angles $ \Delta $ with vertex $ \zeta $ and sides forming angles less than $ \pi /2 $ with the normal to $ \Gamma $ at $ \zeta $[2].
Meier's theorem is an analogue of Plessner's theorem in terms of categories of sets (cf. Meier theorem).
References
| [1] | A.I. Plessner, "Über das Verhalten analytischer Funktionen auf dem Rande des Definitionsbereiches" J. Reine Angew. Math. , 158 (1928) pp. 219–227 |
| [2] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [3] | A.J. Lohwater, "The boundary behaviour of analytic functions" Itogi Nauk. i Tekhn. Mat. Anal. , 10 (1973) pp. 99–259 (In Russian) |
Comments
Angles of the form $ \Delta $ are called Stolz angles.
A good reference is [a3], to which [3] is a Russian sequel.
Plessner's theorem has a complete analogue for the unit ball in $ \mathbf C ^ {n} $, cf. [a1]: Every holomorphic function on the unit ball decomposes the boundary into three measurable sets, as in the classical case.
References
| [a1] | W. Rudin, "Function theory in the unit ball in 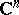 " , Springer (1981) " , Springer (1981) |
| [a2] | M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1975) |
| [a3] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 9 |
| [a4] | K. Noshiro, "Cluster sets" , Springer (1960) |
Plessner theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Plessner_theorem&oldid=48190