Pi-separable group

A group which has a normal series such that the order of every factor contains at most one prime from $\pi$ ($\pi$ is a set of prime numbers). The class of $\pi$-separable groups contains the class of $\pi$-solvable groups (cf. $\pi$-solvable group). For finite $\pi$-separable groups, the $\pi$-Sylow properties (cf. Sylow theorems) have been shown to hold (see [1]). In fact, for any set $\pi_1\subseteq\pi$, a finite $\pi$-separable group $G$ contains a $\pi_1$-Hall subgroup (cf. also Hall subgroup), and any two $\pi_1$-Hall subgroups are conjugate in $G$. Any $\pi_1$-subgroup of a $\pi$-separable group $G$ is contained in some $\pi_1$-Hall subgroup of $G$ (see [2]).

References

[1]	S.A. Chunikhin, "On 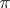-separable groups" Dokl. Akad. Nauk SSSR , 59 : 3 (1948) pp. 443–445 (In Russian)
[2]	P. Hall, "Theorems like Sylow's" Proc. London Math. Soc. , 6 : 22 (1956) pp. 286–304

Comments

Chunikhin's theorem says that if $k$ is a divisor of the order $n$ of a $\pi$-separable group such that $n=kl$, $(k,l)=1$, and if all prime divisors of $k$ are in $\pi$, then $G$ has a subgroup of order $k$ and all these subgroups are conjugate in $G$. If $\pi$ consists of all prime numbers this becomes Hall's first theorem.

Gol'berg's theorem, [a2], says that if $G$ is a finite $\pi$-separable group and $\pi_1$ is a subset of $\pi$, then $G$ has a Sylow $\pi_1$-basis (cf. Sylow basis) and all these bases are conjugate.

References

[a1]	A.G. Kurosh, "The theory of groups" , 2 , Chelsea (1956) pp. 195ff (Translated from Russian)
[a2]	P.A. Gol'berg, "Sylow bases of $\pi$-separable groups" Dokl. Akad. Nauk SSSR , 60 (1949) pp. 615–618 (In Russian)
[a3]	S.A. Chunikhin, "On $\pi$-properties of finite groups" Mat. Sb. , 25 (1949) pp. 321–346 (In Russian)