Persian curve

spiric curve

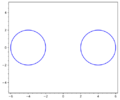
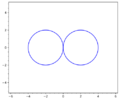
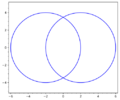
A plane algebraic curve of order four that is the line of intersection between the surface of a torus and a plane parallel to its axis (see Figures). The equation in rectangular coordinates is

$$(x^2+y^2+p^2+d^2-r^2)^2=4d^2(x^2+p^2),$$

where $r$ is the radius of the circle describing the torus, $d$ is the distance from the origin to its centre and $p$ is the distance from the axis of the torus to the plane. The following are Persian curves: the Booth lemniscate, the Cassini oval and the Bernoulli lemniscate.

• 

  $d>r$

• 

  $d=r$

• 

  $d<r$

The name is after the Ancient Greek geometer Persei (2nd century B.C.), who examined it in relation to research on various ways of specifying curves.

References

[1]	A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)
[a1]	F. Gomez Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971)
[a2]	K. Fladt, "Analytische Geometrie spezieller ebener Kurven" , Akad. Verlagsgesell. (1962)