Parabolic cylinder function
Weber function, Weber–Hermite function
A solution of the differential equation
$$ \tag{* } \frac{d ^ {2} y }{dz ^ {2} } + \left ( \nu + \frac{1}{2} - \frac{z ^ {2} }{4} \right ) y = 0, $$
which is obtained as a result of separating the variables in the wave equation $ \Delta u = k ^ {2} u $ in parabolic cylindrical coordinates (cf. Parabolic coordinates). Ordinarily one uses the solution
$$ D _ \nu ( z) \equiv U \left ( - \nu - \frac{1}{2} , z \right ) = \ 2 ^ {( \nu - 1)/2 } e ^ {- z ^ {2} /4 } \Psi \left ( \frac{1 - \nu }{2} , \frac{3}{2} ; \ \frac{z ^ {2} }{2} \right ) , $$
where $ \Psi ( a, b; z) $ is the confluent hypergeometric function. The functions $ D _ \nu (- z) $ and $ D _ {- \nu - 1 } (\pm iz) $ also satisfy equation (*). The functions $ D _ \nu ( z) $ and $ D _ {- \nu - 1 } (\pm iz) $ are linearly independent for arbitrary $ \nu $, and $ D _ \nu ( z) $ and $ D _ \nu (- z) $ are linearly independent for $ \nu \neq 0, \pm 1 , \dots $. The parabolic cylinder functions are entire functions of $ z $. The function $ D _ \nu ( z) $ is real for real $ \nu $ and $ z $.
The differentiation formulas are, $ n = 1, 2 ,\dots $:
$$ \frac{d ^ {n} }{dz ^ {n} } \left [ e ^ {z ^ {2} /4 } D _ \nu ( z) \right ] = \ (- 1) ^ {n} (- \nu ) _ {n} e ^ {z ^ {2} /4 } D _ {\nu - n } ( z), $$
$$ \frac{d ^ {n} }{dz ^ {n} } \left [ e ^ {- z ^ {2} /4 } D _ \nu ( z) \right ] = (- 1) ^ {n} e ^ {- z ^ {2} /4 } D _ {\nu + n } ( z) . $$
The recurrence formulas are:
$$ D _ {\nu + 1 } ( z) - zD _ \nu ( z) + \nu D _ {\nu - 1 } ( z) = 0, $$
$$ D _ \nu ^ \prime ( z) + \frac{z}{2} D _ \nu ( z) - \nu D _ {\nu - 1 } ( z) = 0, $$
$$ D _ \nu ^ \prime ( z) - \frac{z}{2} D _ \nu ( z) + D _ {\nu + 1 } ( z) = 0. $$
Asymptotically, for fixed $ \nu $ and $ | \mathop{\rm arg} z | < 3 \pi /4 $, as $ z \rightarrow \infty $, one has
$$ D _ \nu ( z) = \ z ^ \nu e ^ {- z ^ {2} /4 } \left [ \sum _ { k= 0} ^ { N } \frac{(- \nu /2) _ {k} ( 1/2 - \nu /2) _ {k} }{k!} \left ( \frac{z ^ {2} }{- 2} \right ) ^ {- k}\right .+ \left . O ( | z | ^ {- 2N- 2 } ) \right ] , $$
and, for bounded $ | z | $ and $ | \mathop{\rm arg} ( - \nu ) | \leq \pi /2 $, as $ | \nu | \rightarrow \infty $, one has
$$ D _ \nu ( z) = \ \frac{1}{\sqrt 2 } \mathop{\rm exp} \left [ \frac \nu {2} \mathop{\rm ln} (- \nu ) - \frac \nu {2} - \sqrt {- \nu } z \right ] \left [ 1 + O \left ( \frac{1}{\sqrt {| \nu | } } \right ) \right ] . $$
Parabolic cylinder functions are related to other functions as follows ($ n = 0, 1 , \dots $): To the Hermite polynomials by
$$ D _ {n} ( z) = \ 2 ^ {- n/2} e ^ {- z ^ {2} /4 } H _ {n} \left ( \frac{z}{\sqrt 2} \right ) , $$
to the probability integral (error function) by
$$ D _ {-} n- 1 ( z) = \ \frac{(- 1) ^ {n} \sqrt 2 }{n!} e ^ {- z ^ {2} /4 } \frac{d ^ {n} }{dz ^ {n} } \left ( e ^ {z ^ {2} /3 } \mathop{\rm erfc} \frac{z}{\sqrt z } \right ) , $$
and to the Bessel functions by
$$ D _ {- 1/2} ( z) = \ \sqrt { \frac{\pi z }{2} } K _ {1/4} \left ( \frac{z ^ {2} }{4} \right ) . $$
References
| [1] | H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953) |
| [2] | J.C.P. Miller, "Giving solutions of the differential equation 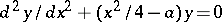 , tables of Weber parabolic cylinder functions" , H.M. Stationary Office (1955) , tables of Weber parabolic cylinder functions" , H.M. Stationary Office (1955) |
Parabolic cylinder function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parabolic_cylinder_function&oldid=52277