Oscillations, theory of
The branch of the applied theory of differential equations connected with the study of oscillatory phenomena in natural science and technology. The fundamental problems of the theory of oscillations consist in proving the existence of, and the actual determination of, oscillatory (periodic, almost-periodic, etc.) motions that are solutions of a given system, and the study of the behaviour of the other solutions in relation to the given oscillations. One makes a distinction between the theory of linear oscillations and the theory of non-linear oscillations.
In the theory of linear oscillations the matter reduces to the study of linear systems of differential equations, and this is usually connected with the fact that the quantities under consideration (the unknown functions of the system of differential equations) are so small that it proves possible to ignore the non-linear terms on the right-hand sides of the system. One considers linear systems of differential equations:
$$ \tag{1 } \frac{dx}{dt} = P ( t) x + f ( t) , $$
where $ x ( t) $ and $ f ( t) $ are $ n $- dimensional vectors, $ P ( t) $ is a square matrix of order $ n $, and most often $ P ( t) $ and $ f ( t) $ are periodic or almost-periodic functions (cf. Linear system of differential equations with almost-periodic coefficients; Linear system of differential equations with periodic coefficients). The main problem in the theory of linear oscillations: To construct periodic and almost-periodic solutions of the system (1), and to investigate their stability properties. From this point of view the situation that is studied in greatest detail is when the given system is close to a system that has already been studied, in other words, those cases when it has been possible to introduce a small parameter as follows:
$$ \tag{2 } \frac{dx}{dt} = \ ( P ( t) + \mu Q ( t , \mu ) ) x + f ( t), $$
under the hypothesis that the system
$$ \tag{3 } \frac{dx}{dt} = P ( t) x $$
has been fully investigated and $ \mu $ is a small parameter. For such systems it is possible in the majority of cases to investigate the question of the existence of periodic (respectively, almost-periodic) solutions and to actually construct them. Under very broad assumptions concerning the matrices $ P $ and $ Q $, a representation of the characteristic exponents of the system (3) has been given in the form of functions of the parameter (see [7], [10]); in particular, the interesting phenomenon of parametric resonance in linear systems has been studied [5] (cf. Parametric resonance, mathematical theory of).
In the theory of non-linear oscillations, both in the statement of the problems and in the methods of investigating them, the so-called local and non-local problems are essentially different. Relating to the former are those problems in which it is possible to isolate a certain "smallness" (for example, the quantities under investigation are themselves small, or there are small parameters in the system).
If the required functions in the problem under investigation can be considered small, then the matter reduces to the investigation of a neighbourhood of the equilibrium state for the system of differential equations
$$ \tag{4 } \frac{dx}{dt} = X ( x , t ) , $$
where $ x ( t) $ and $ X ( x , t ) $ are $ n $- dimensional vectors and $ X ( 0 , t) \equiv 0 $. Here methods of the local qualitative theory of differential equations of the form (4) (cf. Qualitative theory of differential equations) and methods of the theory of Lyapunov stability of motion [1] have broad application. A very important result in the theory of non-linear oscillations was obtained by A.N. Kolmogorov and his followers (see [4]). He proved the existence of quasi-periodic solutions in a neighbourhood of the equilibrium state $ x = 0 $ for the system (4).
Small parameters often enter into the data of the system of differential equations, that is, systems of the form
$$ \tag{5 } \frac{dx}{dt} = \ X ( x , t ) + \mu R ( x , t , \mu ) $$
are considered, where $ \mu $ is a small parameter. Related to this type of systems is the following problem. Along with the system (5) the so-called "generating" system is considered; this is the system to which (5) reduces when $ \mu = 0 $, in other words, a system of type (4). It is assumed that the "generating" system possesses a certain property. The following question is posed: Does (5) possess the same property for small non-zero values of $ \mu $? For example, suppose that (4) has a periodic or almost-periodic solution $ x = \psi ( t) $. Then does (5) have a periodic or almost-periodic solution $ x = \phi ( t , \mu ) $ such that
$$ \lim\limits _ {\mu \rightarrow 0 } \phi ( t , \mu ) = \psi ( t) ? $$
H. Poincaré [2] developed powerful methods for the solution of this type of problem. In many cases he not only proved the existence of a periodic solution, but also indicated an algorithm for constructing it (see, for example, [5]).
N.M. Krylov, N.N. Bogolyubov and their students (see [3], [6], [11]) have developed asymptotic methods for systems of the type (5). Of special importance among these methods is the Krylov–Bogolyubov method of averaging, which is as follows. The following so-called standard system is considered:
$$ \tag{6 } \frac{dx}{dt} = \ \mu X ( x , t , \mu ) . $$
It turns out that many systems in the theory of non-linear oscillations lead to the above system. Along with (6) the "averaged" system
$$ \tag{7 } \frac{dy}{dt} = \mu Y ( y) $$
is considered, where
$$ Y = \ \lim\limits _ {t \rightarrow \infty } \frac{1}{t} \int\limits _ { 0 } ^ { t } X ( x , \tau , 0 ) d \tau . $$
Krylov and Bogolyubov have shown that (7) approximates (6) up to quantities of order $ \mu ^ {2} $. By means of further averaging it is possible to get rid of the dependence on $ t $ in the terms of any desired order of smallness in $ \mu $. However, this process usually diverges, so that this method is essentially asymptotic.
The method of integral surfaces (cf. Integral surface) plays a very important role in the theory of non-linear oscillations. The foundations of this method were laid by A.M. Lyapunov [1]. Under very broad hypotheses it can be proved (see [3], [6], [11]) that if the "generating" system (4) has an integral surface with specified properties, then (5) also has such an integral surface.
The theory of relaxation oscillations (cf. Relaxation oscillation) is closely related to the above circle of problems. These oscillations are described by systems of differential equations with small parameters in front of the derivative:
$$ \tag{8 } \frac{dx}{dt} = \ X ( x , y , t , \mu ) ,\ \ \mu \frac{dy}{dt} = \ Y ( x , y , t , \mu ) , $$
where $ x $ and $ X $ are $ n $- dimensional vectors, $ y $ and $ Y $ are $ m $- dimensional vectors and $ \mu $ is a small parameter. Along with the system (8) the following degenerate system is considered:
$$ \tag{9 } \frac{dx}{dt} = \ X ( x , y , t , 0 ) ,\ \ Y ( x , y , t , 0 ) = 0 . $$
If (9) has a special "discontinuous" periodic solution, then in a number of cases (8) has a true periodic solution for small $ \mu $( see [12]).
In applications one very often encounters systems of differential equations in which it is not possible to single out any smallnesses. Here one runs into non-local problems of the theory of oscillations. In the study of non-local problems very serious difficulties arise. However, in a number of particular cases, which are nevertheless important in applications, one can successfully carry out the complete investigation of the corresponding system or obtain fairly significant information about the behaviour of its solutions. For example, for the equation
$$ \tag{10 } \dot{x} dot + f ( x) \dot{x} + g ( x) = 0 , $$
which is a generalization of the van der Pol equation, N. Levinson and O.K. Smit [15] have proved the existence, stability and uniqueness of the limit cycle. In the proof essential use is made of the fact that (10) is a second-order equation. Subsequently the existence was proved of a periodic solution for a non-linear equation of order three and for various autonomous systems of higher orders.
In the study of periodic non-autonomous systems, that is, systems of the form (4) for which $ X ( x , t + \omega ) = X ( x , t ) $, one associates with the system its Poincaré transformation $ T $. It is introduced by the formula $ T x _ {0} = x ( \omega , 0 , x _ {0} ) $, where $ x ( t , t _ {0} , x _ {0} ) $ is the solution of (4) such that $ x ( t _ {0} , t _ {0} , x _ {0} ) = x _ {0} $. If $ x ^ {*} $ is a fixed point of the transformation $ T $, then the solution $ x ( t , 0 , x ^ {*} ) $ has period $ \omega $ in $ t $. This provides the possibility of applying various fixed-point theorems (see [8], [9]) for the proof of the existence of periodic solutions.
In the theory of non-linear oscillations, dissipative systems play an important role (these are systems of type (4) the solutions to which remain in a fixed ball for sufficiently large $ t $, cf. Dissipative system) and systems with convergences (in such systems all solutions converge to a single stable solution); fairly reliable methods have been developed for the proof of convergence and dissipativeness of concrete systems [8].
The behaviour of the solutions of a dissipative periodic system is on the whole determined by the structure of some asymptotically-stable integral set of this system. Therefore the study of the structure of such sets is essential for the theory of non-linear oscillations. In the case when the given system has only a finite number of periodic solutions, this set can be fairly completely characterized [13]. If, on the other hand, the system has an infinite number of periodic solutions, then the asymptotically-stable integral sets prove to have an extremely complicated structure [13]. The study of such systems is associated as a rule with overcoming considerable difficulties, and this has been successfully carried out only in exceptional cases. An example of this type of study was given by M. Cartwright and J.E. Littlewood [16] in the study of the van der Pol equation with forced vibration:
$$ \dot{x} dot + k ( x ^ {2} - 1 ) \dot{x} + x = k b \sin t . $$
In particular, they proved that this equation has infinitely many periodic solutions, for an appropriate choice of the parameters $ b $ and $ k $.
References
| [1] | A.M. Lyapunov, "Stability of motion" , Acad. Press (1966) (Translated from Russian) |
| [2] | H. Poincaré, "Les méthodes nouvelles de la mécanique céleste" , 1 , Gauthier-Villars (1892) |
| [3] | N.M. Krylov, N.N. Bogolyubov, "Introduction to non-linear mechanics" , Princeton Univ. Press (1947) (Translated from Russian) |
| [4] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
| [5] | I.G. Malkin, "Some problems in the theory of non-linear oscillations" , Moscow-Leningrad (1956) (In Russian) |
| [6] | N.N. Bogolyubov, Yu.A. Mitropol'skii, "Asymptotic methods in the theory of non-linear oscillations" , Hindushtan Publ. Comp. , Delhi (1961) (Translated from Russian) |
| [7] | N.P. Erugin, "Linear systems of ordinary differential equations with periodic and quasi-periodic coefficients" , Acad. Press (1966) (Translated from Russian) |
| [8] | V.A. Pliss, "Non-local problems of the theory of oscillations" , Acad. Press (1961) (Translated from Russian) |
| [9] | M.A. Krasnosel'skii, "The operator of translation along trajectories of differential equations" , Amer. Math. Soc. (1968) (Translated from Russian) |
| [10] | V.A. Yakubovich, V.M. Starzhinskii, "Linear differential equations with periodic coefficients" , Wiley (1975) (Translated from Russian) |
| [11] | Yu.A. Mitropol'skii, O.B. Lykova, "Integral manifolds in non-linear mechanics" , Moscow (1973) (In Russian) |
| [12] | E.F. Mishchenko, N.Kh. Rozov, "Differential equations with small parameters and relaxation oscillations" , Plenum (1980) (Translated from Russian) |
| [13] | V.A. Pliss, "Integral sets of periodic systems of differential equations" , Moscow (1977) (In Russian) |
| [14] | V.I. Arnol'd, "Small denominators and problems of stability of motion in classical and celestial mechanics" Russian Math. Surveys , 18 : 6 (1963) pp. 86–191 Uspekhi Mat. Nauk , 18 : 6 (1963) pp. 91–192 |
| [15] | N. Levinson, O.K. Smit, "A general equation for relaxation oscillations" Duke Math. J. , 9 (1942) pp. 382–403 |
| [16] | J.E. Littlewood, "The equation 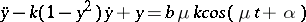 for large for large 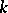 , and its generalizations" Acta Math. , 97 : 3–4 (1957) pp. 267–308 , and its generalizations" Acta Math. , 97 : 3–4 (1957) pp. 267–308 |
Comments
References
| [a1] | J. Grasman, "Asymptotic methods for relaxation oscillations and applications" , Springer (1982) |
| [a2] | J.K. Hale, "Ordinary differential equations" , Wiley (1969) |
| [a3] | C. Hayashi, "Nonlinear oscillations in physical systems" , McGraw-Hill (1964) |
| [a4] | N. Minorski, "Nonlinear oscillations" , v. Nostrand (1962) (Translated from Russian) |
| [a5] | A.H. Nayfeh, D.T. Mook, "Nonlinear oscillations" , Wiley (1979) |
| [a6] | M. Roseau, "Vibrations nonlinéaires et théorie de la stabilité" , Springer (1966) |
| [a7] | J.A. Sanders, F. Verhulst, "Averaging methods in nonlinear dynamical systems" , Springer (1985) |
| [a8] | G. Schmidt, A. Tondl, "Non-linear vibrations" , Cambridge Univ. Press (1967) |
| [a9] | M. Urabe, "Nonlinear autonomous oscillations" , Acad. Press (1967) |
| [a10] | J. Guckenheimer, P. Holmes, "Non-linear oscillations, dynamical systems, and bifurcations of vector fields" , Springer (1983) |
| [a11] | A.A. Pankov, "Bounded and almost periodic solutions of operator equations" , Kluwer (1991) (Translated from Russian) |
Oscillations, theory of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Oscillations,_theory_of&oldid=48087