Operator topology
A topology on the space $ L( E, F ) $
of continuous linear mappings from one topological vector space $ E $
into another topological vector space $ F $,
converting the space $ L( E, F ) $
into a topological vector space. Let $ F $
be a locally convex space and let $ \mathfrak S $
be a family of bounded subsets of $ E $
such that the linear hull of the union of the sets of this family is dense in $ E $.
Let $ \mathfrak B $
be a basis of neighbourhoods of zero in $ F $.
The family
$$ M( S, V) = \{ {f } : {f \in L( E, F ), f( S) \subset V } \} , $$
where $ S $ runs through $ \mathfrak S $ and $ V $ through $ \mathfrak B $, is a basis of neighbourhoods of zero for a unique topology that is invariant with respect to translation, which is an operator topology and which converts the space $ L( E, F ) $ into a locally convex space; this topology is called the $ \mathfrak S $- topology on $ L( E, F ) $.
Examples. I) Let $ E, F $ be locally convex spaces. 1) Let $ \mathfrak S $ be the family of all finite subsets in $ E $; the corresponding $ \mathfrak S $- topology (on $ L( E, F ) $) is called the topology of simple (or pointwise) convergence. 2) Let $ \mathfrak S $ be the family of all convex balanced compact subsets of $ E $; the corresponding topology is called the topology of convex balanced compact convergence. 3) Let $ \mathfrak S $ be the family of all pre-compact subsets of $ E $; the corresponding $ \mathfrak S $- topology is called the topology of pre-compact convergence. 4) Let $ \mathfrak S $ be the family of all bounded subsets; the corresponding topology is called the topology of bounded convergence.
II) If $ E, F $ are Banach spaces considered simultaneously in the weak or strong (norm) topology, then the corresponding spaces $ L( E, F ) $ coincide algebraically; the corresponding topologies of simple convergence are called the weak or strong operator topologies on $ L( E, F ) $. The strong operator topology majorizes the weak operator topology; both are compatible with the duality between $ L( E, F ) $ and the space of functionals on $ L( E, F ) $ of the form $ f( A) = \sum \phi _ {i} ( A \xi _ {i} ) $, where $ \xi _ {i} \in E $, $ \phi _ {i} \in F ^ { * } $, $ A \in L( E, F ) $.
III) Let $ E, F $ be Hilbert spaces and let $ \widetilde{E} , \widetilde{F} $ be countable direct sums of the Hilbert spaces $ E _ {n} , F _ {n} $, respectively, where $ E _ {n} = E $, $ F _ {n} = F $ for all integer $ n $; let $ \psi $ be the imbedding of the space $ L( E, F ) $ into $ L( \widetilde{E} , \widetilde{F} ) $ defined by the condition that for any operator $ A \in L( E, F ) $ the restriction of the operator $ \psi ( A) $ to the subspace $ E _ {n} $ maps $ E _ {n} $ into $ F _ {n} $ and coincides on $ E _ {n} $ with the operator $ A $. Then the complete pre-image in $ L( E, F ) $ of the weak (strong) operator topology on $ L( \widetilde{E} , \widetilde{F} ) $ is called the ultra-weak (correspondingly, ultra-strong) operator topology on $ L( E, F ) $. The ultra-weak (ultra-strong) topology majorizes the weak (strong) operator topology. A symmetric subalgebra $ \mathfrak A $ of the algebra $ L( E) $ of all bounded linear operators on a Hilbert space $ E $, containing the identity operator, coincides with the set of all operators from $ L( E) $ that commute with each operator from $ L( E) $ that commutes with all operators from $ \mathfrak A $, if and only if $ \mathfrak A $ is closed in the weak (or strong, or ultra-weak, or ultra-strong) operator topology, i.e. is a von Neumann algebra.
References
| [1] | H.H. Schaefer, "Topological vector spaces" , Springer (1971) |
| [2] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Wiley, reprint (1988) |
| [3] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
| [4] | S. Sakai, "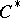 -algebras and -algebras and 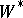 -algebras" , Springer (1971) -algebras" , Springer (1971) |
Operator topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Operator_topology&oldid=48050