Non-oscillation interval
interval of disconjugacy
A connected interval $ J $ on the real axis $ \mathbf R $ such that any non-trivial solution $ x = x ( t) $ of a given ordinary linear differential equation of order $ n $ with real coefficients,
$$ \tag{* } x ^ {(} n) + a _ {1} ( t) x ^ {(} n- 1) + \dots + a _ {n} ( t) x = 0 , $$
has on it more than $ n- 1 $ zeros, an $ m $- fold zero counted $ m $ times. Properties of solutions of (*) on a non-oscillation interval have been well studied (see, for example, [1]–[3]). There are several generalizations of the concept of a non-oscillation interval, to linear systems of differential equations, to non-linear differential equations, and also to other types of equations (difference, with deviating argument).
References
| [1] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) |
| [2] | A.Yu. Levin, "Non-oscillation of solutions of the equation 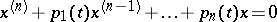 " Russian Math. Surveys , 24 : 2 (1969) pp. 43–99 Uspekhi Mat. Nauk , 24 : 2 (1969) pp. 43–96 " Russian Math. Surveys , 24 : 2 (1969) pp. 43–99 Uspekhi Mat. Nauk , 24 : 2 (1969) pp. 43–96 |
| [3] | W.A. Coppel, "Disconjugacy" , Springer (1971) |
Non-oscillation interval. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-oscillation_interval&oldid=48001