Nomography
A branch of mathematics in which methods of graphical representation of functional dependencies are studied. The resulting designs are called nomograms. Every nomogram is constructed for a definite functional dependence within specific limits of variation of the variables. In nomography computational work is replaced by the performance of the simplest geometric operations indicated in the instructions and an evaluation of the answers.
The accuracy of answers by nomography depends on the form of the nomographic presentation of the dependency, the limits of variation of the variables, the dimension of the design, and on the chosen type of nomogram. On the average, nomograms can provide answers to 2–3 true digits. When the accuracy of nomograms is insufficient, they can be used for provisional calculations, for finding zero-order approximations, and for the control of computations with the aim of discovering gross errors.
Nomograms can also be used to study functional dependencies, putting the nomograms at their foundation. Often such a study can be carried out by nomograms in a considerably simpler and more intuitive way than by other methods. By means of nomograms one can investigate the influence of various variables on the required variable, give an intuitive interpretation of some previously known properties of the dependency in question, and establish previously unknown peculiarities of it. Nomographic methods of investigation can be applied, for example, in problems on the selection of parameters in empirical formulas on the results of observations, in the approximation of one function by another, and for finding extremal values of functions.
The values of variables are represented in nomograms by marked points and marked lines. A set of marked points depending on a single variable is called a scale. The equation of scale of a variable $ \alpha _ {1} $ in a rectangular coordinate system $ x 0 y $ is written in the form
$$ x = f _ {1} ,\ \ y = g _ {1} , $$
where $ f _ {1} $ and $ g _ {1} $ are functions $ f _ {1} ( \alpha _ {1} ) $ and $ g _ {1} ( \alpha _ {1} ) $. The scheme of the scale of $ \alpha _ {1} $ is illustrated in Fig. a.
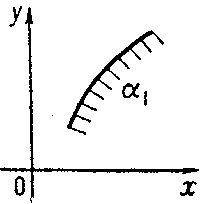
Figure: n066890a
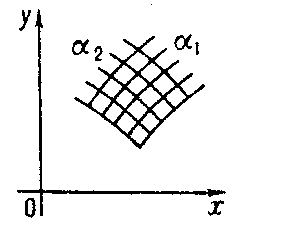
Figure: n066890b
A set of marked points depending on two variables is called a binary field. A binary field is usually formed as a grid consisting of two families of marked lines. A point in a binary field is determined as the intersection of lines with given marks. In a rectangular coordinate system $ x 0 y $ the binary field of two variables $ \alpha _ {1} $ and $ \alpha _ {2} $ is given by equations
$$ x = f _ {12} ,\ \ y = g _ {12} , $$
where $ f _ {12} $ and $ g _ {12} $ are functions $ f _ {12} ( \alpha _ {1} , \alpha _ {2} ) $ and $ g _ {12} ( \alpha _ {1} , \alpha _ {2} ) $. It is assumed that $ f _ {12} $ and $ g _ {12} $ are such that in the given domain of variation of the variables to every pair of values $ \alpha _ {1} $ and $ \alpha _ {2} $ corresponds only one pair of values $ x $ and $ y $. The scheme of a binary field $ ( \alpha _ {1} , \alpha _ {2} ) $ is illustrated in Fig. b.
Scales, families of marked lines and binary fields are formed so that it is convenient to find points and lines with given marks and to determine the marks of answer points and lines.
Elementary nomograms are those in which the answer or answers can be found as a result of performing a single geometric operation (determining a point on a scale or in a binary field; drawing a line through two points; constructing a circle with given centre and radius; dividing a segment in a given ratio; drawing a line parallel to a given one; laying off a segment of length equal to that of a given segment; or superimposing one plane to another).
To the elementary nomograms belong: the graph of a function; scale doubling alignment; nomograms from adjusted points; nomograms from equidistant points; nomograms using a compass; nomograms with parallel indices; barycentric nomograms; rhomboidal nomograms; nomograms with an oriented transparency; and nomograms with a transparency of general form. Key
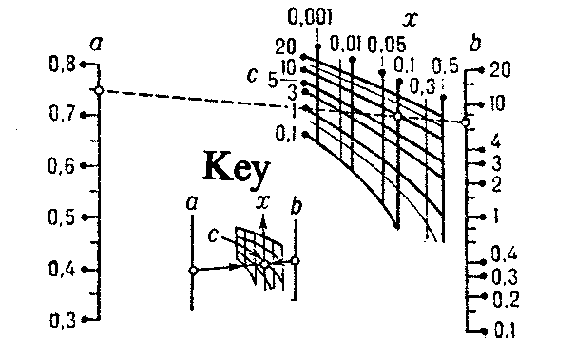
Figure: n066890c
In Fig. can elementary nomogram is drawn from adjusted points for the determination of the quantity $ x $ from the equation
$$ x ^ {a-} 1 = b \frac{ \mathop{\rm ln} ( c - x ) }{c - x - 1 } , $$
which is used for thermal calculations involving ventilators. The nomogram is constructed within the limits: $ 0 . 3 \leq a \leq 0 . 8 $; $ 0 . 1 \leq b \leq 20 $; $ 0 . 1 \leq c \leq 20 $; $ 0.001 \leq x < 0 .5 $. The variables $ a $ and $ b $ are represented on the nomogram by scales; the variables $ c $ and $ x $ by a binary field. The nomogram shows the solution of a numerical example (data: $ a = 0 . 75 $; $ b = 7 $; $ c = 10 $; answer: $ x = 0 . 1 $).
Elementary nomograms have a simple geometric foundation: the nomographic interpretation of the condition that three points are collinear leads to a nomogram from adjusted points; the formulas for the distance between two points — to a nomogram from equidistant points and to the use of a compass; the formulas for the coordinates of a point dividing a segment in a given ratio — to a barycentric nomogram; the condition that two lines are parallel — to a nomogram with parallel indices; the formulas determining the coordinates of the fourth vertex of a parallelogram from three given vertices of it — to a rhomboidal nomogram; the formulas for the transformation of rectangular coordinates with, or without, rotation of the axes — a nomogram on two planes (with an oriented transparency or of general form).
To every elementary nomogram corresponds a canonical form of dependency that can be illustrated by the nomogram. Some canonical forms allow the construction of elementary nomograms of various types.
The most general canonical form represented by an elementary nomogram of adjusted points is
$$ \frac{f _ {34} - f _ {12} }{g _ {34} - g _ {12} } = \ \frac{f _ {56} - f _ {12} }{g _ {56} - g _ {12} } . $$
The corresponding nomogram consists of three binary fields $ ( \alpha _ {1} , \alpha _ {2} ) $, $ ( \alpha _ {3} , \alpha _ {4} ) $ and $ ( \alpha _ {5} , \alpha _ {6} ) $, connected by a single alignment.
Below the frequently occurring canonical forms for individual equations and systems of equations representable by nomograms of one type or another are presented.
Canonical forms for individual equations: a) with three variables:
$$ f _ {1} = f _ {23} ,\ \ f _ {1} f _ {3} + f _ {2} g _ {3} + h _ {3} = 0 ,\ \ f _ {1} + f _ {2} = f _ {3} ,\ \ f _ {1} = f _ {2} f _ {3} ; $$
b) with four variables:
$$ f _ {12} = f _ {34} ,\ \ f _ {1} f _ {34} + f _ {2} g _ {34} + h _ {34} = 0 ,\ \ f _ {12} = f _ {3} + f _ {4} ; $$
c) with five variables:
$$ f _ {12} = f _ {34} + f _ {35} ; \ \ f _ {1} + f _ {2} + f _ {3} + f _ {4} + f _ {5} = 0 , $$
$$ f _ {5} = F ( f _ {12} + f _ {34} , g _ {12} + g _ {34} ) ; $$
d) with six variables:
$$ f _ {12} + f _ {13} = f _ {45} + f _ {46} ,\ \ f _ {1} + f _ {2} + f _ {3} + f _ {4} + f _ {5} + f _ {6} = 0 ; $$
e) with seven variables:
$$ f _ {7} = F ( f _ {12} + f _ {34} + f _ {56} , g _ {12} + g _ {31} + g _ {56} ) , $$
$$ f _ {1} + f _ {2} + f _ {3} + f _ {4} + f _ {5} + f _ {6} + f _ {7} = 0 . $$
Canonical forms for systems of equations:
$$ \left . \begin{array}{c} f _ {3} = f _ {12} , \\ g _ {4} = g _ {12} ; \end{array} \right \} \ \ \left . \begin{array}{c} f _ {12} + f _ {34} = f _ {56} , \\ g _ {12} + g _ {34} = g _ {56} ; \end{array} \right \} \ \ \left . \begin{array}{c} f _ {12} - f _ {56} = f _ {34} - f _ {56} , \\ g _ {12} - g _ {56} = g _ {34} - g _ {78} ; \end{array} \right \} $$
$$ \left . \begin{array}{c} f _ {12} - g _ {7} = f _ {34} - f _ {8} = f _ {56} - f _ {9} , \\ g _ {12} - g _ {7} = g _ {34} - g _ {8} = g _ {56} - g _ {9} . \end{array} \right \} $$
Composite nomograms consist of elementary nomograms of the same type or of several types. The introduction of composite nomograms considerably extends the class of dependencies that can be represented nomographically. For a summary of canonical forms that can be represented by elementary and composite nomograms see [3] and [4].
A dependency with three variables can always be represented nomographically. Dependencies with four or more variables allow the construction of nomograms only in special cases.
To extend the range of nomographically-representable dependencies one uses approximate representations. One such is based on allowing the given dependency to be nomographed with a certain admissible error. $ Q $, $ \textrm{ m } ^ {3} / \mathop{\rm sec} $, $ v \textrm{ m } / \mathop{\rm sec} $, data
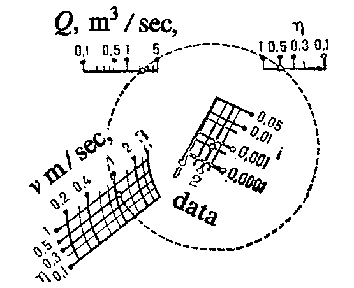
Figure: n066890d
In Fig. dan approximate nomogram from equidistant points is drawn for the determination of the quantities $ \eta $ and $ v $( or $ Q $ and $ v $) from the system of equations
$$ \left . \begin{array}{c} Q = \left ( 76 . 9 + 17 . 72 \mathop{\rm log} \frac{b \eta }{1 + 2 \eta } \right ) \frac{b ^ {2.5} \eta ^ {1.5} i ^ {0.5} }{( 1 + 2 \eta ) ^ {0.5} } , \\ v = \left ( 76 . 9 + 17 . 72 \mathop{\rm log} \frac{b \eta }{1 + 2 \eta } \right ) \frac{b ^ {0.5} \eta ^ {0.5} i ^ {0.5} }{( 1 + 2 \eta ) ^ {0.5} } , \end{array} \right \} $$
which is used for the calculation of rectangular flows in hydraulics. To use nomography this system was replaced by the approximate system
$$ Q = \ \frac{76 b ^ {2.616} \eta ^ {1.616} i ^ {0.5} }{( 1 + 2 \eta ) ^ {0.616} } ,\ \ v = \ \frac{76 b ^ {0.616} \eta ^ {0.616} i ^ {0.5} }{( 1 + 2 \eta ) ^ {0.616} } , $$
with a relative error in $ Q $ and $ v $ not exceeding $ 2 . 5\pct $. The dotted circle in the nomogram corresponds to the solution of a numerical example (data: $ i = 0 . 0005 $; $ b = 2 \textrm{ m } $; $ Q = 2 . 2 \textrm{ m } ^ {3} / \mathop{\rm sec} $; answers: $ \eta = 0 . 5 $ and $ v = 1 . 1 \textrm{ m } / \mathop{\rm sec} $).
In some cases the methods of approximate nomography make it possible to represent a table with several entries by nomograms.
To obtain the nomographic representation of a given dependency one puts it accurately or approximately into nomographic form and writes down the equations of the elements of the nomogram in a rectangular coordinate system. The transformation parameters occurring in these equations (and sometimes also arbitrary functions) are chosen so that they give to the nomogram a form convenient to use. Next one calculates tables of coordinates of the individual elements of the nomogram and then one draws the nomogram.
Machine nomography has been developed (see [4]–[6]): Systems of procedures and of standard programs have been worked out for the automatic calculation and construction of elementary nomograms by means of computers and graphical construction as well as standard programs for the automatic construction, calculation and sketching of nomograms of various types.
The main problems of theoretical nomography are representability and uniqueness. The essence of the first problem consists in clarifying whether a given equation or system of equations can be brought to some canonical form and, if possible, to determine an algorithm for this process. Solutions of this problem have been obtained for certain canonical forms. They are cumbersome and seldom used in practice. The essence of the second problem consists in finding out whether there is a unique way of bringing a given dependency to canonical form, and when it is not unique to indicate all possible ways and for each of them to establish whether the nomogram can be transformed into it.
References
| [1] | M.V. Pentkovskii, "Nomography" , Moscow-Leningrad (1949) (In Russian) |
| [2] | B.A. Neveskii, "Handbook of nomography" , Moscow-Leningrad (1951) (In Russian) |
| [3] | G.S. Khovanskii, "Eléments de nomographie" , MIR (1979) (Translated from Russian) |
| [4] | G.S. Khovanskii, "Nomography and its possibilities" , Moscow (1977) (In Russian) |
| [5] | G.S. Khovanskii (ed.) , Nomography collection , 15 , Moscow (1986) (In Russian) |
| [6] | G.S. Khovanskii, "Nomography today" , Moscow (1987) (In Russian) |
Comments
References
| [a1] | K. Rektorys (ed.) , Survey of applicable mathematics , Iliffe (1969) pp. Sect. 32A |
| [a2] | R. Sauer (ed.) I. Szabó (ed.) , Mathematische Hilfsmittel des Ingenieurs , III , Springer (1967) pp. Sect. G.I.3 |
| [a3] | D.S. Davis, "Nomography and empirical relations" , Wiley (1962) |
| [a4] | A.S. Levens, "Nomography" , Wiley (1959) |
| [a5] | L. Johnson, "Nomography and empirical equations" , Wiley (1952) |
Nomography. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nomography&oldid=47980