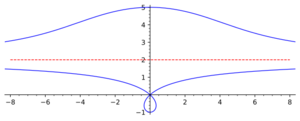
Nicomedes conchoid
A plane algebraic curve of order 4 whose equation in Cartesian rectangular coordinates has the form
$$(x^2+y^2)(x-a)^2-l^2x^2=0;$$
and in polar coordinates
$$\rho=\frac{a}{\sin\psi}\pm l.$$
Outer branch (see Fig.). Asymptote $x=a$. Two points of inflection, $B$ and $C$.
Inner branch. Asymptote $x=a$. The coordinate origin is a double point whose character depends on the values of $a$ and $l$. For $l<a$ it is an isolated point and, in addition, the curve has two points of inflection, $E$ and $F$; for $l>a$ it is a node; for $l=a$ it is a cusp. The curve is a conchoid of the straight line $x=a$.
The curve is named after Nicomedes (3rd century B.C.), who used it to solve the problem of trisecting an angle.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
Nicomedes conchoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nicomedes_conchoid&oldid=52844