Mori theory of extremal rays
Let $f : X \rightarrow S$ be a projective morphism of algebraic varieties over a field $k$ of characteristic $0$ (cf. also Algebraic variety). A relative $\mathbf{R}$-$1$-cycle is a formal linear combination $Z = \sum _ { i = 1 } ^ { t } r _ { j } C _ { j }$ of a finite number of curves $C_{j}$ (reduced irreducible $1$-dimensional closed subschemes) on $X$ with real number coefficients $r _ { j }$ such that $f ( C _ { j } )$ are points on $S$. (If $S = \operatorname{Spec} k$, then the word "relative" is dropped.) Two relative $\mathbf{R}$-$1$-cycles $Z _ { 1 }$ and $Z_2$ are said to be numerically equivalent if their intersection numbers are equal, $( D . Z _ { 1 } ) = ( D . Z _ { 2 } ) \in \bf R$ for any Cartier divisor $D$ on $X$ (cf. also Divisor; Intersection index (in algebraic geometry)). The set $N _ { 1 } ( X / S )$ of all the equivalence classes of relative $\mathbf{R}$-$1$-cycles with respect to the numerical equivalence becomes a finite-dimensional real vector space. The closed cone of curves (the Kleiman–Mori cone) $\overline { N E } ( X / S )$ is defined to be the closed convex cone in $N _ { 1 } ( X / S )$ generated by the classes of curves on $X$ which are mapped to points on $S$ by $f$. A half-line $R = {\bf R} _ { \geq 0 } v \subset \overline { N E } ( X / S )$ is called an extremal ray if the inequality $( ( K_{X} + B ) \cdot v ) < 0$ holds and if the equality $v = v _ { 1 } + v _ { 2 }$ for $v _ { 1 } , v _ { 2 } \in \overline { NE } ( X / S )$ implies $v _ { 1 } , v _ { 2 } \in R$.
Cone theorem.
Let $X$ be a normal algebraic variety and $B$ an effective $\mathbf{Q}$-divisor such that the pair $( X , B )$ is weakly log terminal (cf. Kawamata rationality theorem). Let $f : X \rightarrow S$ be a projective morphism to another algebraic variety. Then there exist at most countably many extremal rays $R _ { j } = {\bf R} _ { \geq 0 } v_j$ ($j \in J$) satisfying the following conditions:
For any $v \in \overline { N E } ( X / S )$, there exist an element $v ^ { \prime } \in \overline { N E } ( X / S )$ and numbers $r _ { j } \in {\bf R} _ { \geq 0 }$, which are zero except for finitely many $j$, such that $( ( K _ { X } + B ) \cdot v ^ { \prime } ) \geq 0$ and $v = v ^ { \prime } + \sum_j r_j v_j$.
(discreteness) For any closed convex cone $\Sigma$ in $N _ { 1 } ( X / S )$ such that $( ( K_{X} + B ) \cdot v ) < 0$ for any $v \in \Sigma \backslash \{ 0 \}$, there exist only finitely many $j \in J$ such that $v _ { j } \in \Sigma$.
Contraction theorem.
Let $R$ be an extremal ray as above. Then there exists a morphism $\phi : X \rightarrow Y$, called a contraction morphism, to a normal algebraic variety $Y$ with a morphism $g : Y \rightarrow S$ which is characterized by the following properties:
$g \circ \phi = f$;
$\phi_{*} {\cal O} _ { X } = {\cal O} _ { Y }$;
any curve $C$ which is mapped to a point by $f$ is mapped to a point by $\phi$ if and only if its numerical class belongs to $R$.
Two methods of proofs for the cone theorem are known. The first one [a6] uses a deformation theory of morphisms over a field of positive characteristic and applies only in the case where $X$ is smooth. It is important to note that this is the only known method in mathematics to prove the existence of rational curves (as of 2000). The second approach [a2] uses a vanishing theorem of cohomology groups (cf. Kawamata–Viehweg vanishing theorem) which is true only in characteristic $0$. This method of proof, which is obtained via a rationality theorem (cf. Kawamata rationality theorem), applies also to singular varieties and easily extends to the logarithmic version as explained above. The contraction theorem has been proved only by a characteristic-$0$ method (cf. [a1]).
In the following it is also assumed that the variety $X$ is $\mathbf{Q}$-factorial, that is, for any prime divisor $D$ on $X$ there exists a positive integer $m$, depending on $D$, such that $m D$ is a Cartier divisor. Then the contraction morphism $\phi$ is of one of the following types:
(Fano–Mori fibre space) 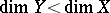 .
.
(divisorial contraction) There exists a prime divisor $E$ of $X$ such that $\operatorname{codim}\phi ( E ) \geq 2$ and $\phi$ induces an isomorphism $X\backslash E \rightarrow Y \backslash \phi ( E )$.
(small contraction) $\phi$ is an isomorphism in codimension $1$, in the sense that there exists a closed subset $E$ of codimension $\geq 2$ of $X$ such that $\phi$ induces an isomorphism $X\backslash E \rightarrow Y \backslash \phi ( E )$.
Flip conjectures.
The first flip conjecture is as follows: Let $\phi : X \rightarrow Y$ be a small contraction. Then there exists a birational morphism from a $\mathbf{Q}$-factorial normal algebraic variety $\phi ^ { + } : X ^ { + } \rightarrow Y$ which is again an isomorphism in codimension $1$ and is such that the pair $( X ^ { + } , B ^ { + } )$ with $B ^ { + } = ( \phi _ { * } ^ { + } ) ^ { - 1 } \phi_{ *} B$ is weakly log terminal and $K _ { X ^{+}} + B ^ { + }$ is a $\phi ^ { + }$-ample $\mathbf{Q}$-divisor (cf. also Divisor). The diagram $X \rightarrow Y \leftarrow X ^ { + }$ is called a flip (or log flip). Note that $- ( K _ { X } + B )$ is $\phi$-ample.
The second flip conjecture states that there does not exist an infinite sequence of consecutive flips.
There is no small contraction if $\operatorname{dim} X \leq 2$. The flip conjectures have been proved for $\operatorname { dim } X = 3$ (see [a3], [a4] for the first flip conjecture, and [a5], [a7] for the second). The proofs depend on the classification of singularities and it is hard to extend them to a higher-dimensional case.
Minimal model program (MMP).
Fix a base variety $S$ and consider a category whose objects are a pair $( X , B )$ and a projective morphism $f : X \rightarrow S$ such that $X$ is a $\mathbf{Q}$-factorial normal algebraic variety and $B$ is a $\mathbf{Q}$-divisor such that $( X , B )$ is weakly log terminal. A morphism from $( ( X , B ) , f )$ to $( ( X ^ { \prime } , B ^ { \prime } ) , f ^ { \prime } )$ in this category is a birational mapping $\alpha : X _ { .. } \rightarrow X ^ { \prime }$ which is surjective in codimension $1$, in the sense that any prime divisor on $X ^ { \prime }$ is the image of a prime divisor on $X$, and such that $B ^ { \prime } = \alpha_{*} B$ and $f ^ { \prime } \circ \alpha = f$. The minimal model program is a program which works under the assumption that the flip conjectures hold. It starts from an arbitrary object $( ( X , B ) , f )$ and constructs a morphism to another object $( ( X ^ { \prime } , B ^ { \prime } ) , f ^ { \prime } )$ such that one of the following holds:
$X ^ { \prime }$ has a Fano–Mori fibre space structure $\phi : X ^ { \prime } \rightarrow Y$ over $S$.
$X ^ { \prime }$ is minimal over $S$ in the sense that $K _ { X ^ { \prime } } + B ^ { \prime }$ is $f ^ { \prime }$-nef, i.e., an inequality $( ( K _ { X ^ { \prime } } + B ^ { \prime } ) . C ) \geq 0$ holds for any curve $C$ on $X ^ { \prime }$ such that $f ( C )$ is a point on $S$. Construct objects $( ( X _ { n } , B _ { n } ) , f _ { n } )$ inductively as follows. Set $( ( X _ { 0 } , B _ { 0 } ) , f _ { 0 } ) = ( ( X , B ) , f )$. Suppose that $( ( X _ { n } , B _ { n } ) , f _ { n } )$ has already been constructed. If $K _ { X _ { n } } + B _ { n }$ is $f _ { n }$-nef, then a minimal model is obtained. If not, then, by the cone theorem, there exists an extremal ray and one obtains a contraction morphism $\phi : X _ { n } \rightarrow Y$ by the contraction theorem. If $\operatorname { dim } Y < \operatorname { dim } X _ { n }$, then a Fano–Mori fibre space is obtained. If $\phi$ is a divisorial contraction, then one sets $( ( X _ { n + 1} , B _ { n + 1} ) , f _ { n + 1 } ) = ( ( Y , \phi_{ * } B _ { n } ) , f _ { n } \circ \phi ^ { - 1 } )$. If $\phi$ is a small contraction and if the first flip conjecture is true, then take the flip $\phi ^ { + } : X _ { n } ^ { + } \rightarrow Y$ and set $( ( X _ { n + 1 } , B _ { n + 1 } ) , f _ { n + 1 } ) = ( ( X _ { n } ^ { + } , ( \phi _ { * } ^ { + } ) ^ { - 1 } \phi _ { * } B _ { n } ) , f _ { n } \circ \phi ^ { - 1 } \circ \phi ^ { + } )$. If the second flip conjecture is true, then this process stops after a finite number of steps.
A normal algebraic variety $X$ is said to be terminal, or it is said that $X$ has only terminal singularities, if the following conditions are satisfied:
1) The canonical divisor $K _ { X }$ is a $\mathbf{Q}$-Cartier divisor.
2) There exists a projective birational morphism $\mu : Y \rightarrow X$ from a smooth variety with a normal crossing divisor $D = \sum _ { k = 1 } ^ { s } D _ { k }$ such that one can write $\mu ^ { * } K _ { X } = K _ { Y } + \sum _ { k } d _ { k } D _ { k }$ with $d _ { k } < 0$ for all $k$.
As a special case of the minimal model program, if one assumes that $X$ has only terminal singularities and $B = 0$, then any subsequent pair satisfies the same condition that $X_n$ has only terminal singularities and $B _ { n } = 0$. This is the "non-log" version.
It is expected that the minimal model program works also over a field of arbitrary characteristic, although the cone and contraction theorems are conjectural in general.
References
| [a1] | Y. Kawamata, K. Matsuda, K. Matsuki, "Introduction to the minimal model problem" Adv. Stud. Pure Math. , 10 (1987) pp. 283–360 MR0946243 Zbl 0672.14006 |
| [a2] | Y. Kawamata, "The cone of curves of algebraic varieties" Ann. of Math. , 119 (1984) pp. 603–633 MR0750714 MR0744865 Zbl 0544.14009 |
| [a3] | S. Mori, "Flip theorem and the existence of minimal models for 3-folds" J. Amer. Math. Soc. , 1 (1988) pp. 117–253 MR0924704 Zbl 0649.14023 |
| [a4] | V. Shokurov, "3-fold log flips" Izv. Russian Akad. Nauk. , 56 (1992) pp. 105–203 Zbl 0785.14023 |
| [a5] | V. Shokurov, "The nonvanishing theorem" Izv. Akad. Nauk. SSSR , 49 (1985) pp. 635–651 MR794958 |
| [a6] | S. Mori, "Threefolds whose canonical bundles are not numerically effective" Ann. of Math. , 116 (1982) pp. 133–176 Zbl 0557.14021 Zbl 0493.14020 |
| [a7] | Y. Kawamata, "Termination of log-flips for algebraic 3-folds" Internat. J. Math. , 3 (1992) pp. 653–659 MR1189678 Zbl 0814.14016 |
Mori theory of extremal rays. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mori_theory_of_extremal_rays&oldid=55369