Monogenic function
A function of a complex variable having a finite derivative. More precisely, a function $ f ( z) $
defined on a set $ E $
of the complex plane $ \mathbf C $
is called monogenic (with respect to $ E $)
at a finite non-isolated point $ \zeta \in E $
if it has a finite derivative $ f _ {E} ^ { \prime } ( \zeta ) $
with respect to $ z \in E $
at this point:
$$ f _ {E} ^ { \prime } ( \zeta ) = \ \lim\limits _ {\begin{array}{c} z \rightarrow \zeta \\ z \in E \end{array} } \ \frac{f ( z) - f ( \zeta ) }{z - \zeta } . $$
A function which is monogenic at every non-isolated point of $ E $ is called monogenic on $ E $.
If $ E = G $ is a domain in $ \mathbf C $, then a monogenic function on $ G $ is called an analytic function on $ G $.
If $ E $ is not a domain, then a monogenic function on $ E $, in general, will no longer have the typical properties of an analytic function. However, if a set $ E $, which itself is not a domain, is sufficiently "massive" near a majority of its points (more precisely, if the complement of $ E $ in $ \mathbf C $ is sufficiently thin near a majority of $ \zeta \in E $), then a monogenic function on $ E $ has, in a weakened form, many of the properties of an analytic function. In attempts to gain a deep understanding of connections between properties of analytic functions, the notion of an analytic function has been generalized in various directions: by generalizing the domain of definition, by generalizing the very notion of the derivative itself, by weakening the Cauchy–Riemann conditions, by weakening the condition of Morera's theorem, etc. (see [13], Chapt. 6). To this end, for "thin" sets $ E $, for example, for a segment $ E = [ a , b ] \subset ( - \infty , \infty ) $, the so-called quasi-analytic classes (cf. Quasi-analytic class) of functions have been picked out. Functions defined on nowhere-dense sufficiently massive compact sets $ E $, which are close to analytic functions in the sense that they can be uniformly approximated to any accuracy by analytic functions, or, what is the same thing, by rational functions of $ z $, have also been studied.
Below some results in the areas listed are given.
1. Functions monogenic in a domain.
If $ f ( z) = f ( x + i y ) = u ( x , y ) + i v ( x , y ) $( here $ u ( x , y ) $ and $ v ( x , y ) $ are real-valued functions), then for $ f ( z) $ to be analytic in a domain $ G $ it is sufficient (and necessary) that at every point $ x + i y \in G $ the following two conditions are simultaneously satisfied: 1) $ u ( x , y ) $ and $ v ( x , y ) $ have total differentials $ d u ( x , y ) $ and $ d v ( x , y ) $ with respect to the set of real variables $ ( x , y ) $; and 2) the Cauchy–Riemann conditions are satisfied:
$$ \frac{\partial u ( x , y ) }{\partial x } = \ \frac{\partial v ( x , y ) }{\partial y } ,\ \ \frac{\partial u ( x , y ) }{\partial y } = - \frac{\partial v ( x , y ) }{\partial x } . $$
The conditions of this theorem can be weakened and generalized. For example, it has been shown that the requirement of existence of the total differentials for $ u $ and $ v $ can be replaced by the essentially weaker condition of boundedness of $ u $ and $ v $ in $ G $ and, while preserving the requirement of the existence of the first partial derivatives of $ u $ and $ v $ everywhere in $ G $, requiring only that the Cauchy–Riemann equations be satisfied almost-everywhere in $ G $( in the sense of the Lebesgue measure in the plane) (see [6]).
Let $ L ( z) $ be any pair of distinct lines intersecting at $ z $, let $ R ( z) $ be any triple of pairwise non-collinear rays emanating from $ z $ and let $ E ( z) $ be any measurable set having $ z $ as a Lebesgue density point. Analyticity of a continuous function $ f ( z) $ in $ G $ is guaranteed by each of the following conditions individually (see [3]–[5]): a) $ f _ {L(} z) ^ { \prime } \neq \infty $ exists everywhere in $ G $; b) $ f _ {R(} z) ^ { \prime } \neq \infty $ exists everywhere in $ G $; or c) $ f _ {E(} z) ^ { \prime } \neq \infty $ exists everywhere in $ G $. Here each of the sets $ L ( z) $, $ R ( z) $ and $ E ( z) $ has its own definition at each point. It must be noted that $ f _ {E(} z) ^ { \prime } ( z) $ depends on $ f $ and $ z $ but not on $ E ( z) $; the derivative
$$ f _ {as} ^ { \prime } ( z) = \ f _ {E(} z) ^ { \prime } ( z) $$
is called an asymptotic (approximate) derivative, and a function having a asymptotic derivative at a point $ z $( respectively, in a domain $ G $) is called asymptotically monogenic at $ z $( in $ G $). Instead of condition b) it suffices to require the existence of a limit for
$$ \mathop{\rm arg} \ \frac{f ( z ^ \prime ) - f ( z) }{z ^ \prime - z } \ \ \textrm{ as } \ z ^ \prime \rightarrow z ,\ \ z ^ \prime \in R ( z) . $$
2. Functions monogenic on nowhere-dense sets.
E. Borel [8] constructed a connected perfect set (a continuum) $ E $ without interior points and an increasing sequence $ E _ {1} \subset E _ {2} \subset \dots \subset E $ of perfect sets such that the area $ \mathop{\rm mes} _ {2} E $ of $ E $ is positive,
$$ \mathop{\rm mes} _ {2} \ \left ( E \setminus \cup _ { n= } 1 ^ \infty E _ {n} \right ) = 0 , $$
and such that monogeneity of $ f ( z) $ on $ E $( or even on each set $ E _ {n} $, $ n = 1 , 2 ,\dots $) implies that $ f ( z) $ is infinitely differentiable with respect to $ z \in E _ {n _ {0} } $ for each fixed $ n _ {0} $. One could give comparatively general sufficient conditions on $ E $ so that $ f ( z) $ has this property, or the weaker property of $ k $ times differentiability with respect to $ z \in E _ {n} $, where $ k $ is a natural number given in advance. Sufficient conditions on the nowhere-dense continuum $ E $ have also been found so that for monogenic functions on it, analogues of Cauchy's integral theorem, Taylor series expansions and various forms of uniqueness theorems hold. One example of the latter: If two monogenic functions $ f _ {1} ( z) $ and $ f _ {2} ( z) $ on $ E $ coincide on some portion of $ E $( that is, on the non-empty intersection of $ E $ with an open disc), then $ f _ {1} ( z) \equiv f _ {2} ( z) $ on $ E $( see [9]).
3. Functions close to analytic functions.
As is well known, any function $ f ( z) $ that is analytic in a domain $ G $ is the limit of a sequence of rational functions $ r _ {n} ( z) $ which converge to $ f ( z) $ uniformly on each compact set $ K \subset G $. If one considers a sufficiently massive nowhere-dense continuum $ E $ and the class $ R ( E) $ of functions $ f ( z) $, $ z \in E $, for which there is a sequence of rational functions $ r _ {n} ( z , f ) $ uniformly converging to $ f ( z) $, then one obtains yet another generalization of the notions of a domain and a function $ f ( z) $ analytic on $ E $. If $ E $ is a nowhere-dense set in $ \mathbf C $, then one can always find a function $ f \in R ( E) $ not having a derivative $ f _ {E} ^ { \prime } ( z) $ at any $ z \in E $( see [10]). However, for every $ m $, $ 2 \leq m \leq \infty $, it is possible to give conditions on $ E $ under which every $ f \in R ( E) $ has derivatives $ f _ {E _ {n} } ^ { ( k) } ( z) $, where $ 1 \leq k < m $, where $ E _ {n} $ is closed, $ E _ {n} \subset E $ and $ \mathop{\rm mes} _ {2} ( E \setminus E _ {n} ) < 1 / n $( see [11]). M.V. Keldysh has constructed an example of a nowhere-dense continuum $ E $ on which the uniqueness theorem in the form quoted at the end of Subsection $ \mathbf 2 $ holds for functions $ f _ {1} , f _ {2} \in R ( E) $( see also [12]). (Concerning the monogenic properties of functions from $ R ( E) $ in terms of functional analysis see [12], Chapt. I, Sect. 17.) The dependence of the monogenic properties of a function $ f \in R ( E) $ on the speed of its approximation by rational functions has also been investigated.
References
| [1] | V.S. Fedorov, "The work of N.N. Luzin on the theory of functions of a complex variable" Uspekhi Mat. Nauk , 7 : 2 (1952) pp. 7–16 (In Russian) |
| [2] | H. Bohr, "Ueber streckentreue und konforme Abbildung" Math. Z. , 1 (1918) pp. 403–420 |
| [3] | D.E. Men'shov, "Sur la généralisation des conditions de Cauchy–Riemann" Fund. Math. , 25 (1935) pp. 59–97 |
| [4] | D.E. Men'shov, "Les conditions de monogénéité" , Hermann (1936) |
| [5] | D.E. Men'shov, "On asymptotic monogeneity" Mat. Sb. , 1 (1936) pp. 189–210 (In Russian) |
| [6] | G.P. Tolstov, "On curvilinear and repeated integrals" Trudy Mat. Inst. Steklov. , 35 (1950) (In Russian) |
| [7] | Yu.Yu. Trokhimchuk, "Continuous mappings and monogeneity conditions" , Moscow (1963) (In Russian) |
| [8] | E. Borel, "Leçons sur les fonctions monogènes uniformes d'une variable complexe" , Gauthier-Villars (1917) |
| [9] | A.I. Seleznev, "On functions monogenic on nowhere closed sets and sets of type 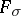 " Dokl. Akad. Nauk SSSR , 108 : 4 (1956) pp. 591–594 (In Russian) " Dokl. Akad. Nauk SSSR , 108 : 4 (1956) pp. 591–594 (In Russian) |
| [10] | E.P. Dolzhenko, "Construction on a nowhere dense continuum of a nowhere differentiable function which can be expanded in a series of rational functions" Dokl. Akad. Nauk SSSR , 125 : 5 (1959) pp. 970–973 (In Russian) |
| [11] | E.P. Dolzhenko, "Approximation on closed regions and zero-sets" Soviet Math. Dokl. , 3 : 2 (1962) pp. 472–475 Dokl. Akad. Nauk SSSR , 143 : 4 (1962) pp. 771–774 |
| [12] | M.S. Mel'nikov, S.O. Sinanyan, "Aspects of approximation theory for functions of one complex variable" J. Soviet Math. , 5 : 5 (1976) pp. 688–752 Itogi Nauk. i Tekhn. Sovrem. Probl. Mat. , 4 (1975) pp. 143–250 |
| [13] | A.F. Bermant, A.I. Markushevich, "Theory of functions of a complex variable" , Mathematics in the USSR during thirty years: 1917–1947 , Moscow-Leningrad (1948) pp. 319–481 (In Russian) |
| [14] | D.S. Telyakovskii, "Generalization of the Looman–Men'shov theorem" Math. Notes , 19 : 4 (1986) pp. 296–301 Mat. Zametki , 39 : 4 (1986) pp. 539–549 |
Monogenic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Monogenic_function&oldid=47887