Modules, category of
The category mod- $ R $
whose objects are the right unitary modules over an arbitrary associative ring $ R $
with identity, and whose morphisms are the homomorphisms of $ R $-
modules. This category is the most important example of an Abelian category. Moreover, for every small Abelian category there is a full exact imbedding into some category of modules.
If $ R = \mathbf Z $, the ring of integers, then mod- $ R $ is the category of Abelian groups, and if $ R = D $ is a skew-field, then mod- $ R $ is the category of vector spaces over $ D $.
The properties of mod- $ R $ reflect a number of important properties of the ring $ R $( see Homological classification of rings). Connected with this category is a number of important homological invariants of the ring; in particular, its homological dimension. The centre of mod- $ R $( that is, the set of natural transformations of the identity functor of the category) is isomorphic to the centre of $ R $.
In ring theory, homological algebra and algebraic $ K $- theory, various subcategories of the category of modules are discussed; in particular, the subcategory of finitely-generated projective $ R $- modules and the associated $ K $- functors (see Algebraic $ K $- theory). By analogy with Pontryagin duality, dualities between full subcategories of the category of modules have been studied; in particular between subcategories of finitely-generated modules. For example, it has been established that if $ R $ and $ S $ are Noetherian rings and if there is duality between finitely-generated right $ R $- modules and finitely-generated left $ S $- modules, then there is a bimodule $ {} _ {S} U _ {R} $ such that the given duality is equivalent to the duality defined by the functors
$$ \mathop{\rm Hom} _ {R} ( - , U ) \ \ \textrm{ and } \ \ \mathop{\rm Hom} _ {S} ( - , U ) , $$
the ring of endomorphisms $ \mathop{\rm End} U _ {R} $ is isomorphic to $ S $, $ \mathop{\rm End} {} _ {S} U $ is isomorphic to $ R $, the bimodule $ U $ is a finitely-generated injective cogenerator (both as an $ R $- module and an $ S $- module), and the ring $ R $ is semi-perfect (cf. Semi-perfect ring). The most important class of rings, arising in the consideration of duality of modules, is the class of quasi-Frobenius rings (cf. Quasi-Frobenius ring). A left Artinian ring $ R $ is quasi-Frobenius if and only if the mapping
$$ M \rightarrow \mathop{\rm Hom} _ {R} ( M , R ) $$
defines a duality between the categories of finitely-generated left and right $ R $- modules.
References
| [1] | H. Bass, "Algebraic 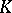 -theory" , Benjamin (1968) MR249491 -theory" , Benjamin (1968) MR249491 |
| [2] | I. Bucur, A. Deleanu, "Introduction to the theory of categories and functors" , Wiley (1968) MR0236236 Zbl 0197.29205 |
| [3] | C. Faith, "Algebra: rings, modules and categories" , 1–2 , Springer (1973–1976) MR0551052 MR0491784 MR0366960 Zbl 0508.16001 Zbl 0266.16001 |
Comments
A duality given by a bimodule $ U $ as described above is called a $ U $- duality or Morita duality; cf. also (the comments to) Morita equivalence.
Modules, category of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Modules,_category_of&oldid=47874