Mixed-type differential equation
A partial differential equation which is of varying type (elliptic, hyperbolic or parabolic) in its domain of definition. A linear (or quasi-linear) differential equation of the second order with two unknown variables,
$$ \tag{1 } A u _ {xx} + 2 B u _ {xy} + C u _ {yy} = \ f ( x , y , u , u _ {x} , u _ {y} ) $$
and with coefficients defined in the domain $ \Omega $ is an equation of mixed type if the discriminant $ \Delta = A C - B ^ {2} $ of the characteristic form
$$ A d y ^ {2} + 2 B d x d y + C d x ^ {2} = Q $$
takes the value zero in $ \Omega $ but is not identically zero there.
The curve $ \delta $ defined by the equation $ \Delta = 0 $ is called the parabolic line of equation (1) or the line of degeneracy (change) of type.
If $ \Delta $ does not change sign when the point $ ( x , y ) $ crosses the parabolic line $ \delta $ in $ \Omega $, then equation (1) is a degenerate equation of elliptic-parabolic $ ( \Delta \geq 0 ) $ or hyperbolic-parabolic $ ( \Delta \leq 0 ) $ type (see Degenerate partial differential equation).
Under certain smoothness conditions on $ A $, $ B $, $ C $, and $ \delta $, there is a non-singular real transformation of the independent variables sending equation (1) (in the case where the sign of $ \Delta $ alternates in the neighbourhood of a chosen point of $ \delta $ where $ A ^ {2} + B ^ {2} \neq 0 $) to one of the following canonical forms (the notation for the independent variables is preserved):
$$ \tag{2 } y ^ {2m+1} u _ {xx} + u _ {yy} = \ F ( x , y , u , u _ {x} , u _ {y} ) , $$
$$ \tag{3 } u _ {xx} + y ^ {2m+1} u _ {yy} = F ( x , y , u , u _ {x} , u _ {y} ) . $$
The equations (2) and (3) are equations of mixed (elliptic-hyperbolic) type in any domain containing a segment of the line of degeneracy $ y = 0 $.
The domain $ \Omega $ of definition of an equation of mixed type is sometimes called a mixed domain, and boundary value problems in mixed domains are called mixed boundary value problems. The part $ \Omega ^ {+} $ ($ \Omega ^ {-} $) of a mixed domain $ \Omega $ where the equation is of elliptic (hyperbolic) type is called the domain of ellipticity (hyperbolicity).
Many problems of an applied nature reduce to finding specific solutions of equations of mixed type; in particular, problems of plane transonic flow of a compressible medium, and problems in the theory of envelopes.
An equation (1) of mixed type is called an equation of the first kind (second kind) if the characteristic form $ Q \neq 0 $ ($ Q = 0 $) everywhere on the parabolic line. The Chaplygin equation
$$ \tag{4 } k ( y) u _ {xx} + u _ {yy} = 0 , $$
where $ k ( y) $ is a continuously-differentiable monotone function such that $ y k ( y) > 0 $ when $ y \neq 0 $, is a typical example of an equation of mixed type of the first kind. When $ k ( y) = y $, equation (4) is usually called the Tricomi equation.
An important model for an equation of mixed type (with a discontinuous coefficient in front of one of the higher derivatives) is the equation of Lavrent'ev–Bitsadze
$$ \tag{5 } ( \mathop{\rm sign} y ) \cdot u _ {xx} + u _ {yy} = 0 . $$
One of the basic boundary value problems for equations of mixed type (of the first kind) is the Tricomi problem, which is as follows for an equation of the form (2). Let $ \Omega $ be a finite simply-connected domain in the Euclidean plane with independent variables $ x $ and $ y $, bounded by a simple Jordan curve $ \sigma $ with end points $ A ( 0 , 0 ) $, $ B ( 1 , 0 ) $ lying in the half-plane $ y > 0 $, and by the parts $ A C $ and $ B C $ of the characteristics of equation (2) going through the point $ C ( 1/2 , y _ {C} ) $, $ y _ {C} < 0 $. The Tricomi problem is to find a solution $ u ( x , y ) $ of equation (2) that is continuous in the closure $ \overline \Omega \; $ of $ \Omega $ and takes given values on the curve $ \sigma \cup A C $.
In the theory of the Tricomi problem, an essential role is played by the Bitsadze extremum principle, which, in the case of equation (5), states that a solution $ u ( x , y ) $ of equation (5) in the class $ C ( \overline \Omega ) \cap C ^ {1} ( \Omega ) $ which vanishes on the characteristic $ A C $: $ x + y = 0 $, $ 0 \leq x \leq 1/2 $, in the closure $ \overline \Omega ^ {+} $ of the domain of ellipticity $ \Omega ^ {+} = \Omega \cap \{ y > 0 \} $, attains its extremum on the curve $ \sigma $.
This principle, which guarantees the uniqueness and stability of a solution of the Tricomi problem (and also provides a basic estimate to prove existence by the alternating method), can be generalized to a very wide class of linear and quasi-linear equations of mixed type. In particular, it applies to Chaplygin equations (and Tricomi equations) whenever $ k ( y) $ is twice continuously differentiable and $ 5 k ^ {\prime 2 } \geq 4 k k ^ \prime $ for $ y < 0 $. The Bitsadze extremum principle also holds for the equation
$$ \tag{6 } \mathop{\rm sign} y \cdot | y | ^ \alpha u _ {xx} + u _ {yy} = 0 , \alpha = \textrm{ const } > 0 . $$
The solution of the Tricomi problem for equation (6) in the corresponding mixed domain $ \Omega $ can be written in explicit form when the elliptic part $ \sigma $ of the boundary of this domain coincides with the so-called normal contour $ \sigma _ {0} $:
$$ x ^ {2} + \left ( \frac{2}{\alpha + 2 } \right ) ^ {2} y ^ {\alpha + 2 } = \frac{1}{4} . $$
In the general case, under specific conditions on the curve $ \sigma $ and on the class in which the solutions are sought, the Tricomi problem for equation (6) reduces to an equivalent singular integral equation which is (by virtue of the uniqueness condition) unconditionally solvable. The method of integral equations can also be applied to prove existence of a solution of the Tricomi problem, and of other mixed problems, for more general equations of the form
$$ \mathop{\rm sign} y \cdot | y | ^ \alpha u _ {xx} + u _ {yy} = F ( x , y , u , u _ {x} , u _ {y} ) $$
with power degeneracy of order $ \alpha $.
Function-theoretical methods and functional analysis, in particular the use of a priori estimates, have made it possible to extend significantly the class of equations of mixed type and mixed domains for which existence and uniqueness of a (generalized) solution can be proved, both for the Tricomi problems and for various other mixed problems.
An important generalization of the Tricomi problem is the general mixed Bitsadze problem, which, in the case of equation (5), can be posed as follows. Let $ \Omega $ be a simply-connected mixed domain bounded by a simple Jordan curve $ \sigma $ lying in the half-plane $ y > 0 $ with end points $ A ( 0 , 0 ) $, $ B ( 1 , 0 ) $ and (smooth) monotone curves $ \Gamma _ {0} $ and $ \Gamma _ {1} $ through these points, meeting at a point $ C ( x _ {1} , y _ {1} ) $, $ y _ {1} < 0 $. It is assumed that $ \Gamma _ {0} $ and $ \Gamma _ {1} $ lie in the domain bounded by the characteristics $ x + y = 0 $, $ x - y = 1 $ and the interval $ A B $: $ 0 \leq x \leq 1 $ on the $ x $-axis. Let $ B _ {0} $ and $ B _ {1} $ denote the points of intersection of the characteristics $ x - y = x _ {0} $ and $ x + y = x _ {0} $ with the curves $ \Gamma _ {0} $ and $ \Gamma _ {1} $, where $ x _ {0} $ is any fixed point of the semi-interval $ x _ {1} + y _ {1} < x _ {1} \leq x _ {1} - y _ {1} $, and let $ \gamma _ {0} $ and $ \gamma _ {1} $ denote the parts of $ \Gamma _ {0} $ and $ \Gamma _ {1} $ lying between $ A , B _ {0} $, and $ B , B _ {1} $, respectively. The general mixed Bitsadze problem consists of finding a regular solution (when $ y \neq 0 $, $ x \pm y \neq x _ {0} $) of equation (5) in $ \Omega $ which is continuous in $ \overline \Omega \; $, has continuous first derivatives in $ \Omega $ when $ x = - y \neq x _ {0} $, and satisfies given boundary conditions on $ \sigma $, $ \gamma _ {0} $ and $ \gamma _ {1} $. The uniqueness and existence of a solution of this problem, both for equation (5) and for more general equations, can be proved under certain geometric conditions on the boundary of $ \Omega $, especially on the curve $ \sigma $. The general mixed Bitsadze problem can be regarded as completely solved in the special case when $ \Gamma _ {1} $ coincides $ ( x _ {0} = 1 ) $ with the characteristic $ B C $ through the point $ B $. An important consequence of the fact that the general mixed Bitsadze problem is correctly posed, in the case of equation (5) for example, is that the Dirichlet problem for mixed domains of the form $ \Omega $ is incorrectly posed, whatever the size and form of the domain $ \Omega ^ {-} $ of hyperbolicity.
For a fairly large class of linear equations
$$ k ( y) u _ {xx} + u _ {yy} + a u _ {x} + b u _ {y} + c u = f $$
it is known that the coefficient $ a ( x , y ) $ has a substantial influence on the correctness of posing the Dirichlet problem in corresponding mixed domains of the form $ \Omega $.
Another type of mixed problem is the Frankl problem. Let $ \Omega $ be a simply-connected domain with the following boundary: the interval $ A ^ \prime A $: $ - 1 \leq y \leq 1 $ of the line $ x = 0 $, a smooth curve $ \sigma $ with end points at $ A ( 0 , 1 ) $ and $ B ( a , 0 ) $ and lying in the quadrant $ x > 0 , y > 0 $, the interval $ C B $: $ a _ {1} \leq x \leq a $ of the line $ y = 0 $, and the characteristic through $ A ^ \prime ( 0 , - 1 ) $ and $ C ( a _ {1} , 0 ) $ of the equation of mixed type under consideration (e.g. equation (4)). The Frankl problem consists of finding a solution $ u ( x , y ) $ of the equation of mixed type in $ \Omega $, given the value of $ u ( x , y ) $ on $ \sigma \cup C B $ and the conditions
$$ \frac{\partial u }{\partial x } = 0 ,\ \ u ( 0 , y ) - u ( 0 , - y ) = f ( y) , $$
$$ - 1 \leq y \leq 1 ,\ x = 0 , $$
on $ A ^ \prime A $. This problem has been investigated chiefly for model equations of mixed type and has been completely solved for equation (5) in the case where the curve $ \sigma $: $ x= x ( s) , y = y ( s) $ is such that $ d y / d s \geq 0 $, where $ s $ is the arc length of $ \sigma $ measured from the point $ B ( a , 0 ) $.
Basic boundary value problems have been formulated for equations of mixed type of the first kind and, adapted with appropriate modifications, for equations of mixed type of the second kind. These modifications are necessary because the Dirichlet problem for elliptic equations with characteristic degeneracy is not always correctly posed.
In the formulation of the boundary value problems for equation (1) in mixed domains, a new aspect is introduced if the line $ \delta $ of change of type is also a line of degeneracy of the order of equation, which occurs, for example, in the case of the equation
$$ \tag{7 } y ^ {2p} u _ {xx} + yu _ {yy} + \beta u _ {y} = 0 , $$
where $ p $ is a natural number and $ \beta $ is a constant such that $ 1 - 2 p \leq 2 \beta < 1 $.
For equations (5), (6), (7), there are, in addition to the above, a number of essentially new boundary value problems. These are chiefly characterized by the fact that the entire boundary $ \sigma \cup A C \cup B C $ of $ \Omega $ (where the Tricomi problem is posed) carries the following boundary conditions: the Dirichlet conditions, for example, on $ \Sigma $ and on $ A C \cup B C $, with some non-local condition pointwise connecting the values of the desired solution or a (fractional) derivative of it of a certain order. In particular, these problems include a simple example of a correctly-posed self-adjoint mixed boundary value problem.
Boundary value problems have also been studied for equations (and systems) of mixed type in domains containing in their interiors several lines of degeneracy of type, or one single closed parabolic line.
Analogues of the Tricomi problem have been studied for certain classes of equations and systems of mixed type in two independent variables, and for equations of higher order.
Significant difficulties arise in the search for well-posed problems for equations of mixed type with many variables. Nevertheless, several important results have been obtained also in this direction. For the equation
$$ \tag{8 } ( \mathop{\rm sign} z ) \cdot u _ {xx} + u _ {yy} + u _ {zz} = \ f ( x , y , z ) , $$
which is a simple model of an equation of mixed type having $ z = 0 $ as a time-like plane of degeneracy of type, the following problem is known to be correctly posed. Let $ \Omega $ be a finite simply-connected three-dimensional domain, bounded by a piecewise smooth surface $ z = f ( x , y ) \geq 0 $ and by the characteristic surfaces
$$ S _ {1} : x + x _ {0} = \sqrt {y ^ {2} + z ^ {2} } , $$
$$ S _ {2} : x - x _ {0} = \sqrt {y ^ {2} + z ^ {2} } $$
of equation (8). One has to find a continuously differentiable function in $ \Omega $, satisfying equation (8) in $ \Omega $ for $ z \neq 0 $, that vanishes on $ \sigma $ and on one of the characteristic surfaces $ S _ {1} $, $ S _ {2} $. Existence of a weak solution and uniqueness of a strong solution for this problem have been proved for the more general equation
$$ ( \mathop{\rm sign} x _ {n} ) \cdot u _ {x _ {n} x _ {n} } + \Delta _ {x} u = f ( x _ {0} , x ) ,\ x = ( x _ {1} \dots x _ {n} ) , $$
where $ \Delta _ {x} $ is the Laplace operator in the variables $ x _ {1} \dots x _ {n} $.
For the equation
$$ \tag{9 } x _ {0} ^ {2m} \Delta _ {x} u - x _ {0} u _ {x _ {0} x _ {0} } + \left ( m - \frac{1}{2} \right ) u _ {x _ {0} } = 0 $$
with part of the space-like hyperplane of degeneracy both of type and of order $ x = 0 $ contained in the mixed domain $ \Omega $, boundary value problems of a special form have been studied. Here the part of $ \partial \Omega $ lying in the half-space $ x _ {0} < 0 $ carries data $ u ( x _ {0} , x ) $, and the part lying in the half-space $ x _ {0} > 0 $ (the characteristic conoid of equation (9)) carries certain integral averages of $ u ( x _ {0} , x ) $.
Other model equations of mixed type in bounded and unbounded three-dimensional domains have been studied, including the equations
$$ z ^ {2m+1} u _ {xx} + u _ {yy} + u _ {zz} = 0 , $$
$$ z ^ {2m+1} ( u _ {xx} + u _ {yy} ) + u _ {zz} = 0 . $$
There is also a uniqueness criterion of the solution of the Dirichlet problem for a large class of self-adjoint equations of mixed type in cylindrical domains.
References
| [1] | L. Bers, "Mathematical aspects of subsonic and transonic gas dynamics" , Wiley (1958) |
| [2] | A.V. Bitsadse, "Equations of mixed type" , Pergamon (1964) (Translated from Russian) |
| [3] | A.V. Bitsadze, "On the theory of equations of mixed type whose order is degenerate on the line of change of type" , Continuum mechanics and related problems of analysis , Moscow (1972) pp. 47–52 (In Russian) |
| [4] | A.V. Bitsadze, A.M. Nakhusev, "Correct formulation of problems for equations of mixed type in multidimensional domains" Soviet Math. Dokl. , 13 : 4 (1972) pp. 857–860 Dokl. Akad. Nauk. SSSR , 205 : 1 (1972) pp. 9–12 |
| [5] | I.N. Vekua, "Generalized analytic functions" , Pergamon (1962) (Translated from Russian) |
| [6] | G.D. Karatopakliev, "A class of equations of mixed type" Diff. Equations , 5 : 1 (1969) pp. 171–176 Differentsial'nye Uravn. , 5 : 1 (1969) pp. 199–205 |
| [7] | M.V. Keldysh, "On certain cases of degeneracy on the boundary of a domain for equations of elliptic type" Dokl. Akad. Nauk SSSR , 77 (1951) pp. 181–183 (In Russian) |
| [8] | M.S. Salakhitdinov, "Certain boundary value problems for equations of mixed type" Izv. Akad. Nauk UzbSSR, Ser. Fiz.-Mat. Nauk , 1 (1969) pp. 27–33 (In Russian) |
| [9] | M.M. Smirnov, "Equations of mixed type" , Amer. Math. Soc. (1978) (Translated from Russian) |
| [10] | A.P. Soldatov, "A problem in function theory" Diff. Equations , 9 : 2 (1973) pp. 248–253 Differentsial'nye Uravn. , 9 : 2 (1973) pp. 325–332 |
| [11] | F. Tricomi, Atti Accad. Naz. Lincei, Ser. 5 , 14 (1932) pp. 134–247 |
| [12] | F.I. Frankl, "Selected work on gas dynamics" , Moscow (1973) (In Russian) |
| [13] | K.O. Friedrichs, "Symmetric positive linear differential equations" Comm. Pure Appl. Math. , 11 (1958) pp. 333–418 |
| [14] | S. Gellerstedt, "Quelques problèmes mixtes pour l'équation 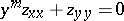 " Ark. Mat. Astr. Fysik , 26A : 3 (1937) pp. 1–32 " Ark. Mat. Astr. Fysik , 26A : 3 (1937) pp. 1–32 |
| [15] | P. Germain, R. Bader, "Sur le problème de Tricomi" C.R. Acad. Sci. Paris , 232 (1951) pp. 463–465 |
Comments
More recent workers tend to favour functional-analytic methods, see [a1]. For a constructive approach, using Fourier integral operator methods, see [a2].
References
| [a1] | M. Schneider, "Ueber Differentialgleichungen zweiter Ordnung vom gemischten Typ im 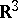 " Math. Nachr. , 66 (1975) pp. 57–66 " Math. Nachr. , 66 (1975) pp. 57–66 |
| [a2] | R.J.P. Groothhuizen, "Mixed elliptic-hyperbolic partial differential operators: a case-study in Fourier integral operators" , CWI Tracts , 16 , CWI , Amsterdam (1985) (Thesis Free University Amsterdam) |
Mixed-type differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mixed-type_differential_equation&oldid=52113