Metric theory of numbers
The branch of number theory which studies and metrically (that is, based on measure theory) characterizes sets of numbers with fixed arithmetic properties. Metric number theory is closely connected with probability theory, which sometimes proves an opportunity to use its methods and results in the analysis of number-theoretic models.
Many problems touching on arithmetic properties of individual numbers also have a metric formulation; for example, alongside questions on the uniform distribution of the sequence of fractional parts $ \{ \alpha n \} $, $ n = 1 , 2 \dots $ for $ \alpha = \sqrt 2 $ or $ \mathop{\rm log} 3 $, it is possible to pose the question: What is the Lebesgue measure of those $ \alpha $ from $ ( 0, 1) $ for which this sequence is uniformly distributed? Such a metric generalization of a problem often turns out to be very useful and provides an opportunity to represent a phenomenon in the large. Sometimes one can fairly easily prove, based on metric arguments, the existence of numbers with definite arithmetic properties, whereas a direct construction of these numbers is complicated (Borel normal numbers, cf. Normal number, numbers with certain approximation properties, etc.).
The most significant achievements in metric number theory are related to the metric theory of Diophantine approximation (cf. Diophantine approximation, metric theory of), to the theory of uniform distribution of sequences of numbers, to the theory of continued fractions (cf. Continued fraction), and to other branches of number theory.
One of the first theorems in metric number theory is Borel's theorem (E. Borel, 1909): When written in an arbitrary fixed integer base $ g $, almost-all (in the sense of Lebesgue measure) real numbers $ \alpha $ in the interval $ ( 0 , 1) $ are normal (cf. Normal number). In an equivalent formulation, this theorem asserts that the fractional parts $ \{ \alpha g ^ {n} \} $, $ n = 1 , 2 \dots $ are uniformly distributed in the interval $ ( 0 , 1 ) $. Borel's theorem has been generalized and extended by many mathematicians. It turned out to be fruitful to take the view that the "digits" $ 0 \dots g - 1 $ in the base $ g $ expansion of $ \alpha $( in the $ g $- ary system) are independent random variables. Founded explicitly or implicitly on this situation, and by applying methods developed in probability theory for finding the asymptotic distributions of sums of independent or weakly-dependent random variables, the basic questions regarding the distribution of the "digits" $ 0 \dots g - 1 $, and arbitrary groups of "digits" , in the $ g $- ary expansion of numbers "randomly" chosen from $ ( 0 , 1 ) $, were solved. For example, putting
$$ \alpha = \ \frac{a _ 1}{g} + \frac{a _ 2}{g ^ {2}} + \dots , $$
where the $ a _ {i} $ are numbers from $ 0 \dots g - 1 $, it turns out that $ a _ {i} = a _ {i} ( \alpha ) $ can be considered as independent random variables defined on $ ( 0 , 1 ) $ with the Lebesgue measure as probability measure. If $ a $ is any number from $ 0 \dots g - 1 $, and $ k _ {n} ( \alpha ) $ denotes the number of $ i \leq n $ for which $ a _ {i} ( \alpha ) = a $ for a given $ \alpha $, then
$$ \frac{( k _ {n} ( \alpha ) - n / g ) g }{\sqrt {n ( g - 1 ) } } $$
is asymptotically normally distributed, that is, for any real $ x $ the measure of the set of $ \alpha $' s for which
$$ k _ {n} ( \alpha ) - \frac{n}{g} < \ \frac{x}{g} \sqrt {n ( g - 1 ) } $$
tends, as $ n \rightarrow \infty $, to the limit
$$ \frac{1}{\sqrt {2 \pi } } \int\limits _ {- \infty } ^ { x } e ^ {- t ^ {2} /2 } d t . $$
H. Weyl (1916) proved that if $ a _ {n} $, $ n = 1 , 2 \dots $ is an arbitrary increasing sequence of natural numbers, then for almost-all $ \alpha $ the fractional parts $ \{ \alpha a _ {n} \} $ are uniformly distributed in the interval $ ( 0 , 1 ) $. On the assumption that the $ a _ {n} $ are the values of a function defined on the infinite interval $ ( 1 , \infty ) $ and satisfying special analytic conditions, this theorem has a more precise version concerning the "quality" of the uniform distribution. J. Koksma [8] proved a general theorem on the distribution of the fractional parts (cf. Distribution modulo one) of a function in two variables $ f ( \alpha , n ) $, where $ \alpha $ is a real number taking almost-all values from the interval $ ( 1 , \infty ) $, and $ n = 1 , 2 , . . $. For example, the fractional parts $ \{ \alpha ^ {n} \} $, for almost-all $ \alpha > 1 $, are uniformly distributed in the interval $ ( 0 , 1 ) $.
Apart from questions connected with Borel normal numbers, one of the basic objects in metric number theory, from the start of its development, was the metric theory of continued fractions. Let $ \alpha $ be a real number in the interval $ ( 0 , 1 ) $, let $ \alpha = [ 0 , a _ {1} ,\dots ] $ be its continued fraction expansion, let $ r _ {n} ( \alpha ) = [ a _ {n} , a _ {n+} 1 ,\dots ] $, and let $ q _ {n} ( \alpha ) $ be the denominator of the $ n $- th convergent $ [ 0 , a _ {1} \dots a _ {n} ] $. A.Ya. Khinchin established (1935) that for almost-all $ \alpha $, as $ n \rightarrow \infty $,
$$ ( a _ {1} \dots a _ {n} ) ^ {1/n} \rightarrow K = \prod_{k=1}^ \infty \left ( 1 + \frac{1}{k ( k + 1 ) } \right ) ^ { \mathop{\rm ln} k / \mathop{\rm ln} 2 } = $$
$$ = \ 2 . 68545 \dots , $$
and there is an absolute constant $ \gamma $ such that for almost-all $ \alpha $, $ ( q _ {n} ( \alpha ) ) ^ {1/n} \rightarrow \gamma $ as $ n \rightarrow \infty $. P. Lévy found $ \gamma = \mathop{\rm exp} ( \pi ^ {2} / 12 \mathop{\rm ln} 2 ) $. In addition, Khinchin [5] used his results on the metric properties of continued fractions to prove a theorem on the approximation of numbers by rationals. Let $ f $ be a positive continuous function of a positive argument $ x $ such that $ x f ( x) $ is a non-increasing function. Then the inequality
$$ \tag{* } \left | \alpha - \frac{p}{q} \right | < f( \frac{q)}{q} $$
has, for almost-all $ \alpha $, an infinite set of solutions in integers $ p $ and $ q $( $ q > 0 $) if for some $ c > 0 $ the integral
$$ \int\limits _ { c } ^ \infty f ( x) d x $$
diverges; conversely, the inequality (*) has, for almost-all $ \alpha $, at most a finite number of solutions in integers $ p $ and $ q $( $ q > 0 $) if the integral converges for all $ c > 0 $.
This theorem has been transcended and generalized from various points of view. It became the starting point of an intensive development of the metric theory of Diophantine approximation. P. Erdös [7], completing a series of papers of his predecessors, obtained the following result. A necessary and sufficient condition under which for almost-all $ \alpha $ an infinite number of $ q _ {i} ( \alpha ) $ are contained in an arbitrary sequence $ n _ {1} < n _ {2} < \dots $ is
$$ \sum_{i=1}^ \infty \frac{\phi ( n _ {i} ) }{n _ {i} ^ {2} } = \infty , $$
where $ \phi ( n ) $ is the Euler function. Under the same condition, for almost-all $ \alpha $ the inequality
$$ \left | \alpha - \frac{m}{n _ {i} } \right | < \frac \epsilon {n _ {i} ^ {2} } ,\ \ ( m , n _ {i} ) = 1 , $$
where $ m $ is an integer and $ \epsilon > 0 $ is arbitrary, has an infinite number of solutions. These results are close to the conjecture (1982): If $ n _ {1} < n _ {2} \dots $ is an arbitrary sequence of integers and $ \delta _ {i} > 0 $ are arbitrary, then the inequality
$$ \left | \alpha - \frac{m}{n _ {i} } \right | < \ \frac{\delta _ {i} }{n _ {i} } ,\ ( m , n _ {i} ) = 1 , $$
has an infinite number of solutions for almost-all $ \alpha $ if and only if
$$ \sum_{i=1}^ \infty \frac{\delta _ {i} \phi ( n _ {i} ) }{n _ {i} } = \infty . $$
R.O. Kuz'min proved (1928) that for any $ x \in ( 0 , 1 ) $ the measure $ m _ {n} ( x ) $ of the set of $ \alpha $' s for which $ r _ {n} ( \alpha ) - a _ {n} < x $, is equal to
$$ \frac{ \mathop{\rm ln} ( 1 + x ) }{ \mathop{\rm ln} 2 } + O \left ( e ^ {- \lambda \sqrt n } \right ) , $$
where $ \lambda > 0 $ is an absolute constant. The asymptotic relation
$$ m _ {n} ( x ) \sim \ \frac{ \mathop{\rm ln} ( 1 + x ) }{ \mathop{\rm ln} 2 } \ \ ( n \rightarrow \infty ) $$
was known to C.F. Gauss, but he did not publish it, and he mentions in one of his letters to P. Laplace that it would be very desirable to estimate the difference $ m _ {n} ( x ) - \mathop{\rm ln} ( 1+ x ) / \mathop{\rm ln} 2 $. Kuz'min's estimate $ O ( e ^ {- \lambda \sqrt n } ) $ was improved by Lévy (1929) to $ O ( e ^ {- \lambda n } ) $. Kuz'min's method was the source of many other metric theorems on continued fractions.
The modern treatment of metric questions connected with Borel normal numbers and the theory of continued fractions uses ideas of ergodic theory. This is based on the fact that the mappings $ \alpha \rightarrow \{ \alpha g \} $ and $ \alpha \rightarrow \{ 1 / \alpha \} $ of the interval $ ( 0 , 1 ) $ into itself, which are closely connected with the $ g $- ary fraction and the continued fraction respectively, preserve a measure and are ergodic: the first preserves the Lebesgue measure, the second the measure $ \mu ( A ) $ defined for every measurable set $ A $ in $ ( 0 , 1 ) $ by
$$ \mu ( A ) = \ \frac{1}{ \mathop{\rm ln} 2 } \int\limits _ { A } \frac{dx}{1+} x . $$
From this point of view the Gauss–Kuz'min theorem, without estimates on the remainder, follows immediately from Birkhoff's individual ergodic theorem. Arguments from ergodic theory turn out to be useful even in order to obtain estimates of the remainder in certain limit theorems. For example, the results of Khinchin admit the improvement (see [10])
$$ ( a _ {1} \dots a _ {n} ) ^ {1/n} = \ K + O ( n ^ {- 1/2 } ( \mathop{\rm ln} n ) ^ {3/2 + \epsilon } ) $$
$$ ( q _ {n} ( \alpha ) ) ^ {1/n} = \mathop{\rm exp} \left ( \frac{\pi ^ {2}}{12 \mathop{\rm ln} 2 } \right ) + O ( n ^ {1/2} ( \mathop{\rm ln} n ) ^ {2 + \epsilon } ) , $$
where $ \epsilon > 0 $ is arbitrary. The ideas of ergodic theory are useful in many other problems of the metric theory of numbers (linear Diophantine equations, the distribution of values of matrix exponential functions, the Jacobi–Perron algorithm, and others).
In certain cases the metric characteristics of sets of numbers, based on the Lebesgue measure, turn out to be too coarse, and then more precise characteristics are used, for example, the Hausdorff dimension. Such an approach is particularly useful in the theory of Diophantine approximations and in the theory of transcendental numbers. For example, it has been shown [6] that for any fixed $ n $ and $ w \geq n+ 1 $ the set of real numbers $ x $ for which the inequality
$$ | x - a | < h _ \alpha ^ {-} w $$
has an infinite number of solutions in algebraic numbers $ \alpha $ of degree $ n $ and height $ h _ \alpha $, has Hausdorff dimension $ ( n+ 1 ) / w $. If $ w < ( n+ 1 ) $, then the corresponding inequality has an infinite number of solutions for almost-all $ x $, at the same time it has been suggested that this is true for all $ x $( Wirsing's conjecture). Similar results are known for complex numbers. They are directly related to the fundamental classification questions for transcendental numbers [3].
From the metric point of view, not only problems concerning real and complex numbers have been analyzed, but also problems on $ p $- adic numbers, adèles, formal power series, etc., and, in general, elements of arbitrary spaces in which a measure can be introduced and in which some "arithmetic" problem can be posed. In particular, for $ p $- adic numbers there are analogues of many metric theorems from the theory of uniform distribution and the theory of Diophantine approximations of real numbers, despite the fact that the domain of $ p $- adic numbers differs in its metric and topology (see [3], [9]).
The metric approach is effective for the solution of "ill-posed" problems, when shortage of information on the object of research is compensated by the assumption of a "random" choice of this object from some suitable set of objects. Here, of course, one will not succeed in investigating the primary object, which is sometimes essentially impossible because of lack of information concerning it, but one may conclude that "almost-all" objects of the set considered have a certain property. For example, let $ A ^ {*} = \{ 1 < a _ {1} ^ {*} < a _ {2} ^ {*} < \dots \} $ be a sequence of natural numbers increasing less rapidly than some power, that is, $ a _ {i} ^ {*} < i ^ \mu $, $ \mu $ a constant. One poses the question: Does there exist a number $ r $ such that any natural number can be represented as a sum of at most $ r $ terms of $ A ^ {*} $? Clearly, the information given on $ A ^ {*} $ is not sufficient to solve this problem.
Let $ \mathfrak A $ be the set of sequences $ A = \{ 1 < a _ {1} < a _ {2} < \dots \} $ of integers, where each $ a _ {i} $ is "randomly" chosen from the interval $ [ a _ {i} ^ {*} , a _ {i+} 1 ^ {*} ) $. Lebesgue measure can be defined on $ \mathfrak A $ and it can be proved that for almost-all $ A $ the required number exists and that $ r < \infty $( see [4]).
The connection between "global" results in the metric theory of numbers and their "individual" realizations is very interesting and profound. Despite the fact that almost-all elements of some set have a given property, it can be very difficult to establish that a given concrete element of the set has the property. For example, Borel conjectured that numbers such as $ \sqrt 2 $, $ e $, $ \pi $, $ \mathop{\rm log} 3 $, etc., are normal; and, although almost-all numbers are normal, up till now (1989) it is not known whether any of these numbers is normal. In many cases it is easier to prove a metric theorem than to prove a similar "individual" theorem. However, this does not mean that there are no deep problems in the metric theory of numbers, since many problems in the metric theory of numbers are closely connected with certain "individual" problems which are sometimes discovered fairly quickly. On the other hand, the solution of "individual" problems reveals their relationship to the metric problems.
The ideas of the metric theory of numbers play a fundamental role in many areas of analytic number theory, in particular when integration with respect to some measure is involved. In these cases the conclusions of certain metric theorems may not be the aim of research, but the metric understanding is used as an intermediate stage in the arguments. These theorems may be a main principle underlying the arguments; however, the final formulation of the result will not contain any metric notions. An example of the systematic use of this type of argument is the Hardy–Littlewood–Vinogradov method, in which an essential role is played by metric properties of approximations of numbers by rational fractions (the "major" and "minor" arcs of Hardy–Littlewood). This situation allowed I.M. Vinogradov to formulate his own theorems on estimates of Weyl sums as certain metric theorems [1]. In addition, Vinogradov's method of estimating Weyl sums has a clearly expressed metric character, establishing a connection between the "global" estimate of the integral and the "individual" estimate of a concrete sum. Examples of this type are rare in number theory.
References
| [1] | I.M. Vinogradov, "The method of trigonometric sums in the theory of numbers" , Interscience (1954) (Translated from Russian) |
| [2] | A.G. Postnikov, "Ergodic problems in the theory of congruences and of Diophantine approximations" , Amer. Math. Soc. (1967) (Translated from Russian) |
| [3] | V.G. Sprindzhuk, "Mahler's problem in metric number theory" , Amer. Math. Soc. (1969) (Translated from Russian) |
| [4] | V.G. Sprindzhuk, "Ueber die Darstellung ganzer Zahlen durch eine beschränkte Zahl von Zufälligen Summanden" Izv. Akad. Nauk BSSR Ser. Fiz. Mat. Nauk , 1 (1970) pp. 5–14 |
| [5] | A.Ya. Khinchin, "Continued fractions" , Univ. Chicago Press (1964) (Translated from Russian) |
| [6] | A. Baker, W. Schmidt, "Diophantine approximation and Hausdorff dimension" Proc. London Math. Soc. (3) , 21 (1970) pp. 1–11 |
| [7] | P. Erdös, "On the distribution of the convergents of almost all real numbers" J. Number Theory , 2 (1970) pp. 425–441 |
| [8] | J.F. Koksma, "Diophantische Approximationen" , Springer (1936) |
| [9] | E. Lutz, "Sur les approximations diophantiennes linéaires 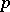 -adiques" , Hermann (1955) -adiques" , Hermann (1955) |
| [10] | W. Philipp, "Some metrical theorems in number theory" Pacific J. Math. , 20 : 1 (1967) pp. 109–127 |
| [11] | J. Cigler, G. Helmberg, "Neuere Entwicklungen der Theorie der Gleichverteilung" Jhber. Deutsch. Math. Verein. , 64 : 1 (1961) pp. 1–50 |
Comments
For a number of striking applications of measure-theoretic and ergodic-theoretic ideas in number theory see also [a1].
References
| [a1] | H. Furstenberg, "Recurrence in ergodic theory and combinatorial number theory" , Princeton Univ. Press (1981) |
Metric theory of numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Metric_theory_of_numbers&oldid=55100